1.1.2 等腰三角形(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 1.1.2 等腰三角形(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 506.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 15:38:07 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学下册第1章三角形的证明
1.1
等腰三角形
第2课时
等腰三角形2
【知识清单】
1.等腰三角形两底角平分线相等,两腰上的中线、高也相等.
2.等边三角形的三个内角都相等,并且每一个角都等于60°.
【经典例题】
例题1、如图,△ABC中,AC=AD,BC=BE,∠ACB=126°,则∠ECD=( )
A.
23°
B.
25°
C.
27°
D.31°
【考点】等腰三角形的性质.
【分析】根据AC=AD,BC=BE,利用等腰三角形的性质,可得∠ACD=∠ADC
∠BCE=∠BEC.再利用三角形内角和定理可得∠A+∠B+∠ACB=180°,∠ACB=126°,可得∠A+∠B=54°,进而可以求得∠ECD+∠CDE
=153°,再由∠ECD+∠CDE
+∠ECD=180°,可得∠DCE的大小.
【解答】∵
AC=AD,
BC=BE,
∴
∠ACD=∠ADC
,∠BCE=∠BEC.
而在△ABC中,∠ACB=126°,
∴∠A+∠B=180°-116°=54°,
又在△ACD中,
∠ACD+∠ADC=180°-∠A,
在△BCE中,
∠BCE+∠BEC=180°-∠B,
∴∠BCE+∠BEC+∠ACD+∠ADC=360°-54°=306°,
∴2∠BEC+2∠ADC=306°,
∴∠BEC+∠ADC=153°,
∴在△ECD中,
∠ECD=180°-(∠ECD+∠CDE)=180°-(∠BCE+∠ADC)
=180°-153°
=27°.
故选C.
【点评】本题考查了等腰三角形的性质、三角形内角和定理.解答此题的关键是建立起各角之间的等量关系,结合图形列出相关等式进行解答即可.
例题2、如图,已知△ABC和△BDE都是等边三角形,求证:AE=CD.
【考点】?等边三角形的性质;全等三角形的判定与性质.
【分析】根据等边三角形各边长相等的性质,可得AB=BC,BE=BD,根据等边三角形各内角为60°,可得∠ABE=∠DBE,进而求证△ABE≌△CBD(SAS),即可求得AE=CD.
【解答】证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE=60°
又∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠ABE=∠DBE,
∴在△ABE和△CBD中,
∵,
∴△ABE≌△CBD(SAS),
∴AE=CD.
【点评】本题考查了全等三角形的证明,全等三角形对应边相等的性质,等边三角形各内角为60°的性质,本题中求证△ABE≌△CBD(SAS)是解题的关键.
【夯实基础】
1、下列命题:①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等;③等腰三角形的最短边是底边;④等边三角形的高、中线、角平分线都相等;⑤等腰三角形都是锐角三角形.其中不正确的有(?
)?
A.1个
B.2个
C.3个
D.4个
2、如图,将边长为5个单位的等边△ABC沿边BC向右平移4个单位得到△,则四边形的周长为( )
A.28
B.26
C.24
D.23
3、如图,直线l∥m∥n,等边三角形ABC的顶点A,B,C分别在直线m、l和n上,边AC与直线m的夹角为38°,则∠α的度数为( )
A.22°
B.24°
C.28°
D.38°
4、若a、b为实数,且满足=0
,以a、b的值为两边长的等腰三角形的面积是(
)
A.120
B.60
C.40
D.30
5、边长为12cm的等边三角形的面积为=
.
6、等腰三角形的周长为17,且三边均为整数,则腰长为
.
7、等腰三角形一腰上的高与腰的夹角为50°,则这个等腰三角形的顶角是
.
8、如图已知CA=CD,EA=EB,∠CFE=123°,求∠A的度数.
9、如图,
△ABC是等边三角形,E、D分别是边BC,AC上的点,且BE=CD,
求证:∠AEC+∠BDC=180°.
【提优特训】
10、等腰三角形两腰上的高相交所成的钝角为100°,则顶角的度数为
(
).
A.80°
B.100°
C.80或100°
D.80°或140°
11、如图,点D是△ABC内一点,AD=BD=CD,若∠BAC=62°,则∠DBC度数是(
)
A.28°
B.32°
C.36°
D.40°
12、如图,△ABC中,AB=AC,△DEF为等边三角形,则α、β、γ之间的关系为(
)
A.2β=
α+γ
B.2α=β+γ
C.2β=
α-γ
D.2α=β-γ
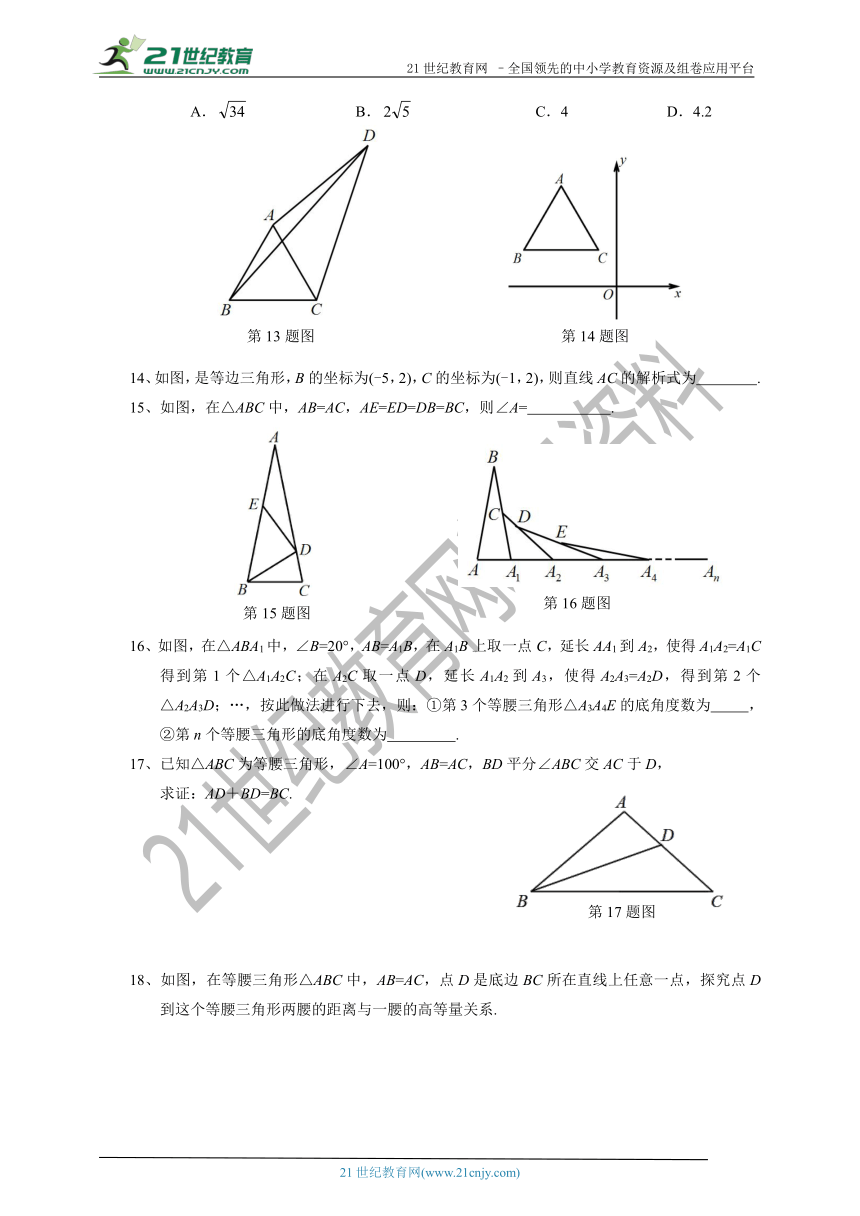
13、如图,四边形ABCD中,AC、BD为对角线,△ABC为等边三角形,∠ADC=30°,AD=3,BD=5,则CD的长为
(
).
A.
B.
C.4
D.4.2
14、如图,是等边三角形,B的坐标为(-5,2),C的坐标为(-1,2),则直线AC的解析式为
.
15、如图,在△ABC中,AB=AC,AE=ED=DB=BC,则∠A=
.
16、如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C得到第1个△A1A2C;在A2C取一点D,延长A1A2到A3,使得A2A3=A2D,得到第2个△A2A3D;…,按此做法进行下去,则:①第3个等腰三角形△A3A4E的底角度数为
,
②第n个等腰三角形的底角度数为
.
17、已知△ABC为等腰三角形,∠A=100°,AB=AC,BD平分∠ABC交AC于D,
求证:AD+BD=BC.
18、如图,在等腰三角形△ABC中,AB=AC,点D是底边BC所在直线上任意一点,探究点D到这个等腰三角形两腰的距离与一腰的高等量关系.
【中考链接】
19、(2020?江苏苏州)
如图,在△ABC中,BAC108,将△ABC绕点A按逆时针方向旋转得到△ABC.若点B恰好落在BC边上,且ABCB,则C的度数为(
).
A.18°
B.20°
C.24°
D.28°
20、(2020?西藏)如图,△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
参考答案
1、C
2、D
3、A
4、B
5、cm2
6、5或6或7或8
7、40°或140°
10、C
11、A
12、B
13、C
14、
15、
16、①10°
②
19、C
8、如图已知,
CA=CD,EA=EB,∠CFE=123°,求∠A的度数.
解: ∵CA=CD,EA=EB,
∴∠A=∠ADC,∠A=∠ABE,
在△ACD中,∠C+∠A+∠ADC=180°,
即∠C+2∠A
=180°,
∴∠C
=180°-2∠A,
同理∠E
=180°-2∠A.
∵∠CFE=∠FDE+∠E,∠FDE=∠A+∠C,
∴∠CFE=∠A+∠C+∠E.
∴∠CFE=∠A+180°-2∠A
+180°-2∠A.
∵∠CFE=123°,
∴123°=∠A+180°-2∠A
+180°-2∠A.
解得∠A=79°.
9、如图,
△ABC是等边三角形,E、D分别是边BC,AC上的点,且BE=CD,
求证:∠AEC+∠BDC=180°.
证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠ABC=∠C=60°.
在△ABE和△BCD中,
∵,
∴△ABE≌△BCD(SAS).
∴∠1=∠2,
∵∠APD=∠1+∠ABP=∠2+∠ABP=∠ABC=60°,
∴∠DPE=120°,
∵∠C+∠DPE=60°+120°=180°,
∴∠AEC+∠BDC=360°-
(∠C+∠DPE)=360°-180°=180°.
17、已知△ABC为等腰三角形,∠A=100°,AB=AC,BD平分∠ABC交AC于D,
求证:AD+BD=BC.
证明:如图,在BC上截取BE=BA,延长BD到F使BF=BC,连接DE、CF.
∵AB=AC,
∴∠1=∠2=,
在△ABD和△EBD中,
∵,
∴△ABD≌△EBD.
∴∠DEB=∠A=100°,则∠5=∠DEC=80°.
∵AB=AC,
∴∠ABC=∠6==40°,
∴∠3=180°∠5∠6=60°,
∴∠4=∠ADB=180°∠A∠1=60°,
∴∠3=∠4,
∵BC=BF,∠2=20°,
∴∠F=∠FCB=,
∴∠5=∠F,
又∵DC=DC,
在△CED和△CFD中,
∵,
∴△CED≌△CFD(AAS),
∴DF=DE=AD,
∴BC=BF=BD+DF=BD+AD.
18、如图,在等腰三角形△ABC中,AB=AC,点D是底边BC所在直线上任意一点,探究点D到这个等腰三角形两腰的距离与一腰的高等量关系.
探究:(1)如图1,点D在底边BC上(不与B、C重合),DE⊥AB于E,DF⊥AC于F,CG⊥AB于G,则DE+DF=CG;
如图1,连接AD,则S△ABC=S△ABD+S△ACD,
∴.
∵AB=AC,
∴CG=DE+DF;
探究(2)如图2,点D在直线BC上点C的右侧,DE⊥AB于E,DF⊥AC于F,CG⊥AB于G,则DEDF=CG;
如图2,连接AD,则S△ABC=S△ABDS△ACD,
∴
∵AB=AC,
∴;
探究(3)如图3,点D在直线BC上点B的左侧,DE⊥AB于E,DF⊥AC于F,CG⊥AB于G,则DFDE=CG.
如图3,连接AD,则S△ABC=S△ADCS△ADB,
∴
∵AB=AC,
∴.
20、(2020?西藏)如图,△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
证明:∵∠BAE=∠CAD,
∴∠BAE+∠BAD=∠CAD+∠BAD,
∴∠EAD=∠BAC.
在△EAD和△BAC中,
∵,
∴△EAD≌△BAC(SAS),
∴DE=CB.
第3题图
例题1图
例题2图
第2题图
第13题图
第9题图
第20题图
第8题图
第17题图
第19题图
第16题图
第15题图
第11题图
第14题图
第18题图3
第18题图2
第12题图
第18题图1
第18题图1
第17题图
第17题图
第9题图
第8题图
第20题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学下册第1章三角形的证明
1.1
等腰三角形
第2课时
等腰三角形2
【知识清单】
1.等腰三角形两底角平分线相等,两腰上的中线、高也相等.
2.等边三角形的三个内角都相等,并且每一个角都等于60°.
【经典例题】
例题1、如图,△ABC中,AC=AD,BC=BE,∠ACB=126°,则∠ECD=( )
A.
23°
B.
25°
C.
27°
D.31°
【考点】等腰三角形的性质.
【分析】根据AC=AD,BC=BE,利用等腰三角形的性质,可得∠ACD=∠ADC
∠BCE=∠BEC.再利用三角形内角和定理可得∠A+∠B+∠ACB=180°,∠ACB=126°,可得∠A+∠B=54°,进而可以求得∠ECD+∠CDE
=153°,再由∠ECD+∠CDE
+∠ECD=180°,可得∠DCE的大小.
【解答】∵
AC=AD,
BC=BE,
∴
∠ACD=∠ADC
,∠BCE=∠BEC.
而在△ABC中,∠ACB=126°,
∴∠A+∠B=180°-116°=54°,
又在△ACD中,
∠ACD+∠ADC=180°-∠A,
在△BCE中,
∠BCE+∠BEC=180°-∠B,
∴∠BCE+∠BEC+∠ACD+∠ADC=360°-54°=306°,
∴2∠BEC+2∠ADC=306°,
∴∠BEC+∠ADC=153°,
∴在△ECD中,
∠ECD=180°-(∠ECD+∠CDE)=180°-(∠BCE+∠ADC)
=180°-153°
=27°.
故选C.
【点评】本题考查了等腰三角形的性质、三角形内角和定理.解答此题的关键是建立起各角之间的等量关系,结合图形列出相关等式进行解答即可.
例题2、如图,已知△ABC和△BDE都是等边三角形,求证:AE=CD.
【考点】?等边三角形的性质;全等三角形的判定与性质.
【分析】根据等边三角形各边长相等的性质,可得AB=BC,BE=BD,根据等边三角形各内角为60°,可得∠ABE=∠DBE,进而求证△ABE≌△CBD(SAS),即可求得AE=CD.
【解答】证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE=60°
又∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠ABE=∠DBE,
∴在△ABE和△CBD中,
∵,
∴△ABE≌△CBD(SAS),
∴AE=CD.
【点评】本题考查了全等三角形的证明,全等三角形对应边相等的性质,等边三角形各内角为60°的性质,本题中求证△ABE≌△CBD(SAS)是解题的关键.
【夯实基础】
1、下列命题:①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等;③等腰三角形的最短边是底边;④等边三角形的高、中线、角平分线都相等;⑤等腰三角形都是锐角三角形.其中不正确的有(?
)?
A.1个
B.2个
C.3个
D.4个
2、如图,将边长为5个单位的等边△ABC沿边BC向右平移4个单位得到△,则四边形的周长为( )
A.28
B.26
C.24
D.23
3、如图,直线l∥m∥n,等边三角形ABC的顶点A,B,C分别在直线m、l和n上,边AC与直线m的夹角为38°,则∠α的度数为( )
A.22°
B.24°
C.28°
D.38°
4、若a、b为实数,且满足=0
,以a、b的值为两边长的等腰三角形的面积是(
)
A.120
B.60
C.40
D.30
5、边长为12cm的等边三角形的面积为=
.
6、等腰三角形的周长为17,且三边均为整数,则腰长为
.
7、等腰三角形一腰上的高与腰的夹角为50°,则这个等腰三角形的顶角是
.
8、如图已知CA=CD,EA=EB,∠CFE=123°,求∠A的度数.
9、如图,
△ABC是等边三角形,E、D分别是边BC,AC上的点,且BE=CD,
求证:∠AEC+∠BDC=180°.
【提优特训】
10、等腰三角形两腰上的高相交所成的钝角为100°,则顶角的度数为
(
).
A.80°
B.100°
C.80或100°
D.80°或140°
11、如图,点D是△ABC内一点,AD=BD=CD,若∠BAC=62°,则∠DBC度数是(
)
A.28°
B.32°
C.36°
D.40°
12、如图,△ABC中,AB=AC,△DEF为等边三角形,则α、β、γ之间的关系为(
)
A.2β=
α+γ
B.2α=β+γ
C.2β=
α-γ
D.2α=β-γ
13、如图,四边形ABCD中,AC、BD为对角线,△ABC为等边三角形,∠ADC=30°,AD=3,BD=5,则CD的长为
(
).
A.
B.
C.4
D.4.2
14、如图,是等边三角形,B的坐标为(-5,2),C的坐标为(-1,2),则直线AC的解析式为
.
15、如图,在△ABC中,AB=AC,AE=ED=DB=BC,则∠A=
.
16、如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C得到第1个△A1A2C;在A2C取一点D,延长A1A2到A3,使得A2A3=A2D,得到第2个△A2A3D;…,按此做法进行下去,则:①第3个等腰三角形△A3A4E的底角度数为
,
②第n个等腰三角形的底角度数为
.
17、已知△ABC为等腰三角形,∠A=100°,AB=AC,BD平分∠ABC交AC于D,
求证:AD+BD=BC.
18、如图,在等腰三角形△ABC中,AB=AC,点D是底边BC所在直线上任意一点,探究点D到这个等腰三角形两腰的距离与一腰的高等量关系.
【中考链接】
19、(2020?江苏苏州)
如图,在△ABC中,BAC108,将△ABC绕点A按逆时针方向旋转得到△ABC.若点B恰好落在BC边上,且ABCB,则C的度数为(
).
A.18°
B.20°
C.24°
D.28°
20、(2020?西藏)如图,△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
参考答案
1、C
2、D
3、A
4、B
5、cm2
6、5或6或7或8
7、40°或140°
10、C
11、A
12、B
13、C
14、
15、
16、①10°
②
19、C
8、如图已知,
CA=CD,EA=EB,∠CFE=123°,求∠A的度数.
解: ∵CA=CD,EA=EB,
∴∠A=∠ADC,∠A=∠ABE,
在△ACD中,∠C+∠A+∠ADC=180°,
即∠C+2∠A
=180°,
∴∠C
=180°-2∠A,
同理∠E
=180°-2∠A.
∵∠CFE=∠FDE+∠E,∠FDE=∠A+∠C,
∴∠CFE=∠A+∠C+∠E.
∴∠CFE=∠A+180°-2∠A
+180°-2∠A.
∵∠CFE=123°,
∴123°=∠A+180°-2∠A
+180°-2∠A.
解得∠A=79°.
9、如图,
△ABC是等边三角形,E、D分别是边BC,AC上的点,且BE=CD,
求证:∠AEC+∠BDC=180°.
证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠ABC=∠C=60°.
在△ABE和△BCD中,
∵,
∴△ABE≌△BCD(SAS).
∴∠1=∠2,
∵∠APD=∠1+∠ABP=∠2+∠ABP=∠ABC=60°,
∴∠DPE=120°,
∵∠C+∠DPE=60°+120°=180°,
∴∠AEC+∠BDC=360°-
(∠C+∠DPE)=360°-180°=180°.
17、已知△ABC为等腰三角形,∠A=100°,AB=AC,BD平分∠ABC交AC于D,
求证:AD+BD=BC.
证明:如图,在BC上截取BE=BA,延长BD到F使BF=BC,连接DE、CF.
∵AB=AC,
∴∠1=∠2=,
在△ABD和△EBD中,
∵,
∴△ABD≌△EBD.
∴∠DEB=∠A=100°,则∠5=∠DEC=80°.
∵AB=AC,
∴∠ABC=∠6==40°,
∴∠3=180°∠5∠6=60°,
∴∠4=∠ADB=180°∠A∠1=60°,
∴∠3=∠4,
∵BC=BF,∠2=20°,
∴∠F=∠FCB=,
∴∠5=∠F,
又∵DC=DC,
在△CED和△CFD中,
∵,
∴△CED≌△CFD(AAS),
∴DF=DE=AD,
∴BC=BF=BD+DF=BD+AD.
18、如图,在等腰三角形△ABC中,AB=AC,点D是底边BC所在直线上任意一点,探究点D到这个等腰三角形两腰的距离与一腰的高等量关系.
探究:(1)如图1,点D在底边BC上(不与B、C重合),DE⊥AB于E,DF⊥AC于F,CG⊥AB于G,则DE+DF=CG;
如图1,连接AD,则S△ABC=S△ABD+S△ACD,
∴.
∵AB=AC,
∴CG=DE+DF;
探究(2)如图2,点D在直线BC上点C的右侧,DE⊥AB于E,DF⊥AC于F,CG⊥AB于G,则DEDF=CG;
如图2,连接AD,则S△ABC=S△ABDS△ACD,
∴
∵AB=AC,
∴;
探究(3)如图3,点D在直线BC上点B的左侧,DE⊥AB于E,DF⊥AC于F,CG⊥AB于G,则DFDE=CG.
如图3,连接AD,则S△ABC=S△ADCS△ADB,
∴
∵AB=AC,
∴.
20、(2020?西藏)如图,△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
证明:∵∠BAE=∠CAD,
∴∠BAE+∠BAD=∠CAD+∠BAD,
∴∠EAD=∠BAC.
在△EAD和△BAC中,
∵,
∴△EAD≌△BAC(SAS),
∴DE=CB.
第3题图
例题1图
例题2图
第2题图
第13题图
第9题图
第20题图
第8题图
第17题图
第19题图
第16题图
第15题图
第11题图
第14题图
第18题图3
第18题图2
第12题图
第18题图1
第18题图1
第17题图
第17题图
第9题图
第8题图
第20题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
