人教版数学九年级下册第二十七章《相似》单元基础提升训练卷(Word版 含答案)
文档属性
| 名称 | 人教版数学九年级下册第二十七章《相似》单元基础提升训练卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1019.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 13:00:48 | ||
图片预览

文档简介
九年级人教版数学下册第二十七章《相似》单元基础提升训练卷
一、单选题
1.观察下列每组图形,相似图形是( )
A. B.
C. D.
2.下列说法中,正确的是( )
A.两个矩形必相似 B.两个含角的等腰三角形必相似
C.两个菱形必相似 D.两个含角的直角三角形必相似
3.如图,已知,那么添加下列一个条件后,仍然无法判定的是( )
A. B. C. D.
4.如图,是的中位线,,则S四边形DBCE的面积是( )
A.4 B.6 C.2 D.5
5.如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底()7.8米的点处,然后观察者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得米,观察者目高米,则树()的高度约为( )米.
A.15.6 B.6.4 C.3.4 D.3.9
6.如图,在平面直角坐标系中,已知与是位似图形,原点是位似中心,位似比,若,则的长为( ).
A.5 B.6 C.9 D.12
7.如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且,已知DE:DF=3:7,BC=14,则AB的长为( )
A.10.5 B.6 C.7 D.8
8.如图,已知BD与CE相交于点A,DE∥BC,如果AD=2,AB=3,AC=6,那么AE等于( )
A. B. C.4 D.9
9.如图,已知边长为的正方形,是的中点,是的中点,与相交于,和相交于.则四边形的面积为( )
A. B. C. D.
10.如图,在中,点在边上,,,联结,与相交于点,则下列结论一定正确的是( )
A. B. C. D.
11.如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是( )
A.△AOM和△AON都是等边三角形
B.四边形MBON和四边形MODN都是菱形
C.四边形AMON与四边形ABCD是位似图形
D.MO∥BC且BM=CO
12.如图,正方形的对角线,交于点,的平分线交于,交于,且.下列结论中:①;②;③若,则的长为.其中正确的结论有( )
A.①② B.①③ C.②③ D.①②③
二、填空题
13.已知点P是线段AB的一个黄金分割点,且AP>BP,那么AP:AB的比值为______.
14.如图,已知AD,要使ABC∽DEF,还需添加一个条件,你添加的条件是____.(只需写一个条件,不添加辅助线和字母)
15.如图:在中,,,,则________.
16.如图,△ABC是等边三角形,AB=6.点D和E分别在边BC和AC上,且∠ADE=60°,BD=2,则CE的长为_____.
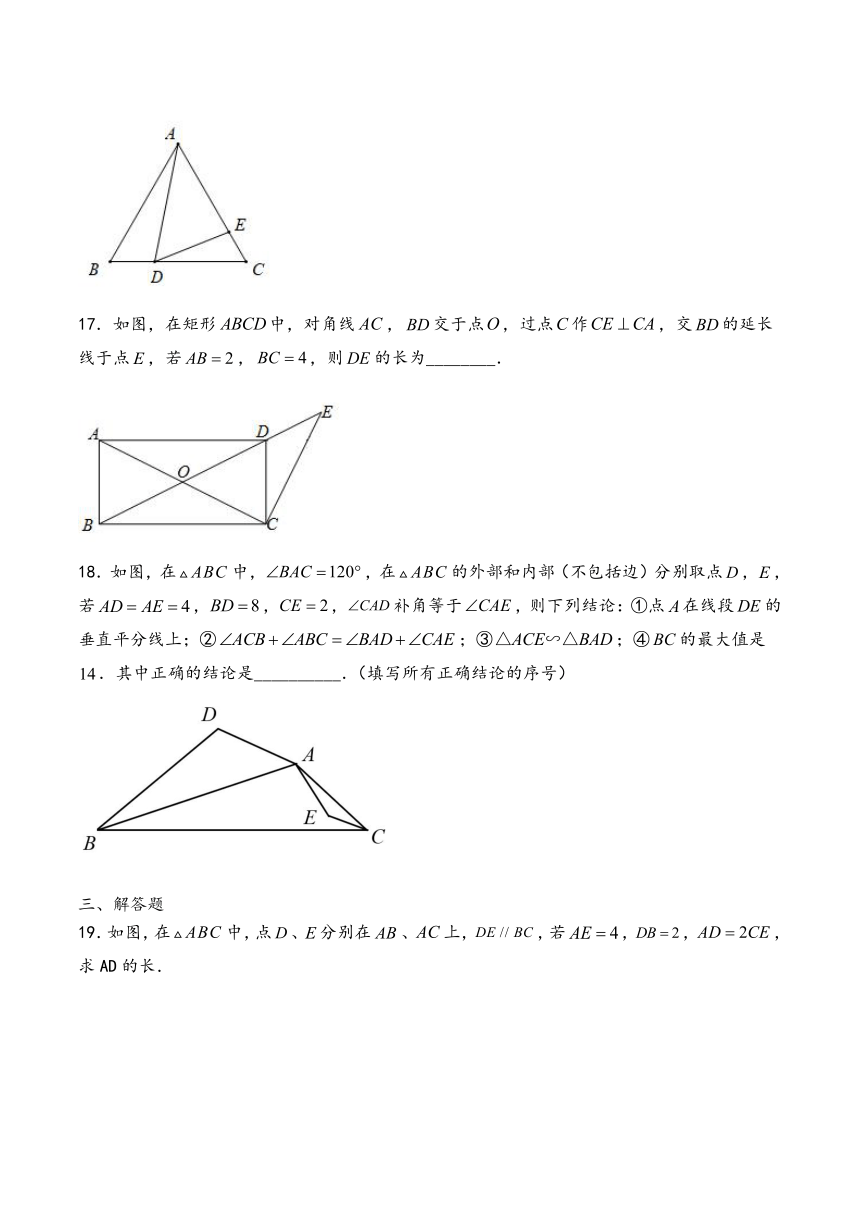
17.如图,在矩形中,对角线,交于点,过点作,交的延长线于点,若,,则的长为________.
18.如图,在中,,在的外部和内部(不包括边)分别取点,,若,,,补角等于,则下列结论:①点在线段的垂直平分线上;②;③;④的最大值是.其中正确的结论是__________.(填写所有正确结论的序号)
三、解答题
19.如图,在中,点、分别在、上,,若,,,求AD的长.
20.如图,在中,点D,E分别在边AB,AC上,连接DE,且.
(1)求证:ADE∽ACB;
(2)若∠B=55°,∠ADE =75°,求∠A的度数.
21.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
①计算小亮在路灯D下的影长;
②计算建筑物AD的高.
22.如图,AB是OO的直径,点D在AB的延长线上,C、E是OO上的两点,C为弧BE的中点,∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是OO的切线:
(2)求证:CE=CF:
(3)若BD=1,CD=,求弦AC的长.
23.如图,已知在菱形ABCD中,对角线AC、BD相交于点O,将△COD绕点O逆时针方向旋转得到△C1OD1,旋转角0°α90°,连结DD1、AC1、BD1,AC1与BD1相交于点P.
(1)判断△BDD1形状,并说明理由;
(2)①求证:;
②判断AC1与BD1的位置关系,并说明理由.
24.如图,为的直径,为延长线上一点,且,,为的弦,连接,连接并延长交于点,连接交于点.
(1)求证:直线是的切线;
(2)求的半径的长;
(3)求线段的长.
25.从三角形(不是等腰三角形)一个顶点引一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在中,,是的完美分割线,且,求的度数.
(2)如图2,在中,,,是的完美分割线,且是以为底边的等腰三角形,找出与的关系.
参考答案
1.C
解:A、两图形形状不同,故不是相似图形;
B、两图形形状不同,故不是相似图形;
C、两图形形状相同,故是相似图形;
D、两图形形状不同,故不是相似图形;
2.D
A、两个矩形的对应角相等,但对应边不一定成比例,则不一定相似,此项错误;
B、如果一个等腰三角形的顶角是,另一等腰三角形的底角是,则不相似,此项错误;
C、两个菱形的对应边成比例,但四个内角不一定对应相等,则不一定相似,此项错误;
D、两个含角的直角三角形必相似,此项正确;
3.B
解:∵∠DAB=∠CAE,
∴∠DAE=∠BAC,
A、若,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项A不符合题意;
B、若,且∠DAE=∠BAC,无法判定△ABC∽△ADE,故选项B符合题意;
C、若∠B=∠D,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项C不符合题意;
D、若∠C=∠AED,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项D不符合题意;
4.B
解:∵DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,
S△ADE:S△ABC=()2=,
又△ADE的面积是2,
∴△ABC的面积为8,
∴四边形DBCE的面积是8-2=6.
故选:B.
5.D
∵∠AEB=∠CED,∠BAE=∠DCE,
∴RtABE∽RtCDE,
∴,
即,
∴=3.9,
6.C
解:∵△ABC与△DEF是位似图形,
∴AB∥DE,
∴△OAB∽△ODE,
∴,即,
解得:DE=9,
7.A
设AB=x,根据题意得,
8.C
解:∵ED∥BC,
∴ ,
即,
∴AE=4,
9.C
解:∵正方形
∴BC∥AD,AD=BC=AB=2
∵是的中点,
∴
∴△BFH∽△DAH,
∴相似比为
∴△BFH与△DAH相似比为1:2,
∴△BFH与△DAH对应高的比1:2,
∴△BFH的BF边上的高为,△DAH的AD边上的高为,
∴△ADH的面积为,△FBH的面积为;
∵是的中点,
∴
∴
在△ABF和△DAE中
∵
∴△ABF≌△DAE,(SAS)
∴∠BAF=∠ADE,AF=DE
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,
∴∠AIE=90°=∠DAB,
∵∠ADE=∠IDA
∴△AEI∽△EDA,
∴
∵AF=DE=
∴
∴
∴△AEI的面积=
∴四边形BEIH的面积=
10.C
解:∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DE=CF,DF=CE,
∵DE∥BC,DF∥AC,
∴△ADE∽△ABC,△BFD∽△BAC,
∴,故A错误;
,即,故B错误;
∵DF∥AC,∴,故C正确;
∵DE∥BC,∴,故D错误,
11.C
解:∵∠BAD不一定等于为120°,
∴△AOM和△AON不一定都是等边三角形,A错误;
∵BM不一定等于BO,
∴四边形MBON和四边形MODN不一定都是菱形,B错误;
∵四边形ABCD为菱形,
∴AO=OC,又AM=MB,
∴OM∥BC,OM=BC,
同理,ON∥CD,ON=CD,
∴四边形AMON与四边形ABCD是以A为位似中心的位似图形,C正确;
MO∥BC,但BM不一定等于CO,D错误;
故选:C.
12.D
(1)延长DG、BC交于点H,
∵BG平分∠CBD,
∴∠1=∠2,
∵DG⊥BG,
∴∠BGD=∠BGH=90°,
又∵BG=BG,
∴△BGD≌△BGH(ASA),
∴BD=BH,
∴DH=2DG,
∵四边形ABCD是正方形,
∴BC=DC,∠BCF=∠DCH=90°,
又∵∠BGD=90°,∠3=∠4,
∴∠2=∠5,
∴△BCF≌△DCH(ASA),
∴BF=DH,
∴BF=2DG;①正确;
∵四边形ABCD是正方形,
∴∠ACB=∠BDC=45°,
∴∠BCE=∠BDF,
又∵∠1=∠2,
∴△BEC∽△BFD,②正确
∵BC=CD,BC2+CD2=BD2,
∴BD=BC
∴,
∵,
∴BF=.③正确
故选D.
13.
∵点P是线段的一个黄金分割点,且,
∴AP:AB=.
14.AB∥DE
∵∠A=∠D,
∴当∠B=∠DEF时,△ABC∽△DEF,
∵AB∥DE时,∠B=∠DEF,
∴添加AB∥DE时,使△ABC∽△DEF.
故答案为:AB∥DE.
15.9
∵,
∴△ADE∽△ABC,
∴相似比=,
∵,,
∴AB=AD+BD=3,
∴,
∴,
故答案为:9.
16..
∵△ABC是等边三角形,
∴∠B=∠C=60?,AB=BC=6,
∴∠BAD+∠ADB=180?-∠B=180?-60?=120?,
∵∠ADE=60°,
∴∠ADB+∠EDC=180?-∠ADE=180?-60?=120?,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴,
∵BD=2,
∴CD=BC-BD=6-2=4,
∴,
∴,
故答案为:.
17.
如图所示,作DF⊥AC于F点,
在Rt△ABC中,,,
根据矩形的性质可得:∠BAC=∠FCD,,
∴△ABC∽△CFD,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
故答案为:.
18.①②
∵AD=AE=4,
∴点A在线段DE的垂直平分线上;故①正确;
如图,延长DA至F,则∠CAF+∠CAD=180°,
∵∠BAC=120°,
∴∠ACB+∠ABC=60°,∠BAD+∠CAF=60°,
∵补角等于,
∴∠CAE=∠CAF,
∴∠ACB+∠ABC=∠BAD+∠CAE,故②正确,
∵,,,
∴=2,
∵不能证明∠ADB=∠CEA,
∴不能判定△ACE∽△BAD,故③错误,
∵2<AC<6,4<AB<12,
∴6<BC<18,
∴不能确定BC的最大值;故④错误;
综上所述:正确的结论为①②,
19.AD=4
解:∵DE∥BC,
∴,
设AD=x,则,
∴,
解得:x=4或﹣4(舍去),
即AD=4.
20.
(1)证明:∵,
∴.
又∵∠A=∠A,
∴△ADE∽△ACB;
(2)解:∵△ADE∽△ACB,
∴∠ADE=∠ACB,
∵∠ADE=75°,∴∠ACB=75°.
又∵∠B=55°,
∴∠A=180°-∠ACB-∠B=50°.
21.①1.5米 ②12米
①∵
∴ ,
,
∴ ,
∴AB=10,
∴BQ = 10- 2- 6.5= 1.5,
即小亮在路灯D下的影长是1.5米.
②∵
∴,
∴ ,
,
∴ ,
解得DA=12,
∴建筑物的高为12米.
22.
(1)连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAD+∠ABC=90°,
∵C为弧BE的中点,
∴CE=CB,
∴∠CAE=∠CAB,
∵∠BCD=∠CAE,
∴∠CAB=∠BCD,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB+∠BCD=90°,
∴∠OCD=90°,
∴CD是⊙O的切线;
(2)∵∠BAC=∠CAE,∠ACB=∠ACF=90°,AC=AC,
∴△ABC≌△AFC(ASA),
∴CB=CF,
又∵CB=CE,
∴CE=CF;
(3)∵∠BCD=∠CAD,∠ADC=∠CDB,
∴△DCB∽△DAC,
∴,
∴,
∴AD=2,
∴AB=AD?BD=2?1=1,
设BC=a,AC=a,由勾股定理得:,
解得:,
∴AC=.
23.
解(1)△BDD1为直角三角形
连接DD1,
∵△COD绕点O旋转得到△C1OD1,∴OD1=OD
∵四边形ABCD为菱形,对角线AC、BD相交于点O,
∴OD=OB=BD
∴OD1=OD=OB,
∴∠OD1D=∠ODD1, ∠OBD1 =∠OD1B,
又∵∠OD1D+∠ODD1+∠OBD1 +∠OD1B=180°,
∴∠BD1D=∠OD1D+∠OD1B=90°,
∴△BDD1为直角三角形
(2)①∵四边形ABCD为菱形,对角线AC、BD相交于点O,
∴OD=OB=BD,OA=OC=AC,
∵△COD绕点O旋转得到△C1OD1,
∴OD1=OD,OC=OC1,∠COC1=∠DOD1
∴OD1=OB,OC1 =OA,∠AOC1=∠BOD1
∴=
∴△AOC1∽△BOD1
∴===;
②AC1⊥BD1
∵△AOC1∽△BOD1
∴∠AC1O=∠BD1O
∵四边形ABCD为菱形,对角线AC、BD相交于点O,
∴AC⊥BD,∠COD=90°
∵△COD绕点O旋转得到△C1OD1,
∴∠COD=∠C1OD1=90°
∴∠OD1C1+∠D1C1O=∠OD1C1+∠D1C1A+∠AC1O=90°
∴∠BD1O+∠OD1C1+∠D1C1A =90°
∴∠D1PC1=90°
∴AC1⊥BD1
24.
(1)∵,,
∴,∠ADB=180°-2∠BAD=120°,
∴∠ODB=∠ADB-∠ADO=120°-30°=90°,
∵为的半径,
∴直线是的切线;
(2),,
∴,
∵,
∴,
∴的半径的长为1;
(3)如图,连接,
∵,
∴,OB=2,,
∴,
∵为的直径,∠DME是DE所对的圆周角,
∴,
∴,
∵,
∴,
∵∠DBE=∠MBD,
∴,
∴,
∴.
∴线段的长为.
25.
解:(1)当时,如图,.
∵,
∴,
∴.
(2)结论:.
∵,
∴,
∴
∴.
一、单选题
1.观察下列每组图形,相似图形是( )
A. B.
C. D.
2.下列说法中,正确的是( )
A.两个矩形必相似 B.两个含角的等腰三角形必相似
C.两个菱形必相似 D.两个含角的直角三角形必相似
3.如图,已知,那么添加下列一个条件后,仍然无法判定的是( )
A. B. C. D.
4.如图,是的中位线,,则S四边形DBCE的面积是( )
A.4 B.6 C.2 D.5
5.如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底()7.8米的点处,然后观察者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得米,观察者目高米,则树()的高度约为( )米.
A.15.6 B.6.4 C.3.4 D.3.9
6.如图,在平面直角坐标系中,已知与是位似图形,原点是位似中心,位似比,若,则的长为( ).
A.5 B.6 C.9 D.12
7.如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且,已知DE:DF=3:7,BC=14,则AB的长为( )
A.10.5 B.6 C.7 D.8
8.如图,已知BD与CE相交于点A,DE∥BC,如果AD=2,AB=3,AC=6,那么AE等于( )
A. B. C.4 D.9
9.如图,已知边长为的正方形,是的中点,是的中点,与相交于,和相交于.则四边形的面积为( )
A. B. C. D.
10.如图,在中,点在边上,,,联结,与相交于点,则下列结论一定正确的是( )
A. B. C. D.
11.如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是( )
A.△AOM和△AON都是等边三角形
B.四边形MBON和四边形MODN都是菱形
C.四边形AMON与四边形ABCD是位似图形
D.MO∥BC且BM=CO
12.如图,正方形的对角线,交于点,的平分线交于,交于,且.下列结论中:①;②;③若,则的长为.其中正确的结论有( )
A.①② B.①③ C.②③ D.①②③
二、填空题
13.已知点P是线段AB的一个黄金分割点,且AP>BP,那么AP:AB的比值为______.
14.如图,已知AD,要使ABC∽DEF,还需添加一个条件,你添加的条件是____.(只需写一个条件,不添加辅助线和字母)
15.如图:在中,,,,则________.
16.如图,△ABC是等边三角形,AB=6.点D和E分别在边BC和AC上,且∠ADE=60°,BD=2,则CE的长为_____.
17.如图,在矩形中,对角线,交于点,过点作,交的延长线于点,若,,则的长为________.
18.如图,在中,,在的外部和内部(不包括边)分别取点,,若,,,补角等于,则下列结论:①点在线段的垂直平分线上;②;③;④的最大值是.其中正确的结论是__________.(填写所有正确结论的序号)
三、解答题
19.如图,在中,点、分别在、上,,若,,,求AD的长.
20.如图,在中,点D,E分别在边AB,AC上,连接DE,且.
(1)求证:ADE∽ACB;
(2)若∠B=55°,∠ADE =75°,求∠A的度数.
21.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
①计算小亮在路灯D下的影长;
②计算建筑物AD的高.
22.如图,AB是OO的直径,点D在AB的延长线上,C、E是OO上的两点,C为弧BE的中点,∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是OO的切线:
(2)求证:CE=CF:
(3)若BD=1,CD=,求弦AC的长.
23.如图,已知在菱形ABCD中,对角线AC、BD相交于点O,将△COD绕点O逆时针方向旋转得到△C1OD1,旋转角0°α90°,连结DD1、AC1、BD1,AC1与BD1相交于点P.
(1)判断△BDD1形状,并说明理由;
(2)①求证:;
②判断AC1与BD1的位置关系,并说明理由.
24.如图,为的直径,为延长线上一点,且,,为的弦,连接,连接并延长交于点,连接交于点.
(1)求证:直线是的切线;
(2)求的半径的长;
(3)求线段的长.
25.从三角形(不是等腰三角形)一个顶点引一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在中,,是的完美分割线,且,求的度数.
(2)如图2,在中,,,是的完美分割线,且是以为底边的等腰三角形,找出与的关系.
参考答案
1.C
解:A、两图形形状不同,故不是相似图形;
B、两图形形状不同,故不是相似图形;
C、两图形形状相同,故是相似图形;
D、两图形形状不同,故不是相似图形;
2.D
A、两个矩形的对应角相等,但对应边不一定成比例,则不一定相似,此项错误;
B、如果一个等腰三角形的顶角是,另一等腰三角形的底角是,则不相似,此项错误;
C、两个菱形的对应边成比例,但四个内角不一定对应相等,则不一定相似,此项错误;
D、两个含角的直角三角形必相似,此项正确;
3.B
解:∵∠DAB=∠CAE,
∴∠DAE=∠BAC,
A、若,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项A不符合题意;
B、若,且∠DAE=∠BAC,无法判定△ABC∽△ADE,故选项B符合题意;
C、若∠B=∠D,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项C不符合题意;
D、若∠C=∠AED,且∠DAE=∠BAC,可判定△ABC∽△ADE,故选项D不符合题意;
4.B
解:∵DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,
S△ADE:S△ABC=()2=,
又△ADE的面积是2,
∴△ABC的面积为8,
∴四边形DBCE的面积是8-2=6.
故选:B.
5.D
∵∠AEB=∠CED,∠BAE=∠DCE,
∴RtABE∽RtCDE,
∴,
即,
∴=3.9,
6.C
解:∵△ABC与△DEF是位似图形,
∴AB∥DE,
∴△OAB∽△ODE,
∴,即,
解得:DE=9,
7.A
设AB=x,根据题意得,
8.C
解:∵ED∥BC,
∴ ,
即,
∴AE=4,
9.C
解:∵正方形
∴BC∥AD,AD=BC=AB=2
∵是的中点,
∴
∴△BFH∽△DAH,
∴相似比为
∴△BFH与△DAH相似比为1:2,
∴△BFH与△DAH对应高的比1:2,
∴△BFH的BF边上的高为,△DAH的AD边上的高为,
∴△ADH的面积为,△FBH的面积为;
∵是的中点,
∴
∴
在△ABF和△DAE中
∵
∴△ABF≌△DAE,(SAS)
∴∠BAF=∠ADE,AF=DE
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,
∴∠AIE=90°=∠DAB,
∵∠ADE=∠IDA
∴△AEI∽△EDA,
∴
∵AF=DE=
∴
∴
∴△AEI的面积=
∴四边形BEIH的面积=
10.C
解:∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DE=CF,DF=CE,
∵DE∥BC,DF∥AC,
∴△ADE∽△ABC,△BFD∽△BAC,
∴,故A错误;
,即,故B错误;
∵DF∥AC,∴,故C正确;
∵DE∥BC,∴,故D错误,
11.C
解:∵∠BAD不一定等于为120°,
∴△AOM和△AON不一定都是等边三角形,A错误;
∵BM不一定等于BO,
∴四边形MBON和四边形MODN不一定都是菱形,B错误;
∵四边形ABCD为菱形,
∴AO=OC,又AM=MB,
∴OM∥BC,OM=BC,
同理,ON∥CD,ON=CD,
∴四边形AMON与四边形ABCD是以A为位似中心的位似图形,C正确;
MO∥BC,但BM不一定等于CO,D错误;
故选:C.
12.D
(1)延长DG、BC交于点H,
∵BG平分∠CBD,
∴∠1=∠2,
∵DG⊥BG,
∴∠BGD=∠BGH=90°,
又∵BG=BG,
∴△BGD≌△BGH(ASA),
∴BD=BH,
∴DH=2DG,
∵四边形ABCD是正方形,
∴BC=DC,∠BCF=∠DCH=90°,
又∵∠BGD=90°,∠3=∠4,
∴∠2=∠5,
∴△BCF≌△DCH(ASA),
∴BF=DH,
∴BF=2DG;①正确;
∵四边形ABCD是正方形,
∴∠ACB=∠BDC=45°,
∴∠BCE=∠BDF,
又∵∠1=∠2,
∴△BEC∽△BFD,②正确
∵BC=CD,BC2+CD2=BD2,
∴BD=BC
∴,
∵,
∴BF=.③正确
故选D.
13.
∵点P是线段的一个黄金分割点,且,
∴AP:AB=.
14.AB∥DE
∵∠A=∠D,
∴当∠B=∠DEF时,△ABC∽△DEF,
∵AB∥DE时,∠B=∠DEF,
∴添加AB∥DE时,使△ABC∽△DEF.
故答案为:AB∥DE.
15.9
∵,
∴△ADE∽△ABC,
∴相似比=,
∵,,
∴AB=AD+BD=3,
∴,
∴,
故答案为:9.
16..
∵△ABC是等边三角形,
∴∠B=∠C=60?,AB=BC=6,
∴∠BAD+∠ADB=180?-∠B=180?-60?=120?,
∵∠ADE=60°,
∴∠ADB+∠EDC=180?-∠ADE=180?-60?=120?,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴,
∵BD=2,
∴CD=BC-BD=6-2=4,
∴,
∴,
故答案为:.
17.
如图所示,作DF⊥AC于F点,
在Rt△ABC中,,,
根据矩形的性质可得:∠BAC=∠FCD,,
∴△ABC∽△CFD,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
故答案为:.
18.①②
∵AD=AE=4,
∴点A在线段DE的垂直平分线上;故①正确;
如图,延长DA至F,则∠CAF+∠CAD=180°,
∵∠BAC=120°,
∴∠ACB+∠ABC=60°,∠BAD+∠CAF=60°,
∵补角等于,
∴∠CAE=∠CAF,
∴∠ACB+∠ABC=∠BAD+∠CAE,故②正确,
∵,,,
∴=2,
∵不能证明∠ADB=∠CEA,
∴不能判定△ACE∽△BAD,故③错误,
∵2<AC<6,4<AB<12,
∴6<BC<18,
∴不能确定BC的最大值;故④错误;
综上所述:正确的结论为①②,
19.AD=4
解:∵DE∥BC,
∴,
设AD=x,则,
∴,
解得:x=4或﹣4(舍去),
即AD=4.
20.
(1)证明:∵,
∴.
又∵∠A=∠A,
∴△ADE∽△ACB;
(2)解:∵△ADE∽△ACB,
∴∠ADE=∠ACB,
∵∠ADE=75°,∴∠ACB=75°.
又∵∠B=55°,
∴∠A=180°-∠ACB-∠B=50°.
21.①1.5米 ②12米
①∵
∴ ,
,
∴ ,
∴AB=10,
∴BQ = 10- 2- 6.5= 1.5,
即小亮在路灯D下的影长是1.5米.
②∵
∴,
∴ ,
,
∴ ,
解得DA=12,
∴建筑物的高为12米.
22.
(1)连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAD+∠ABC=90°,
∵C为弧BE的中点,
∴CE=CB,
∴∠CAE=∠CAB,
∵∠BCD=∠CAE,
∴∠CAB=∠BCD,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB+∠BCD=90°,
∴∠OCD=90°,
∴CD是⊙O的切线;
(2)∵∠BAC=∠CAE,∠ACB=∠ACF=90°,AC=AC,
∴△ABC≌△AFC(ASA),
∴CB=CF,
又∵CB=CE,
∴CE=CF;
(3)∵∠BCD=∠CAD,∠ADC=∠CDB,
∴△DCB∽△DAC,
∴,
∴,
∴AD=2,
∴AB=AD?BD=2?1=1,
设BC=a,AC=a,由勾股定理得:,
解得:,
∴AC=.
23.
解(1)△BDD1为直角三角形
连接DD1,
∵△COD绕点O旋转得到△C1OD1,∴OD1=OD
∵四边形ABCD为菱形,对角线AC、BD相交于点O,
∴OD=OB=BD
∴OD1=OD=OB,
∴∠OD1D=∠ODD1, ∠OBD1 =∠OD1B,
又∵∠OD1D+∠ODD1+∠OBD1 +∠OD1B=180°,
∴∠BD1D=∠OD1D+∠OD1B=90°,
∴△BDD1为直角三角形
(2)①∵四边形ABCD为菱形,对角线AC、BD相交于点O,
∴OD=OB=BD,OA=OC=AC,
∵△COD绕点O旋转得到△C1OD1,
∴OD1=OD,OC=OC1,∠COC1=∠DOD1
∴OD1=OB,OC1 =OA,∠AOC1=∠BOD1
∴=
∴△AOC1∽△BOD1
∴===;
②AC1⊥BD1
∵△AOC1∽△BOD1
∴∠AC1O=∠BD1O
∵四边形ABCD为菱形,对角线AC、BD相交于点O,
∴AC⊥BD,∠COD=90°
∵△COD绕点O旋转得到△C1OD1,
∴∠COD=∠C1OD1=90°
∴∠OD1C1+∠D1C1O=∠OD1C1+∠D1C1A+∠AC1O=90°
∴∠BD1O+∠OD1C1+∠D1C1A =90°
∴∠D1PC1=90°
∴AC1⊥BD1
24.
(1)∵,,
∴,∠ADB=180°-2∠BAD=120°,
∴∠ODB=∠ADB-∠ADO=120°-30°=90°,
∵为的半径,
∴直线是的切线;
(2),,
∴,
∵,
∴,
∴的半径的长为1;
(3)如图,连接,
∵,
∴,OB=2,,
∴,
∵为的直径,∠DME是DE所对的圆周角,
∴,
∴,
∵,
∴,
∵∠DBE=∠MBD,
∴,
∴,
∴.
∴线段的长为.
25.
解:(1)当时,如图,.
∵,
∴,
∴.
(2)结论:.
∵,
∴,
∴
∴.
