湘教版八年级数学下册期中达标检测卷(含答案)
文档属性
| 名称 | 湘教版八年级数学下册期中达标检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 08:22:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版八年级数学下册
期中达标检测卷
(本试卷分第Ⅰ卷和第Ⅱ卷,考试时间:120分钟,赋分:120分)
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.在一个直角三角形中,有一个锐角等于55°,则另一个锐角的度数是
( )
A.115°
B.125°
C.25°
D.35°
2.下列四组数据中不能作为直角三角形的三边长的是( )
A.3,4,6
B.5,12,13
C.8,15,17
D.,,2
3.矩形、菱形、正方形都一定具有的性质是
( )
A.邻边相等
B.四个角都是直角
C.对角线相等
D.对角线互相平分
4.在△ABC中,∠C=90°,AD为角平分线,BC=32
cm,BD∶DC=9∶7,则点D到AB的距离为
( )
A.18
cm
B.16
cm
C.14
cm
D.12
cm
5.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS
B.ASA
C.SAS
D.HL
6.下列图形中属于中心对称图形的是( )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
7.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,EF∥BC交AC于点M,若CM=5,则CE2+CF2=( )
A.75
B.100
C.120
D.125
eq
\o(\s\up7(),\s\do5(第7题图))
eq
\o(\s\up7(),\s\do5(第8题图))
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
A.
B.
C.12
D.24
9.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为
( )
A.4
s
B.3
s
C.2
s
D.1
s
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10
B.12
C.18
D.24
将一个边长为10的正方形铁片(如图),过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线的长度所标的数据不可能的是
( )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.★如图,四边形ABCD是正方形,直线a,b,c分别通过A,D,C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是
( )
A.36
B.45
C.54
D.64
第Ⅱ卷 (非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.一个多边形的内角和是1
800°,则这个多边形的边数为
.
14.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是
.
eq
\o(\s\up7(),\s\do5(第14题图))
eq
\o(\s\up7(),\s\do5(第15题图))
15.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC=
.
16.如图,∠AOB=60°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DOC=
.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.★如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得塔尖D的仰角∠DAC=15°,向塔正前方水平直行260
m到达点B,测得塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6
m,塔的高度DE=
m.
18.矩形纸片ABCD中,AD=10
cm,AB=4
cm,按如图方式折叠,使点D与点B重合,折痕为EF,则DE=
cm.
三、解答题(本大题共8小题,满分66分,解答在写出文字说明、证明过程或演算步骤)
19.(本题满分10分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
20.(本题满分5分)如图,四边形ABCD和BCEF均为平行四边形,AD=2
cm,∠A=65°,∠E=33°,求EF的长和∠BGC的度数.
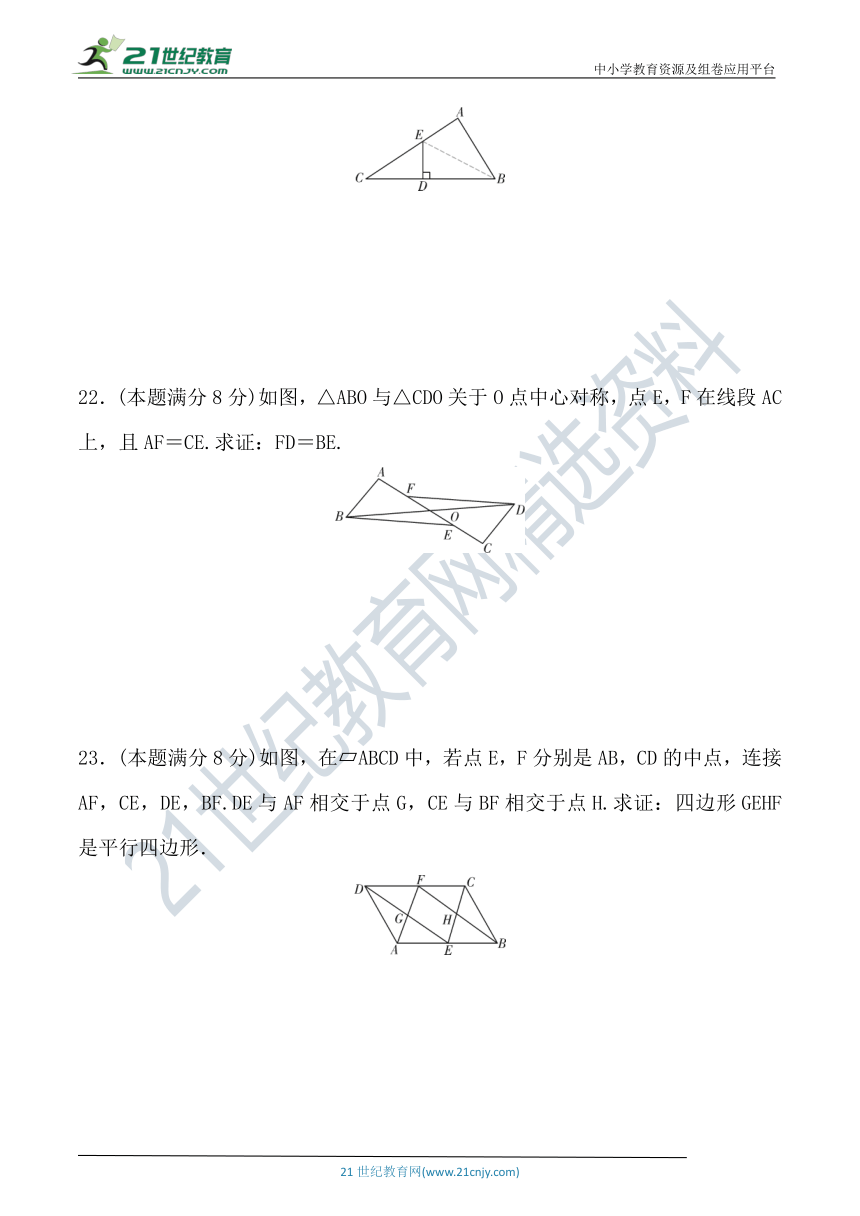
21.(本题满分6分)如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的平分线上.
22.(本题满分8分)如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.
23.(本题满分8分)如图,在?ABCD中,若点E,F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形.
24.(本题满分8分)一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”
于是大家讨论开了,小亮说:“拼成的是平行四边形”;小华说:“拼成的是矩形”;小强说:“拼成的是菱形”;小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由.
25.(本题满分11分)如图,在?ABCD中,AE⊥BC于点E,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
26.(本题满分10分)已知:正方形ABCD的两条对角线相交于点O,E是线段OC上的一动点,过点A作AG⊥BE于点G,交BD于点F.
(1)若动点E在线段OC上(不含端点),如图①,求证:OF=OE;
(2)若动点E在线段OC的延长线上,如图②,试判断△OEF的形状,并说明理由.
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
参考答案
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.在一个直角三角形中,有一个锐角等于55°,则另一个锐角的度数是
( D )
A.115°
B.125°
C.25°
D.35°
2.下列四组数据中不能作为直角三角形的三边长的是( A )
A.3,4,6
B.5,12,13
C.8,15,17
D.,,2
3.矩形、菱形、正方形都一定具有的性质是
( D )
A.邻边相等
B.四个角都是直角
C.对角线相等
D.对角线互相平分
4.在△ABC中,∠C=90°,AD为角平分线,BC=32
cm,BD∶DC=9∶7,则点D到AB的距离为
( C )
A.18
cm
B.16
cm
C.14
cm
D.12
cm
5.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( D )
A.SSS
B.ASA
C.SAS
D.HL
6.下列图形中属于中心对称图形的是( C )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
7.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,EF∥BC交AC于点M,若CM=5,则CE2+CF2=( B )
A.75
B.100
C.120
D.125
eq
\o(\s\up7(),\s\do5(第7题图))
eq
\o(\s\up7(),\s\do5(第8题图))
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( A )
A.
B.
C.12
D.24
9.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为
( B )
A.4
s
B.3
s
C.2
s
D.1
s
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( B )
A.10
B.12
C.18
D.24
将一个边长为10的正方形铁片(如图),过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线的长度所标的数据不可能的是
( B )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.★如图,四边形ABCD是正方形,直线a,b,c分别通过A,D,C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是
( B )
A.36
B.45
C.54
D.64
第Ⅱ卷 (非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.一个多边形的内角和是1
800°,则这个多边形的边数为__12__.
14.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是__∠A=90°或AD=BC或AB∥CD(写出一种情况即可)__.
eq
\o(\s\up7(),\s\do5(第14题图))
eq
\o(\s\up7(),\s\do5(第15题图))
15.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC=__40°__.
16.如图,∠AOB=60°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DOC=__30°__.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.★如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得塔尖D的仰角∠DAC=15°,向塔正前方水平直行260
m到达点B,测得塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6
m,塔的高度DE=__131.6__m.
18.矩形纸片ABCD中,AD=10
cm,AB=4
cm,按如图方式折叠,使点D与点B重合,折痕为EF,则DE=__5.8__cm.
三、解答题(本大题共8小题,满分66分,解答在写出文字说明、证明过程或演算步骤)
19.(本题满分10分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
解:设这个多边形的边数是n,则
(n-2)×180°=360°×4,
n-2=8,
n=10.
答:这个多边形的边数是10.
20.(本题满分5分)如图,四边形ABCD和BCEF均为平行四边形,AD=2
cm,∠A=65°,∠E=33°,求EF的长和∠BGC的度数.
解:∵四边形ABCD为平行四边形,
AD=2
cm,∠A=65°,
∴BC=AD=2
cm,∠BCD=∠A=65°
∵四边形BCEF为平行四边形,∠E=33°,
∴EF=BC=2
cm,∠CBG=∠E=33°,
∴∠BGC=180°-65°-33°=82°.
21.(本题满分6分)如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的平分线上.
证明:连接BE,
∵ED⊥BC,
∴∠BDE=∠A=90°.
在Rt△ABE和Rt△DBE中,
∴Rt△ABE≌Rt△DBE(HL).
∴∠ABE=∠DBE.
∴点E在∠ABC的平分线上.
22.(本题满分8分)如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.
证明:∵△ABO与△CDO关于O点中心对称,
∴OB=OD,
OA=OC.
又∵AF=CE,∴OF=OE.
∵在△DOF和△BOE中,
∴△DOF≌△BOE(SAS).
∴FD=BE.
23.(本题满分8分)如图,在?ABCD中,若点E,F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB中点,F是CD中点,
∴AE=CF,AE∥CF,
∴四边形AECF是平行四边形,∴AF∥CE.
同理可证DE∥BF,
∴四边形GEHF是平行四边形.
24.(本题满分8分)一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”
于是大家讨论开了,小亮说:“拼成的是平行四边形”;小华说:“拼成的是矩形”;小强说:“拼成的是菱形”;小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由.
解:都不赞同,因为△ABC形状不确定,所以应分情况讨论:
(1)若△ABC中,AB≠AC且∠BAC≠90°时,如图①,△ABC与它的中心对称图形拼成了一个平行四边形.
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
eq
\o(\s\up7(),\s\do5(③))
eq
\o(\s\up7(),\s\do5(④))
理由:∵点B与点C、点A与点D关于点O对称,
∴OA=OD,OB=OC,
∴四边形ABDC是平行四边形.
(2)若△ABC中,AB=AC且∠BAC≠90°时,如图②,△ABC与它的中心对称图形拼成了一个菱形.理由:由题意可得,AC=BD,AB=CD,
又∵AB=AC,∴AB=BD=DC=AC,∴四边形ABDC是菱形.
(3)若△ABC中,AB≠AC且∠BAC=90°时,如图③,△ABC与它的中心对称图形拼成了一个矩形,理由:由(1)得四边形ABDC是平行四边形,
∵∠BAC=90°,∴四边形ABDC是矩形.
(4)若△ABC中,AB=AC且∠BAC=90°时,如图④,
△ABC与它的中心对称图形拼成了一个正方形.
理由:由(3)得四边形ABDC是矩形,
∵AB=BC,∴四边形ABDC是正方形.
综上所述,都不赞同.
25.(本题满分11分)如图,在?ABCD中,AE⊥BC于点E,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即EF=BC.
∵?ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,∴∠AEF=90°.
∴四边形AEFD是矩形.
(2)解:∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.∵AE⊥BF,
∴△ABF的面积=AB·AF=BF·AE.
∴AE===.
26.(本题满分10分)已知:正方形ABCD的两条对角线相交于点O,E是线段OC上的一动点,过点A作AG⊥BE于点G,交BD于点F.
(1)若动点E在线段OC上(不含端点),如图①,求证:OF=OE;
(2)若动点E在线段OC的延长线上,如图②,试判断△OEF的形状,并说明理由.
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
(1)证明:∵四边形ABCD为正方形,
∴OA=OB,∠AOB=∠BOC=90°.
∵AG⊥BE于点G,∴∠AGE=90°,
∴∠GAE+∠AEG=∠OBE+∠BEO=90°,
∴∠GAE=∠OBE.
在△AOF和△BOE中,
∴△AOF≌△BOE(ASA),
∴OF=OE.
(2)解:△OEF是等腰直角三角形,
理由:如图②,连接EF,
与(1)同理,可证明△AOF≌△BOE(ASA),
∴OF=OE.又∠BOC=90°,
∴△OEF是等腰直角三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
湘教版八年级数学下册
期中达标检测卷
(本试卷分第Ⅰ卷和第Ⅱ卷,考试时间:120分钟,赋分:120分)
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.在一个直角三角形中,有一个锐角等于55°,则另一个锐角的度数是
( )
A.115°
B.125°
C.25°
D.35°
2.下列四组数据中不能作为直角三角形的三边长的是( )
A.3,4,6
B.5,12,13
C.8,15,17
D.,,2
3.矩形、菱形、正方形都一定具有的性质是
( )
A.邻边相等
B.四个角都是直角
C.对角线相等
D.对角线互相平分
4.在△ABC中,∠C=90°,AD为角平分线,BC=32
cm,BD∶DC=9∶7,则点D到AB的距离为
( )
A.18
cm
B.16
cm
C.14
cm
D.12
cm
5.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS
B.ASA
C.SAS
D.HL
6.下列图形中属于中心对称图形的是( )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
7.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,EF∥BC交AC于点M,若CM=5,则CE2+CF2=( )
A.75
B.100
C.120
D.125
eq
\o(\s\up7(),\s\do5(第7题图))
eq
\o(\s\up7(),\s\do5(第8题图))
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
A.
B.
C.12
D.24
9.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为
( )
A.4
s
B.3
s
C.2
s
D.1
s
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10
B.12
C.18
D.24
将一个边长为10的正方形铁片(如图),过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线的长度所标的数据不可能的是
( )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.★如图,四边形ABCD是正方形,直线a,b,c分别通过A,D,C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是
( )
A.36
B.45
C.54
D.64
第Ⅱ卷 (非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.一个多边形的内角和是1
800°,则这个多边形的边数为
.
14.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是
.
eq
\o(\s\up7(),\s\do5(第14题图))
eq
\o(\s\up7(),\s\do5(第15题图))
15.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC=
.
16.如图,∠AOB=60°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DOC=
.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.★如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得塔尖D的仰角∠DAC=15°,向塔正前方水平直行260
m到达点B,测得塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6
m,塔的高度DE=
m.
18.矩形纸片ABCD中,AD=10
cm,AB=4
cm,按如图方式折叠,使点D与点B重合,折痕为EF,则DE=
cm.
三、解答题(本大题共8小题,满分66分,解答在写出文字说明、证明过程或演算步骤)
19.(本题满分10分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
20.(本题满分5分)如图,四边形ABCD和BCEF均为平行四边形,AD=2
cm,∠A=65°,∠E=33°,求EF的长和∠BGC的度数.
21.(本题满分6分)如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的平分线上.
22.(本题满分8分)如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.
23.(本题满分8分)如图,在?ABCD中,若点E,F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形.
24.(本题满分8分)一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”
于是大家讨论开了,小亮说:“拼成的是平行四边形”;小华说:“拼成的是矩形”;小强说:“拼成的是菱形”;小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由.
25.(本题满分11分)如图,在?ABCD中,AE⊥BC于点E,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
26.(本题满分10分)已知:正方形ABCD的两条对角线相交于点O,E是线段OC上的一动点,过点A作AG⊥BE于点G,交BD于点F.
(1)若动点E在线段OC上(不含端点),如图①,求证:OF=OE;
(2)若动点E在线段OC的延长线上,如图②,试判断△OEF的形状,并说明理由.
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
参考答案
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1.在一个直角三角形中,有一个锐角等于55°,则另一个锐角的度数是
( D )
A.115°
B.125°
C.25°
D.35°
2.下列四组数据中不能作为直角三角形的三边长的是( A )
A.3,4,6
B.5,12,13
C.8,15,17
D.,,2
3.矩形、菱形、正方形都一定具有的性质是
( D )
A.邻边相等
B.四个角都是直角
C.对角线相等
D.对角线互相平分
4.在△ABC中,∠C=90°,AD为角平分线,BC=32
cm,BD∶DC=9∶7,则点D到AB的距离为
( C )
A.18
cm
B.16
cm
C.14
cm
D.12
cm
5.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( D )
A.SSS
B.ASA
C.SAS
D.HL
6.下列图形中属于中心对称图形的是( C )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
7.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,EF∥BC交AC于点M,若CM=5,则CE2+CF2=( B )
A.75
B.100
C.120
D.125
eq
\o(\s\up7(),\s\do5(第7题图))
eq
\o(\s\up7(),\s\do5(第8题图))
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( A )
A.
B.
C.12
D.24
9.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为
( B )
A.4
s
B.3
s
C.2
s
D.1
s
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( B )
A.10
B.12
C.18
D.24
将一个边长为10的正方形铁片(如图),过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线的长度所标的数据不可能的是
( B )
eq
\o(\s\up7(),\s\do5(A))
eq
\o(\s\up7(),\s\do5(B))
eq
\o(\s\up7(),\s\do5(C))
eq
\o(\s\up7(),\s\do5(D))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.★如图,四边形ABCD是正方形,直线a,b,c分别通过A,D,C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是
( B )
A.36
B.45
C.54
D.64
第Ⅱ卷 (非选择题 共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13.一个多边形的内角和是1
800°,则这个多边形的边数为__12__.
14.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是__∠A=90°或AD=BC或AB∥CD(写出一种情况即可)__.
eq
\o(\s\up7(),\s\do5(第14题图))
eq
\o(\s\up7(),\s\do5(第15题图))
15.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC=__40°__.
16.如图,∠AOB=60°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DOC=__30°__.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.★如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得塔尖D的仰角∠DAC=15°,向塔正前方水平直行260
m到达点B,测得塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6
m,塔的高度DE=__131.6__m.
18.矩形纸片ABCD中,AD=10
cm,AB=4
cm,按如图方式折叠,使点D与点B重合,折痕为EF,则DE=__5.8__cm.
三、解答题(本大题共8小题,满分66分,解答在写出文字说明、证明过程或演算步骤)
19.(本题满分10分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
解:设这个多边形的边数是n,则
(n-2)×180°=360°×4,
n-2=8,
n=10.
答:这个多边形的边数是10.
20.(本题满分5分)如图,四边形ABCD和BCEF均为平行四边形,AD=2
cm,∠A=65°,∠E=33°,求EF的长和∠BGC的度数.
解:∵四边形ABCD为平行四边形,
AD=2
cm,∠A=65°,
∴BC=AD=2
cm,∠BCD=∠A=65°
∵四边形BCEF为平行四边形,∠E=33°,
∴EF=BC=2
cm,∠CBG=∠E=33°,
∴∠BGC=180°-65°-33°=82°.
21.(本题满分6分)如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的平分线上.
证明:连接BE,
∵ED⊥BC,
∴∠BDE=∠A=90°.
在Rt△ABE和Rt△DBE中,
∴Rt△ABE≌Rt△DBE(HL).
∴∠ABE=∠DBE.
∴点E在∠ABC的平分线上.
22.(本题满分8分)如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.
证明:∵△ABO与△CDO关于O点中心对称,
∴OB=OD,
OA=OC.
又∵AF=CE,∴OF=OE.
∵在△DOF和△BOE中,
∴△DOF≌△BOE(SAS).
∴FD=BE.
23.(本题满分8分)如图,在?ABCD中,若点E,F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB中点,F是CD中点,
∴AE=CF,AE∥CF,
∴四边形AECF是平行四边形,∴AF∥CE.
同理可证DE∥BF,
∴四边形GEHF是平行四边形.
24.(本题满分8分)一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”
于是大家讨论开了,小亮说:“拼成的是平行四边形”;小华说:“拼成的是矩形”;小强说:“拼成的是菱形”;小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由.
解:都不赞同,因为△ABC形状不确定,所以应分情况讨论:
(1)若△ABC中,AB≠AC且∠BAC≠90°时,如图①,△ABC与它的中心对称图形拼成了一个平行四边形.
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
eq
\o(\s\up7(),\s\do5(③))
eq
\o(\s\up7(),\s\do5(④))
理由:∵点B与点C、点A与点D关于点O对称,
∴OA=OD,OB=OC,
∴四边形ABDC是平行四边形.
(2)若△ABC中,AB=AC且∠BAC≠90°时,如图②,△ABC与它的中心对称图形拼成了一个菱形.理由:由题意可得,AC=BD,AB=CD,
又∵AB=AC,∴AB=BD=DC=AC,∴四边形ABDC是菱形.
(3)若△ABC中,AB≠AC且∠BAC=90°时,如图③,△ABC与它的中心对称图形拼成了一个矩形,理由:由(1)得四边形ABDC是平行四边形,
∵∠BAC=90°,∴四边形ABDC是矩形.
(4)若△ABC中,AB=AC且∠BAC=90°时,如图④,
△ABC与它的中心对称图形拼成了一个正方形.
理由:由(3)得四边形ABDC是矩形,
∵AB=BC,∴四边形ABDC是正方形.
综上所述,都不赞同.
25.(本题满分11分)如图,在?ABCD中,AE⊥BC于点E,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即EF=BC.
∵?ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,∴∠AEF=90°.
∴四边形AEFD是矩形.
(2)解:∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.∵AE⊥BF,
∴△ABF的面积=AB·AF=BF·AE.
∴AE===.
26.(本题满分10分)已知:正方形ABCD的两条对角线相交于点O,E是线段OC上的一动点,过点A作AG⊥BE于点G,交BD于点F.
(1)若动点E在线段OC上(不含端点),如图①,求证:OF=OE;
(2)若动点E在线段OC的延长线上,如图②,试判断△OEF的形状,并说明理由.
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
(1)证明:∵四边形ABCD为正方形,
∴OA=OB,∠AOB=∠BOC=90°.
∵AG⊥BE于点G,∴∠AGE=90°,
∴∠GAE+∠AEG=∠OBE+∠BEO=90°,
∴∠GAE=∠OBE.
在△AOF和△BOE中,
∴△AOF≌△BOE(ASA),
∴OF=OE.
(2)解:△OEF是等腰直角三角形,
理由:如图②,连接EF,
与(1)同理,可证明△AOF≌△BOE(ASA),
∴OF=OE.又∠BOC=90°,
∴△OEF是等腰直角三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
