沪教版(上海)八年级数学寒假班讲义——07无理方程(学生版+教师版)
文档属性
| 名称 | 沪教版(上海)八年级数学寒假班讲义——07无理方程(学生版+教师版) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 21:45:58 | ||
图片预览




文档简介
1047750010617200初二数学寒假班(教师版)
教师
日期
学生
课程编号
课型
同步/专题
课题
无理方程及应用
教学目标
理解无理方程的概念;掌握简单的无理方程的解法,知道“验根”是解无理方程的必要步骤,掌握验根的基本方法.
熟练的解决无理方程的应用问题.
教学重点
1.无理方程的解法;
2.无理方程有可能产生增根的理解.
教学安排
版块
时长
1
无理方程的概念及解法
50分钟
2
无理方程的应用
30分钟
3
课堂练习
40分钟
1111250146050无理方程
无理方程
-37147516510 知识结构
知识结构
386080147955模块一:无理方程的概念和解法
模块一:无理方程的概念和解法
-2171705080知识精讲
知识精讲
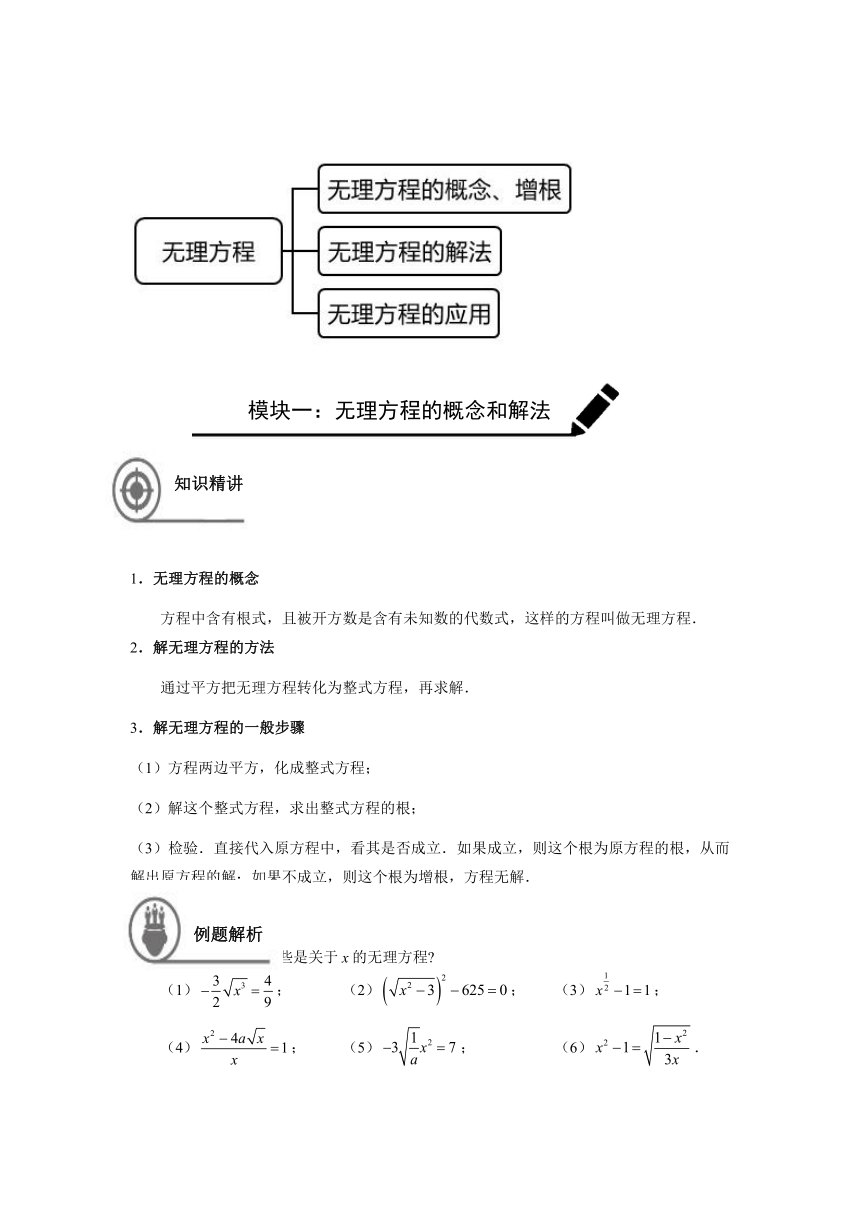
1.无理方程的概念
方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程.
2.解无理方程的方法
通过平方把无理方程转化为整式方程,再求解.
3.解无理方程的一般步骤
(1)方程两边平方,化成整式方程;
(2)解这个整式方程,求出整式方程的根;
(3)检验.直接代入原方程中,看其是否成立.如果成立,则这个根为原方程的根,从而解出原方程的解;如果不成立,则这个根为增根,方程无解.
-60325-154940例题解析
例题解析
下列方程是哪些是关于false的无理方程?
(1)false; (2)false; (3)false;
(4)false; (5)false; (6)false.
下列哪个方程有实数解( )
A.false B.false
C.false D.false
若方程false有解,则false的取值范围是________.
不解方程,说明下列方程是否有实数根:
(1)false;
(2)false.
用换元法解方程false时,设false.则该方程转换整式方程是____________.
解下列方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false;
解下列方程:
(1)false; (2)false.
解方程:false.
解方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false.
解下列方程:false.
解下列方程:false.
72199549530模块二:无理方程的根的讨论
模块二:无理方程的根的讨论
-201930147320知识精讲
知识精讲
3.增根的概念
-114300495300例题解析
例题解析
无理方程在化整式方程求解过程中,整式方程的解如果使得无理方程左右两边不相等,那么这个解就是方程的增根.
关于false的方程false有一个增根x=4,求:
a的值;
方程的根.
若方程false有一个根是false,求实数m的值.
若关于x的无理方程false有实数根,求k的取值范围.
若关于x的方程false只有一个实数根,求m的取值范围.
72199549530模块三:无理方程的应用
模块三:无理方程的应用
-201930233680知识精讲
知识精讲
4.应用
-68580233045例题解析
例题解析
寻找题目中的等量关系,列方程,求解,根据实际情况进行取舍.
用一根56厘米的细铁丝弯折成一个直角三角形,使它的一条直角边长为7厘米, 求这个直角三角形的另两条边的长度.
建一块场地,用600块正方形的砖头铺成,如果把场地的面积扩大到原来面积的2 倍还多0.6平方米,且正方形的砖头的边长增加10厘米,则需要铺540块方砖,求原 场地的面积.
若Q点在直线false上,且Q到点P(0,2)的距离为false,求Q点的坐标.
37306251118235A
B
P
N
M
O
l1
l2
A
B
P
N
M
O
l1
l2
false与false为两条互相垂直的大路,小李和老王从十字路口O点同时出发,分别沿着 图示的方向以1千米/小时和2千米/小时的速度前进,到达A与B地,一座学校座落于 距false8千米,距false5千米的P处,问:经过多少时间,两人距离学校的路程刚好相等? 是几千米?
有一群蜜蜂,一部分飞进了枸杞里,其个数等于总数的一半的平方根,还有全体
的false遗留在后面,此外,这群里还有一个小蜜蜂在莲花旁徘徊着,它被一个坠入香花陷
阱的同伴的呻吟声所吸引.试问:这群蜜蜂共有多少个?
m、n为两段互相垂直的笔直的公路,工厂A在公路n上,距离公路m为1千米.工 厂B距离公路m为2千米,且距离公路n为3千米,现在要在公路m上选一个地址造 一个车站P,使它与A、B两厂的距离和为false千米,试指出车站P的位置?
如图,x轴表示一条东西方向的道路,y表示一条南北方向的道路,小丽和小明分 别从十字路口O点处同时出发,小丽沿着x轴以4千米/时的速度由西向东前进,小明 沿着y轴以5千米/时的速度由南向北前进,有一棵百年古树位于图中的P点处,古树 与x轴、y轴的距离分别是3千米和2千米,问:
离开路口后,经过多长时间,两人与古树的距离恰好相等?
离开路口后多少时间,两人与这课古树所处的位置恰好在一条直线上?
随堂检测
随堂检测
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
根据平方根的意义,直接判断下列方程是否有解,并简述理由:
(1)false; (2)false;
(3)false; (4)false.
方程false的实数解为( ).
A.false B.false C.false D.false
用换元法解方程false时,设false.则该方程 可转换成整式方程是_________.
解方程:
(1)false; (2)false.
解方程:
(1)false; (2)false.
解方程:
(1)false;
(2)false.
有两块正方形木板,其中大的一块木板面积比小的木板面积大45平方米,小的木板的边长比大的木板的边长短3分米,求这块小木板的面积.
如果false轴上一点P到两点A(3,5)、B(-1,-2)的距离相等,求P点的坐标.
解方程:false.
解方程:false.
已知a为非负整数,若关于x的方程false至少有一个整数根,
求a的值.
4686300562610A地在M地的正北方向12千米处,B地在M地的正东方向12千米处,某人从 B地出发向正西方向行至C地,再沿CA方向到达A地,这样比由B地到M地再到A 地的路程少4千米,求M地与C地之间的距离.
-1143005080课后作业
课后作业
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
下列无理方程有解的方程是( ).
A.false B.false
C.false D.false
下列四个无理方程中,有一个根是x=2的方程是( ).
A.false B.false
C.false D.false
用换元法解false方程时,设false=y,则原方程可转换成整式方程_____________.
将下列方程化成有理方程:
(1)false; (2)false; (3)false.
解下列方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false.
有一个数,它的平方根比它的倒数的正平方根的3倍多2,求这个数.
已知点P是x轴上一点,它与点A(-9,3)之间的距离是15,求点P的坐标.
某学校修建两块面积相等的绿地,一块是长方形,另一块是正方形.已知长方形绿地的长比宽多14米,且这两块绿地的周长之和为196米,那么长方形绿地的宽是多少?
解下列方程:
(1)false; (2)false.
解下列关于false的方程:
(1)false; (2)false.
若关于x的方程false有实数根,求k的取值范围.
1047750010617200初二数学寒假班(教师版)
教师
日期
学生
课程编号
课型
同步/专题
课题
无理方程及应用
教学目标
理解无理方程的概念;掌握简单的无理方程的解法,知道“验根”是解无理方程的必要步骤,掌握验根的基本方法.
熟练的解决无理方程的应用问题.
教学重点
1.无理方程的解法;
2.无理方程有可能产生增根的理解.
教学安排
版块
时长
1
无理方程的概念及解法
50分钟
2
无理方程的应用
30分钟
3
课堂练习
40分钟
1111250146050无理方程
无理方程
-37147516510 知识结构
知识结构
386080147955模块一:无理方程的概念和解法
模块一:无理方程的概念和解法
-2171705080知识精讲
知识精讲
1.无理方程的概念
方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程.
2.解无理方程的方法
通过平方把无理方程转化为整式方程,再求解.
3.解无理方程的一般步骤
(1)方程两边平方,化成整式方程;
(2)解这个整式方程,求出整式方程的根;
(3)检验.直接代入原方程中,看其是否成立.如果成立,则这个根为原方程的根,从而解出原方程的解;如果不成立,则这个根为增根,方程无解.
-60325-154940例题解析
例题解析
下列方程是哪些是关于false的无理方程?
(1)false; (2)false; (3)false;
(4)false; (5)false; (6)false.
【难度】★
【答案】(1)、(2)、(3)、(4)、(6)是无理方程.
【解析】根据无理方程的概念,方程中含有根式,并且被开方数是含有未知数的代数式的方
程叫做无理方程,可知(1)、(2)、(4)、(6)都是无理方程,false,可知(3)也
是无理方程.
【总结】考查无理方程的概念,方程中根号内含有未知数即可.
下列哪个方程有实数解( )
A.false B.false
C.false D.false
【难度】★
【答案】D
【解析】根据二次根式的双重非负性,对A选项,false,此时false,故方程
无实数解;对B选项,false,可知方程无实数解;对C选项,false,
false无解,即方程无实数解;故选D.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行简单判定.
若方程false有解,则false的取值范围是________.
【难度】★
【答案】false.
【解析】移项得false,方程有解,根据二次根式的非负性,可得false,得false.
【总结】考查无理方程有解的应用,根据二次根式的非负性即可进行判断.
不解方程,说明下列方程是否有实数根:
(1)false;
(2)false.
【难度】★
【答案】(1)有唯一实数根false;
(2)当false时,方程无实数根;当false时,方程有无数个实数根.
【解析】(1)根据二次根式的非负性,可得:false,即得false的定义域为false,
此时false,即得方程有唯一实数根false;
当false时,则有false,根据二次根式非负性,可知方程无实数根;
当false时,等式恒成立,可知方程有无数实数根,满足false即可.
【总结】考查对无理方程解的判断,对部分方程根据二次根式双重非负性即可进行判定.
用换元法解方程false时,设false.则该方程转换整式方程是____________.
【难度】★
【答案】false.
【解析】由false,可得false,原方程即为false,
整理即为false.
【总结】考查用“换元法”对无理方程进行变形转化,注意最终要化成整式形式.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方,得:false,整理得:false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false;
移项得:false,两边平方得:false,
因式分解整理得:false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解下列方程:
(1)false; (2)false;
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方,得:false,整理得:false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false;
(2)由原式得:false或false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意无理方程的验根.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方得:false,整理得:false,
配方法解得:false,false,
经检验,false是原方程的增根,即原方程的根为false;
(2)移项得false,两边平方得false,整理得false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解方程:false.
【难度】★★
【答案】false,false.
【解析】令false,则false,原方程即为false,解得:false,false,
则有false或false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查利用“换元法”解无理方程,注意观察无理方程含未知数的根式之间的联系.
解方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false,false;(2)false,false.
【解析】(1)令false,得false,原方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根;
(2)令false,得false,原方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查用“换元法”解无理方程,注意根据元的取值范围舍去增根.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)移项得false,两边平方得false,
移项得false,两边平方得false,解得:false,
经检验,false是原方程的根;
(2)两边平方得false,移项得false,
两边平方整理得false,配方法解得:false,false,
经检验,false是原方程的增根,即原方程的根是false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
解下列方程:false.
【难度】★★★
【答案】false.
【解析】平方得false,移项得false,
两边平方整理得false,解得:false,false,
经检验,false是原方程的增根,即原方程的根是false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
解下列方程:false.
【难度】★★★
【答案】false.
【解析】令false,则有false,由此原方程可变形得:
false,整理即为false,
因式分解法解得:false,false,即false或false,
由false,整理得false,解得:false,false,
经检验,false是原方程的增根,
由false,可解得:false,经检验,false是原方程的增根,
综上所述,原方程的根是false.
【总结】考查较复杂的换元法的转化解无理方程,注意方程增根的检验.
72199549530模块二:无理方程的根的讨论
模块二:无理方程的根的讨论
-201930147320知识精讲
知识精讲
3.增根的概念
-114300495300例题解析
例题解析
无理方程在化整式方程求解过程中,整式方程的解如果使得无理方程左右两边不相等,那么这个解就是方程的增根.
关于false的方程false有一个增根x=4,求:
a的值;
方程的根.
【难度】★★
【答案】(1)false;(2)false
【解析】(1)移项,两边平方得:false,移项得false,
两边平方得:false,将false代入有false,
整理得false,解得:false,false,当false时,false是方程增根,
当false时,false不是方程增根,由此即得false;
(2)将false代入上述平方整理的方程即有false,
移项整理得false,解得:false,false,
由题意可得false是原方程的增根,即得原方程的根是false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
若方程false有一个根是false,求实数m的值.
【难度】★★
【答案】false.
【解析】因为方程有一个根是false,所以代入得false,平方整理得false,
解得:false,false,经检验,false是方程的增根,应舍去,即得false.
【总结】考查无理方程根的意义,代入转化为其它未知数的求值即可.
若关于x的无理方程false有实数根,求k的取值范围.
【难度】★★★
【答案】false或false.
【解析】令false,则有false,原方程即为false,
整理即为false,当false时,则有false是增根,应舍去;
当false时,分解因式得false,解得:false(舍),false,
因为方程有实数根,则应有false,分类讨论得false或false,
即得false的取值范围为false或false.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性进行求解计算.
若关于x的方程false只有一个实数根,求m的取值范围.
【难度】★★★
【答案】false.
【解析】令false,则有false,原方程即为false,
整理即为false,
因为方程只有一个实数根,则方程有且仅有一根满足false,则另一根必满足false,
根据韦达定理可得:false,得false的取值范围是false.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性进行求解计算.
72199549530模块三:无理方程的应用
模块三:无理方程的应用
-201930233680知识精讲
知识精讲
4.应用
-68580233045例题解析
例题解析
寻找题目中的等量关系,列方程,求解,根据实际情况进行取舍.
用一根56厘米的细铁丝弯折成一个直角三角形,使它的一条直角边长为7厘米, 求这个直角三角形的另两条边的长度.
【难度】★★
【答案】false和false.
【解析】设另外一条直角边长为false,根据勾股定理可得斜边长为false,
依题意可得false,解得:false,经检验,false是原方程的根且符合
题意,则斜边长为false,即另两边长分别为false和false.
【总结】考查直角三角形勾股定理的应用,用周长列式解题,注意应用题也要验根.
建一块场地,用600块正方形的砖头铺成,如果把场地的面积扩大到原来面积的2 倍还多0.6平方米,且正方形的砖头的边长增加10厘米,则需要铺540块方砖,求原 场地的面积.
【难度】★★
【答案】false.
【解析】设原场地的边长为false,false,则扩大后场边长为false,
依题意得false,整理得false,
解得:false,false(舍),由此得原场地面积为false.
【总结】考查根据题意找准等量关系列方程解应用题,注意单位的统一.
若Q点在直线false上,且Q到点P(0,2)的距离为false,求Q点的坐标.
【难度】★★
【答案】false或false
【解析】设点false,由两点间距离公式,依题意可得false,
平方整理,得:false,解得:false,false,
经检验,false,false都是原方程的根,
由此代入即得false或false.
【总结】考查利用两点间距离公式的应用列方程,注意设出点的坐标.
37306251118235A
B
P
N
M
O
l1
l2
A
B
P
N
M
O
l1
l2
false与false为两条互相垂直的大路,小李和老王从十字路口O点同时出发,分别沿着 图示的方向以1千米/小时和2千米/小时的速度前进,到达A与B地,一座学校座落于 距false8千米,距false5千米的P处,问:经过多少时间,两人距离学校的路程刚好相等? 是几千米?
【难度】★★
【答案】经过false两人距离学校路程相等.
【解析】设经过false两人距离学校距离相等,即false,
则有false,false,false,false,
根据勾股定理,依题意可得:false,
平方整理得false,解得:false,false,
经检验,false,false都是原方程的根,但false不符合题意,应舍去,
即经过false两人距离学校路程相等.
【总结】考查利用勾股定理列方程,注意找准等量关系.
有一群蜜蜂,一部分飞进了枸杞里,其个数等于总数的一半的平方根,还有全体
的false遗留在后面,此外,这群里还有一个小蜜蜂在莲花旁徘徊着,它被一个坠入香花陷
阱的同伴的呻吟声所吸引.试问:这群蜜蜂共有多少个?
【难度】★★★
【答案】这群小蜜蜂共有72个.
【解析】设这群蜜蜂共有false个,根据蜂群总数,
依题意可得false,平方整理得false,解得:false,false,
经检验,false是原方程的增根,
即得这群小蜜蜂共有72个.
【总结】考查根据题意列方程解应用题,注意计算不要遗漏.
m、n为两段互相垂直的笔直的公路,工厂A在公路n上,距离公路m为1千米.工 厂B距离公路m为2千米,且距离公路n为3千米,现在要在公路m上选一个地址造 一个车站P,使它与A、B两厂的距离和为false千米,试指出车站P的位置?
【难度】★★★
350774034925A
B
n
m
A
B
n
m
【答案】车站false在两公路交点上方false或false处.
【解析】以直线false为false轴,以直线false为false轴,两直线交点为
坐标原点,建立平面直角坐标系,
依题意有false,false,设点false,
根据两点间距离公式,
依题意可得false,
二次平方后,整理得:false,解得:false,false,
经检验,false,false都是原方程的根,
即车站false在两公路交点上方false或false处.
【总结】考查利用建立平面直角坐标系确定点的位置问题.
如图,x轴表示一条东西方向的道路,y表示一条南北方向的道路,小丽和小明分 别从十字路口O点处同时出发,小丽沿着x轴以4千米/时的速度由西向东前进,小明 沿着y轴以5千米/时的速度由南向北前进,有一棵百年古树位于图中的P点处,古树 与x轴、y轴的距离分别是3千米和2千米,问:
离开路口后,经过多长时间,两人与古树的距离恰好相等?
离开路口后多少时间,两人与这课古树所处的位置恰好在一条直线上?
3571875144145A
B
y北
x东
西
南
P
O
A
B
y北
x东
西
南
P
O
【难度】★★★
【答案】(1)false;(2)false.
【解析】(1)建立如图的平面直角坐标系,设经过false两人与
古树距离相等,即false,则有false,false,false,根据两点间距离公式依题意可得:
false,
平方整理得:false,解得:false,false,
经检验,false,false都是原方程的根,但false不符合题意,应舍去,
即经过false两人距离古树距离相等;
设直线false解析式为false,则有false,解得:false,
即直线false解析式为false,两人与古树在同一直线上,即直线false过点false,代入直线解析式即得false,解得:false,
即离开false后两人与古树处于同一直线上.
【总结】考查对题目的理解,主要是转换到平面直角坐标系中进行解题.
随堂检测
随堂检测
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
【难度】★
【答案】D
【解析】根据无理方程的概念,方程中含有根式,并且被开方数是含有未知数的代数式的方
程叫做无理方程,可知D是无理方程,故选D.
【总结】考查无理方程的概念,方程中根号内含有未知数即可.
根据平方根的意义,直接判断下列方程是否有解,并简述理由:
(1)false; (2)false;
(3)false; (4)false.
【难度】★
【答案】(2)有解,(1)、(3)、(4)无解.
【解析】根据二次根式的双重非负性,对(1),false,故方程无实数解;
对(2),由false,即有false,false,可知方程有实数解;
对(3),false,false无解,即方程无实数解;对(4),false,false无解,
即方程无实数解.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行初步判定.
方程false的实数解为( ).
A.false B.false C.false D.false
【难度】★
【答案】C
【解析】false,可知false,得false,故选C.
【总结】考查根据二次根式的性质判定方程解的情况.
用换元法解方程false时,设false.则该方程 可转换成整式方程是_________.
【难度】★
【答案】false.
【解析】由false,可得:false,原方程即为false,
整理即为false.
【总结】考查用“换元法”对无理方程进行变形转化,注意最终要化成整式方程.
解方程:
(1)false; (2)false.
【难度】★
【答案】(1)false;(2)false.
【解析】(1)移项两边平方得:false,整理得:false,
因式分解法解得false,false,经检验,false是原方程的增根,
即原方程的根为false;
(2)移项得false,两边平方得false,整理得:false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false,false.
【解析】(1)移项得false,两边平方得false,
移项得false,两边平方整理得false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false;
(2)移项两边平方得false,移项得false,
两边平方整理得false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
解方程:
(1)false;
(2)false.
【难度】★★
【答案】(1)false,false;(2)false,false.
【解析】(1)令false,得false,方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根;
(2)令false,得false,原方程即false,
解得:false(舍),false,令false,平方整理得false,
解得:false,false,经检验,false,false都是原方程的根.
【总结】考查用“换元法”解无理方程,注意根据二次根式的非负性舍去相应增根.
有两块正方形木板,其中大的一块木板面积比小的木板面积大45平方米,小的木
板的边长比大的木板的边长短3分米,求这块小木板的面积.
【难度】★★
【答案】小木板面积为false.
【解析】设小木板面积为false,则大木板面积为false,由false,
依题意可得false,移项整理得false,即得:false,
经检验,false是原方程的根,即小木板面积为false.
【总结】考查根据题意列方程解应用题,注意题目中的单位换算.
如果false轴上一点P到两点A(3,5)、B(-1,-2)的距离相等,求P点的坐标.
【难度】★★
【答案】false.
【解析】设点false,根据两点间距离公式依题意可得false,
平方得false,解得:false,经检验,false是原方程的根,
即false.
【总结】考查利用两点间距离公式确定点的位置问题.
解方程:false.
【难度】★★
【答案】false.
【解析】false,
根据题意,得false,可得false,
两式相加可得false,平方整理得false,解得:false,false,
经检验,false是原方程的增根,即原方程的根是false.
【总结】考查有特殊形式的无理方程的解法,注意观察好含未知数的根式之间的关联.
解方程:false.
【难度】★★★
【答案】false.
【解析】令false,则false,原方程即为false,
解得:false,false(舍),则有false,
解得:false,经检验,false是原方程的根.
【总结】考查利用“换元法”解无理方程,注意观察两个无理式之间的关联.
已知a为非负整数,若关于x的方程false至少有一个整数根,
求a的值.
【难度】★★★
【答案】false或false.
【解析】令false,则有false,原方程即为false,
得false,由false,可得false,则有false,因为false为整数,
则false为整数,同时false为整数,则false必为有理数,由此可得:false或false,
当false时,得false;当false时,得false;综上,false或6.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性和题目要求求解计算
4686300562610A地在M地的正北方向12千米处,B地在M地的正东方向12千米处,某人从 B地出发向正西方向行至C地,再沿CA方向到达A地,这样比由B地到M地再到A 地的路程少4千米,求M地与C地之间的距离.
【难度】★★★
【答案】false.
【解析】如图建立平面平面直角坐标系,点false为原点,则有false,false,
设false,根据两点间距离公式false,
依题意可得false,移项得false,解得:false,
经检验,false是原方程的根,即得false.
【总结】考查根据构造平面直角坐标系解方程问题.
-1143005080课后作业
课后作业
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
【难度】★
【答案】B
【解析】根据无理方程的概念,方程中含有根式,并且被开方数是含有未知数的代数式的方
程叫做无理方程,可知B是无理方程,故选B.
【总结】考查无理方程的概念,方程中根号内含有未知数即可
下列无理方程有解的方程是( ).
A.false B.false
C.false D.false
【难度】★
【答案】B
【解析】根据二次根式的双重非负性,对A选项,false,故方程无实数解;
对C选项,false,不可能同时成立,可知方程无实数解;对D选项,false,
false无解,即方程无实数解;故选B.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行初步判定.
下列四个无理方程中,有一个根是x=2的方程是( ).
A.false B.false
C.false D.false
【难度】★
【答案】C
【解析】对A、B、D选项,将false代入原方程,左边false右边,可知false不是相应方程的
解;对C选项,左边false右边,可知false是相应方程的解,故选C.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行初步判定.
用换元法解false方程时,设false=y,则原方程可转换成整式方程_____________.
【难度】★
【答案】false.
【解析】由false,可得false,原方程即为false,
整理即为false.
【总结】考查用“换元法”对无理方程进行变形转化,注意最终化成整式方程的形式.
将下列方程化成有理方程:
(1)false; (2)false; (3)false.
【难度】★
【答案】(1)false;(2)false;(3)false.
【解析】(1)移项得false,两边平方整理得false;
(2)移项得false,两边平方得false,整理得false;
(3)移项得false,两边平方得false,移项得false,
平方整理得:false.
【总结】考查无理方程转化为有理方程,移项平方即可.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方得:false,整理得false,
因式分解法,解得:false,false,经检验,false是原方程的增根,
即原方程的根为false;
(2)移项得false,两边平方得false,整理得:false,
解得:false,false,经检验,false是原方程的增根,
即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false,false.
【解析】(1)两边平方得false,整理得:false,
因式分解法,解得:false,false,经检验,false是原方程的增根,
即原方程的根为false;
(2)移项得false,两边平方得false,整理得:false,
解得:false,false,经检验,false,false都是原方程的根.
【总结】考查无理方程的解法,注意方程增根的检验.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)移项得false,两边平方,得:false,
移项得false,两边平方整理,得false,解得:false,
经检验,false是原方程的根,即原方程的根为false;
(2)移项得false,两边平方,得:false,
移项得false,两边平方整理得,false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可
有一个数,它的平方根比它的倒数的正平方根的3倍多2,求这个数.
【难度】★★
【答案】9.
【解析】设这个数为false,依题意可得false,平方得:false,
整理得false,解得:false,false,经检验,false是原方程的增根,
得方程的根是false,即这个数是9.
【总结】考查根据题意列方程解题,注意无理方程增根的检验.
已知点P是x轴上一点,它与点A(-9,3)之间的距离是15,求点P的坐标.
【难度】★★
【答案】false或false
【解析】设点false,根据两点间距离公式,依题意可得false,
平方得false,解得:false,false,
经检验,false,false是原方程的根,
即false或false.
【总结】考查利用两点间距离公式确定点的位置问题
某学校修建两块面积相等的绿地,一块是长方形,另一块是正方形.已知长方形绿地的长比宽多14米,且这两块绿地的周长之和为196米,那么长方形绿地的宽是多少?
【难度】★★
【答案】false.
【解析】设长方形绿地宽为false,则长为false,根据相关周长和面积公式,
依题意可得false,移项得false,
平方整理得:false,解得:false,
经检验,false是原方程的根,
即长方形绿地宽为false.
【总结】考查长方形和正方形周长面积公式的综合应用,根据相关公式列出方程解题.
解下列方程:
(1)false; (2)false.
【难度】★★★
【答案】(1)false,false;(2)false,false.
【解析】(1)令false,得false,方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根;
(2)令false,得:false,
展开完全平方原方程即为false,解得:false(舍),false,
令false,平方整理,得false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查用“换元法”解无理方程,注意元的取值范围.
解下列关于false的方程:
(1)false; (2)false.
【难度】★★★
【答案】(1)false;(2)false.
【解析】(1)两边平方,得:false,
移项得false,两边平方,得:false,
整理得false,解得:false,false,
经检验,false是原方程的增根,
即原方程的根为false;
(2)两边平方,得:false,
移项得false,两边平方得false,
整理得:false,解得:false,false,
经检验,false是原方程的增根,
即原方程的根为false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可,注意检验增根.
若关于x的方程false有实数根,求k的取值范围.
【难度】★★★
【答案】false.
【解析】令false,则有false,原方程即为false,
整理即为false,因为方程有实数根,则有false,
得false,且方程至少有一根满足false,
根据韦达定理可得:false,可知方程两根必为一非负根一负根,
则有false,得:false,即false的取值范围是false.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性结合题意求解计算.
教师
日期
学生
课程编号
课型
同步/专题
课题
无理方程及应用
教学目标
理解无理方程的概念;掌握简单的无理方程的解法,知道“验根”是解无理方程的必要步骤,掌握验根的基本方法.
熟练的解决无理方程的应用问题.
教学重点
1.无理方程的解法;
2.无理方程有可能产生增根的理解.
教学安排
版块
时长
1
无理方程的概念及解法
50分钟
2
无理方程的应用
30分钟
3
课堂练习
40分钟
1111250146050无理方程
无理方程
-37147516510 知识结构
知识结构
386080147955模块一:无理方程的概念和解法
模块一:无理方程的概念和解法
-2171705080知识精讲
知识精讲
1.无理方程的概念
方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程.
2.解无理方程的方法
通过平方把无理方程转化为整式方程,再求解.
3.解无理方程的一般步骤
(1)方程两边平方,化成整式方程;
(2)解这个整式方程,求出整式方程的根;
(3)检验.直接代入原方程中,看其是否成立.如果成立,则这个根为原方程的根,从而解出原方程的解;如果不成立,则这个根为增根,方程无解.
-60325-154940例题解析
例题解析
下列方程是哪些是关于false的无理方程?
(1)false; (2)false; (3)false;
(4)false; (5)false; (6)false.
下列哪个方程有实数解( )
A.false B.false
C.false D.false
若方程false有解,则false的取值范围是________.
不解方程,说明下列方程是否有实数根:
(1)false;
(2)false.
用换元法解方程false时,设false.则该方程转换整式方程是____________.
解下列方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false;
解下列方程:
(1)false; (2)false.
解方程:false.
解方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false.
解下列方程:false.
解下列方程:false.
72199549530模块二:无理方程的根的讨论
模块二:无理方程的根的讨论
-201930147320知识精讲
知识精讲
3.增根的概念
-114300495300例题解析
例题解析
无理方程在化整式方程求解过程中,整式方程的解如果使得无理方程左右两边不相等,那么这个解就是方程的增根.
关于false的方程false有一个增根x=4,求:
a的值;
方程的根.
若方程false有一个根是false,求实数m的值.
若关于x的无理方程false有实数根,求k的取值范围.
若关于x的方程false只有一个实数根,求m的取值范围.
72199549530模块三:无理方程的应用
模块三:无理方程的应用
-201930233680知识精讲
知识精讲
4.应用
-68580233045例题解析
例题解析
寻找题目中的等量关系,列方程,求解,根据实际情况进行取舍.
用一根56厘米的细铁丝弯折成一个直角三角形,使它的一条直角边长为7厘米, 求这个直角三角形的另两条边的长度.
建一块场地,用600块正方形的砖头铺成,如果把场地的面积扩大到原来面积的2 倍还多0.6平方米,且正方形的砖头的边长增加10厘米,则需要铺540块方砖,求原 场地的面积.
若Q点在直线false上,且Q到点P(0,2)的距离为false,求Q点的坐标.
37306251118235A
B
P
N
M
O
l1
l2
A
B
P
N
M
O
l1
l2
false与false为两条互相垂直的大路,小李和老王从十字路口O点同时出发,分别沿着 图示的方向以1千米/小时和2千米/小时的速度前进,到达A与B地,一座学校座落于 距false8千米,距false5千米的P处,问:经过多少时间,两人距离学校的路程刚好相等? 是几千米?
有一群蜜蜂,一部分飞进了枸杞里,其个数等于总数的一半的平方根,还有全体
的false遗留在后面,此外,这群里还有一个小蜜蜂在莲花旁徘徊着,它被一个坠入香花陷
阱的同伴的呻吟声所吸引.试问:这群蜜蜂共有多少个?
m、n为两段互相垂直的笔直的公路,工厂A在公路n上,距离公路m为1千米.工 厂B距离公路m为2千米,且距离公路n为3千米,现在要在公路m上选一个地址造 一个车站P,使它与A、B两厂的距离和为false千米,试指出车站P的位置?
如图,x轴表示一条东西方向的道路,y表示一条南北方向的道路,小丽和小明分 别从十字路口O点处同时出发,小丽沿着x轴以4千米/时的速度由西向东前进,小明 沿着y轴以5千米/时的速度由南向北前进,有一棵百年古树位于图中的P点处,古树 与x轴、y轴的距离分别是3千米和2千米,问:
离开路口后,经过多长时间,两人与古树的距离恰好相等?
离开路口后多少时间,两人与这课古树所处的位置恰好在一条直线上?
随堂检测
随堂检测
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
根据平方根的意义,直接判断下列方程是否有解,并简述理由:
(1)false; (2)false;
(3)false; (4)false.
方程false的实数解为( ).
A.false B.false C.false D.false
用换元法解方程false时,设false.则该方程 可转换成整式方程是_________.
解方程:
(1)false; (2)false.
解方程:
(1)false; (2)false.
解方程:
(1)false;
(2)false.
有两块正方形木板,其中大的一块木板面积比小的木板面积大45平方米,小的木板的边长比大的木板的边长短3分米,求这块小木板的面积.
如果false轴上一点P到两点A(3,5)、B(-1,-2)的距离相等,求P点的坐标.
解方程:false.
解方程:false.
已知a为非负整数,若关于x的方程false至少有一个整数根,
求a的值.
4686300562610A地在M地的正北方向12千米处,B地在M地的正东方向12千米处,某人从 B地出发向正西方向行至C地,再沿CA方向到达A地,这样比由B地到M地再到A 地的路程少4千米,求M地与C地之间的距离.
-1143005080课后作业
课后作业
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
下列无理方程有解的方程是( ).
A.false B.false
C.false D.false
下列四个无理方程中,有一个根是x=2的方程是( ).
A.false B.false
C.false D.false
用换元法解false方程时,设false=y,则原方程可转换成整式方程_____________.
将下列方程化成有理方程:
(1)false; (2)false; (3)false.
解下列方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false.
解下列方程:
(1)false; (2)false.
有一个数,它的平方根比它的倒数的正平方根的3倍多2,求这个数.
已知点P是x轴上一点,它与点A(-9,3)之间的距离是15,求点P的坐标.
某学校修建两块面积相等的绿地,一块是长方形,另一块是正方形.已知长方形绿地的长比宽多14米,且这两块绿地的周长之和为196米,那么长方形绿地的宽是多少?
解下列方程:
(1)false; (2)false.
解下列关于false的方程:
(1)false; (2)false.
若关于x的方程false有实数根,求k的取值范围.
1047750010617200初二数学寒假班(教师版)
教师
日期
学生
课程编号
课型
同步/专题
课题
无理方程及应用
教学目标
理解无理方程的概念;掌握简单的无理方程的解法,知道“验根”是解无理方程的必要步骤,掌握验根的基本方法.
熟练的解决无理方程的应用问题.
教学重点
1.无理方程的解法;
2.无理方程有可能产生增根的理解.
教学安排
版块
时长
1
无理方程的概念及解法
50分钟
2
无理方程的应用
30分钟
3
课堂练习
40分钟
1111250146050无理方程
无理方程
-37147516510 知识结构
知识结构
386080147955模块一:无理方程的概念和解法
模块一:无理方程的概念和解法
-2171705080知识精讲
知识精讲
1.无理方程的概念
方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程.
2.解无理方程的方法
通过平方把无理方程转化为整式方程,再求解.
3.解无理方程的一般步骤
(1)方程两边平方,化成整式方程;
(2)解这个整式方程,求出整式方程的根;
(3)检验.直接代入原方程中,看其是否成立.如果成立,则这个根为原方程的根,从而解出原方程的解;如果不成立,则这个根为增根,方程无解.
-60325-154940例题解析
例题解析
下列方程是哪些是关于false的无理方程?
(1)false; (2)false; (3)false;
(4)false; (5)false; (6)false.
【难度】★
【答案】(1)、(2)、(3)、(4)、(6)是无理方程.
【解析】根据无理方程的概念,方程中含有根式,并且被开方数是含有未知数的代数式的方
程叫做无理方程,可知(1)、(2)、(4)、(6)都是无理方程,false,可知(3)也
是无理方程.
【总结】考查无理方程的概念,方程中根号内含有未知数即可.
下列哪个方程有实数解( )
A.false B.false
C.false D.false
【难度】★
【答案】D
【解析】根据二次根式的双重非负性,对A选项,false,此时false,故方程
无实数解;对B选项,false,可知方程无实数解;对C选项,false,
false无解,即方程无实数解;故选D.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行简单判定.
若方程false有解,则false的取值范围是________.
【难度】★
【答案】false.
【解析】移项得false,方程有解,根据二次根式的非负性,可得false,得false.
【总结】考查无理方程有解的应用,根据二次根式的非负性即可进行判断.
不解方程,说明下列方程是否有实数根:
(1)false;
(2)false.
【难度】★
【答案】(1)有唯一实数根false;
(2)当false时,方程无实数根;当false时,方程有无数个实数根.
【解析】(1)根据二次根式的非负性,可得:false,即得false的定义域为false,
此时false,即得方程有唯一实数根false;
当false时,则有false,根据二次根式非负性,可知方程无实数根;
当false时,等式恒成立,可知方程有无数实数根,满足false即可.
【总结】考查对无理方程解的判断,对部分方程根据二次根式双重非负性即可进行判定.
用换元法解方程false时,设false.则该方程转换整式方程是____________.
【难度】★
【答案】false.
【解析】由false,可得false,原方程即为false,
整理即为false.
【总结】考查用“换元法”对无理方程进行变形转化,注意最终要化成整式形式.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方,得:false,整理得:false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false;
移项得:false,两边平方得:false,
因式分解整理得:false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解下列方程:
(1)false; (2)false;
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方,得:false,整理得:false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false;
(2)由原式得:false或false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意无理方程的验根.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方得:false,整理得:false,
配方法解得:false,false,
经检验,false是原方程的增根,即原方程的根为false;
(2)移项得false,两边平方得false,整理得false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解方程:false.
【难度】★★
【答案】false,false.
【解析】令false,则false,原方程即为false,解得:false,false,
则有false或false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查利用“换元法”解无理方程,注意观察无理方程含未知数的根式之间的联系.
解方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false,false;(2)false,false.
【解析】(1)令false,得false,原方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根;
(2)令false,得false,原方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查用“换元法”解无理方程,注意根据元的取值范围舍去增根.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)移项得false,两边平方得false,
移项得false,两边平方得false,解得:false,
经检验,false是原方程的根;
(2)两边平方得false,移项得false,
两边平方整理得false,配方法解得:false,false,
经检验,false是原方程的增根,即原方程的根是false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
解下列方程:false.
【难度】★★★
【答案】false.
【解析】平方得false,移项得false,
两边平方整理得false,解得:false,false,
经检验,false是原方程的增根,即原方程的根是false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
解下列方程:false.
【难度】★★★
【答案】false.
【解析】令false,则有false,由此原方程可变形得:
false,整理即为false,
因式分解法解得:false,false,即false或false,
由false,整理得false,解得:false,false,
经检验,false是原方程的增根,
由false,可解得:false,经检验,false是原方程的增根,
综上所述,原方程的根是false.
【总结】考查较复杂的换元法的转化解无理方程,注意方程增根的检验.
72199549530模块二:无理方程的根的讨论
模块二:无理方程的根的讨论
-201930147320知识精讲
知识精讲
3.增根的概念
-114300495300例题解析
例题解析
无理方程在化整式方程求解过程中,整式方程的解如果使得无理方程左右两边不相等,那么这个解就是方程的增根.
关于false的方程false有一个增根x=4,求:
a的值;
方程的根.
【难度】★★
【答案】(1)false;(2)false
【解析】(1)移项,两边平方得:false,移项得false,
两边平方得:false,将false代入有false,
整理得false,解得:false,false,当false时,false是方程增根,
当false时,false不是方程增根,由此即得false;
(2)将false代入上述平方整理的方程即有false,
移项整理得false,解得:false,false,
由题意可得false是原方程的增根,即得原方程的根是false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
若方程false有一个根是false,求实数m的值.
【难度】★★
【答案】false.
【解析】因为方程有一个根是false,所以代入得false,平方整理得false,
解得:false,false,经检验,false是方程的增根,应舍去,即得false.
【总结】考查无理方程根的意义,代入转化为其它未知数的求值即可.
若关于x的无理方程false有实数根,求k的取值范围.
【难度】★★★
【答案】false或false.
【解析】令false,则有false,原方程即为false,
整理即为false,当false时,则有false是增根,应舍去;
当false时,分解因式得false,解得:false(舍),false,
因为方程有实数根,则应有false,分类讨论得false或false,
即得false的取值范围为false或false.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性进行求解计算.
若关于x的方程false只有一个实数根,求m的取值范围.
【难度】★★★
【答案】false.
【解析】令false,则有false,原方程即为false,
整理即为false,
因为方程只有一个实数根,则方程有且仅有一根满足false,则另一根必满足false,
根据韦达定理可得:false,得false的取值范围是false.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性进行求解计算.
72199549530模块三:无理方程的应用
模块三:无理方程的应用
-201930233680知识精讲
知识精讲
4.应用
-68580233045例题解析
例题解析
寻找题目中的等量关系,列方程,求解,根据实际情况进行取舍.
用一根56厘米的细铁丝弯折成一个直角三角形,使它的一条直角边长为7厘米, 求这个直角三角形的另两条边的长度.
【难度】★★
【答案】false和false.
【解析】设另外一条直角边长为false,根据勾股定理可得斜边长为false,
依题意可得false,解得:false,经检验,false是原方程的根且符合
题意,则斜边长为false,即另两边长分别为false和false.
【总结】考查直角三角形勾股定理的应用,用周长列式解题,注意应用题也要验根.
建一块场地,用600块正方形的砖头铺成,如果把场地的面积扩大到原来面积的2 倍还多0.6平方米,且正方形的砖头的边长增加10厘米,则需要铺540块方砖,求原 场地的面积.
【难度】★★
【答案】false.
【解析】设原场地的边长为false,false,则扩大后场边长为false,
依题意得false,整理得false,
解得:false,false(舍),由此得原场地面积为false.
【总结】考查根据题意找准等量关系列方程解应用题,注意单位的统一.
若Q点在直线false上,且Q到点P(0,2)的距离为false,求Q点的坐标.
【难度】★★
【答案】false或false
【解析】设点false,由两点间距离公式,依题意可得false,
平方整理,得:false,解得:false,false,
经检验,false,false都是原方程的根,
由此代入即得false或false.
【总结】考查利用两点间距离公式的应用列方程,注意设出点的坐标.
37306251118235A
B
P
N
M
O
l1
l2
A
B
P
N
M
O
l1
l2
false与false为两条互相垂直的大路,小李和老王从十字路口O点同时出发,分别沿着 图示的方向以1千米/小时和2千米/小时的速度前进,到达A与B地,一座学校座落于 距false8千米,距false5千米的P处,问:经过多少时间,两人距离学校的路程刚好相等? 是几千米?
【难度】★★
【答案】经过false两人距离学校路程相等.
【解析】设经过false两人距离学校距离相等,即false,
则有false,false,false,false,
根据勾股定理,依题意可得:false,
平方整理得false,解得:false,false,
经检验,false,false都是原方程的根,但false不符合题意,应舍去,
即经过false两人距离学校路程相等.
【总结】考查利用勾股定理列方程,注意找准等量关系.
有一群蜜蜂,一部分飞进了枸杞里,其个数等于总数的一半的平方根,还有全体
的false遗留在后面,此外,这群里还有一个小蜜蜂在莲花旁徘徊着,它被一个坠入香花陷
阱的同伴的呻吟声所吸引.试问:这群蜜蜂共有多少个?
【难度】★★★
【答案】这群小蜜蜂共有72个.
【解析】设这群蜜蜂共有false个,根据蜂群总数,
依题意可得false,平方整理得false,解得:false,false,
经检验,false是原方程的增根,
即得这群小蜜蜂共有72个.
【总结】考查根据题意列方程解应用题,注意计算不要遗漏.
m、n为两段互相垂直的笔直的公路,工厂A在公路n上,距离公路m为1千米.工 厂B距离公路m为2千米,且距离公路n为3千米,现在要在公路m上选一个地址造 一个车站P,使它与A、B两厂的距离和为false千米,试指出车站P的位置?
【难度】★★★
350774034925A
B
n
m
A
B
n
m
【答案】车站false在两公路交点上方false或false处.
【解析】以直线false为false轴,以直线false为false轴,两直线交点为
坐标原点,建立平面直角坐标系,
依题意有false,false,设点false,
根据两点间距离公式,
依题意可得false,
二次平方后,整理得:false,解得:false,false,
经检验,false,false都是原方程的根,
即车站false在两公路交点上方false或false处.
【总结】考查利用建立平面直角坐标系确定点的位置问题.
如图,x轴表示一条东西方向的道路,y表示一条南北方向的道路,小丽和小明分 别从十字路口O点处同时出发,小丽沿着x轴以4千米/时的速度由西向东前进,小明 沿着y轴以5千米/时的速度由南向北前进,有一棵百年古树位于图中的P点处,古树 与x轴、y轴的距离分别是3千米和2千米,问:
离开路口后,经过多长时间,两人与古树的距离恰好相等?
离开路口后多少时间,两人与这课古树所处的位置恰好在一条直线上?
3571875144145A
B
y北
x东
西
南
P
O
A
B
y北
x东
西
南
P
O
【难度】★★★
【答案】(1)false;(2)false.
【解析】(1)建立如图的平面直角坐标系,设经过false两人与
古树距离相等,即false,则有false,false,false,根据两点间距离公式依题意可得:
false,
平方整理得:false,解得:false,false,
经检验,false,false都是原方程的根,但false不符合题意,应舍去,
即经过false两人距离古树距离相等;
设直线false解析式为false,则有false,解得:false,
即直线false解析式为false,两人与古树在同一直线上,即直线false过点false,代入直线解析式即得false,解得:false,
即离开false后两人与古树处于同一直线上.
【总结】考查对题目的理解,主要是转换到平面直角坐标系中进行解题.
随堂检测
随堂检测
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
【难度】★
【答案】D
【解析】根据无理方程的概念,方程中含有根式,并且被开方数是含有未知数的代数式的方
程叫做无理方程,可知D是无理方程,故选D.
【总结】考查无理方程的概念,方程中根号内含有未知数即可.
根据平方根的意义,直接判断下列方程是否有解,并简述理由:
(1)false; (2)false;
(3)false; (4)false.
【难度】★
【答案】(2)有解,(1)、(3)、(4)无解.
【解析】根据二次根式的双重非负性,对(1),false,故方程无实数解;
对(2),由false,即有false,false,可知方程有实数解;
对(3),false,false无解,即方程无实数解;对(4),false,false无解,
即方程无实数解.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行初步判定.
方程false的实数解为( ).
A.false B.false C.false D.false
【难度】★
【答案】C
【解析】false,可知false,得false,故选C.
【总结】考查根据二次根式的性质判定方程解的情况.
用换元法解方程false时,设false.则该方程 可转换成整式方程是_________.
【难度】★
【答案】false.
【解析】由false,可得:false,原方程即为false,
整理即为false.
【总结】考查用“换元法”对无理方程进行变形转化,注意最终要化成整式方程.
解方程:
(1)false; (2)false.
【难度】★
【答案】(1)false;(2)false.
【解析】(1)移项两边平方得:false,整理得:false,
因式分解法解得false,false,经检验,false是原方程的增根,
即原方程的根为false;
(2)移项得false,两边平方得false,整理得:false,
解得:false,false,经检验,false是原方程的增根,即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false,false.
【解析】(1)移项得false,两边平方得false,
移项得false,两边平方整理得false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false;
(2)移项两边平方得false,移项得false,
两边平方整理得false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可.
解方程:
(1)false;
(2)false.
【难度】★★
【答案】(1)false,false;(2)false,false.
【解析】(1)令false,得false,方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根;
(2)令false,得false,原方程即false,
解得:false(舍),false,令false,平方整理得false,
解得:false,false,经检验,false,false都是原方程的根.
【总结】考查用“换元法”解无理方程,注意根据二次根式的非负性舍去相应增根.
有两块正方形木板,其中大的一块木板面积比小的木板面积大45平方米,小的木
板的边长比大的木板的边长短3分米,求这块小木板的面积.
【难度】★★
【答案】小木板面积为false.
【解析】设小木板面积为false,则大木板面积为false,由false,
依题意可得false,移项整理得false,即得:false,
经检验,false是原方程的根,即小木板面积为false.
【总结】考查根据题意列方程解应用题,注意题目中的单位换算.
如果false轴上一点P到两点A(3,5)、B(-1,-2)的距离相等,求P点的坐标.
【难度】★★
【答案】false.
【解析】设点false,根据两点间距离公式依题意可得false,
平方得false,解得:false,经检验,false是原方程的根,
即false.
【总结】考查利用两点间距离公式确定点的位置问题.
解方程:false.
【难度】★★
【答案】false.
【解析】false,
根据题意,得false,可得false,
两式相加可得false,平方整理得false,解得:false,false,
经检验,false是原方程的增根,即原方程的根是false.
【总结】考查有特殊形式的无理方程的解法,注意观察好含未知数的根式之间的关联.
解方程:false.
【难度】★★★
【答案】false.
【解析】令false,则false,原方程即为false,
解得:false,false(舍),则有false,
解得:false,经检验,false是原方程的根.
【总结】考查利用“换元法”解无理方程,注意观察两个无理式之间的关联.
已知a为非负整数,若关于x的方程false至少有一个整数根,
求a的值.
【难度】★★★
【答案】false或false.
【解析】令false,则有false,原方程即为false,
得false,由false,可得false,则有false,因为false为整数,
则false为整数,同时false为整数,则false必为有理数,由此可得:false或false,
当false时,得false;当false时,得false;综上,false或6.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性和题目要求求解计算
4686300562610A地在M地的正北方向12千米处,B地在M地的正东方向12千米处,某人从 B地出发向正西方向行至C地,再沿CA方向到达A地,这样比由B地到M地再到A 地的路程少4千米,求M地与C地之间的距离.
【难度】★★★
【答案】false.
【解析】如图建立平面平面直角坐标系,点false为原点,则有false,false,
设false,根据两点间距离公式false,
依题意可得false,移项得false,解得:false,
经检验,false是原方程的根,即得false.
【总结】考查根据构造平面直角坐标系解方程问题.
-1143005080课后作业
课后作业
下列方程是无理方程的是( ).
A.false B.false
C.false D.false
【难度】★
【答案】B
【解析】根据无理方程的概念,方程中含有根式,并且被开方数是含有未知数的代数式的方
程叫做无理方程,可知B是无理方程,故选B.
【总结】考查无理方程的概念,方程中根号内含有未知数即可
下列无理方程有解的方程是( ).
A.false B.false
C.false D.false
【难度】★
【答案】B
【解析】根据二次根式的双重非负性,对A选项,false,故方程无实数解;
对C选项,false,不可能同时成立,可知方程无实数解;对D选项,false,
false无解,即方程无实数解;故选B.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行初步判定.
下列四个无理方程中,有一个根是x=2的方程是( ).
A.false B.false
C.false D.false
【难度】★
【答案】C
【解析】对A、B、D选项,将false代入原方程,左边false右边,可知false不是相应方程的
解;对C选项,左边false右边,可知false是相应方程的解,故选C.
【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行初步判定.
用换元法解false方程时,设false=y,则原方程可转换成整式方程_____________.
【难度】★
【答案】false.
【解析】由false,可得false,原方程即为false,
整理即为false.
【总结】考查用“换元法”对无理方程进行变形转化,注意最终化成整式方程的形式.
将下列方程化成有理方程:
(1)false; (2)false; (3)false.
【难度】★
【答案】(1)false;(2)false;(3)false.
【解析】(1)移项得false,两边平方整理得false;
(2)移项得false,两边平方得false,整理得false;
(3)移项得false,两边平方得false,移项得false,
平方整理得:false.
【总结】考查无理方程转化为有理方程,移项平方即可.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)两边平方得:false,整理得false,
因式分解法,解得:false,false,经检验,false是原方程的增根,
即原方程的根为false;
(2)移项得false,两边平方得false,整理得:false,
解得:false,false,经检验,false是原方程的增根,
即原方程的根为false.
【总结】考查无理方程的解法,注意方程增根的检验.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false,false.
【解析】(1)两边平方得false,整理得:false,
因式分解法,解得:false,false,经检验,false是原方程的增根,
即原方程的根为false;
(2)移项得false,两边平方得false,整理得:false,
解得:false,false,经检验,false,false都是原方程的根.
【总结】考查无理方程的解法,注意方程增根的检验.
解下列方程:
(1)false; (2)false.
【难度】★★
【答案】(1)false;(2)false.
【解析】(1)移项得false,两边平方,得:false,
移项得false,两边平方整理,得false,解得:false,
经检验,false是原方程的根,即原方程的根为false;
(2)移项得false,两边平方,得:false,
移项得false,两边平方整理得,false,解得:false,false,
经检验,false是原方程的增根,即原方程的根为false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可
有一个数,它的平方根比它的倒数的正平方根的3倍多2,求这个数.
【难度】★★
【答案】9.
【解析】设这个数为false,依题意可得false,平方得:false,
整理得false,解得:false,false,经检验,false是原方程的增根,
得方程的根是false,即这个数是9.
【总结】考查根据题意列方程解题,注意无理方程增根的检验.
已知点P是x轴上一点,它与点A(-9,3)之间的距离是15,求点P的坐标.
【难度】★★
【答案】false或false
【解析】设点false,根据两点间距离公式,依题意可得false,
平方得false,解得:false,false,
经检验,false,false是原方程的根,
即false或false.
【总结】考查利用两点间距离公式确定点的位置问题
某学校修建两块面积相等的绿地,一块是长方形,另一块是正方形.已知长方形绿地的长比宽多14米,且这两块绿地的周长之和为196米,那么长方形绿地的宽是多少?
【难度】★★
【答案】false.
【解析】设长方形绿地宽为false,则长为false,根据相关周长和面积公式,
依题意可得false,移项得false,
平方整理得:false,解得:false,
经检验,false是原方程的根,
即长方形绿地宽为false.
【总结】考查长方形和正方形周长面积公式的综合应用,根据相关公式列出方程解题.
解下列方程:
(1)false; (2)false.
【难度】★★★
【答案】(1)false,false;(2)false,false.
【解析】(1)令false,得false,方程即false,
整理得false,解得:false(舍),false,
令false,平方整理得false,解得:false,false,
经检验,false,false都是原方程的根;
(2)令false,得:false,
展开完全平方原方程即为false,解得:false(舍),false,
令false,平方整理,得false,解得:false,false,
经检验,false,false都是原方程的根.
【总结】考查用“换元法”解无理方程,注意元的取值范围.
解下列关于false的方程:
(1)false; (2)false.
【难度】★★★
【答案】(1)false;(2)false.
【解析】(1)两边平方,得:false,
移项得false,两边平方,得:false,
整理得false,解得:false,false,
经检验,false是原方程的增根,
即原方程的根为false;
(2)两边平方,得:false,
移项得false,两边平方得false,
整理得:false,解得:false,false,
经检验,false是原方程的增根,
即原方程的根为false.
【总结】考查含有多个二次根式的无理方程的解法,两边多次平方即可,注意检验增根.
若关于x的方程false有实数根,求k的取值范围.
【难度】★★★
【答案】false.
【解析】令false,则有false,原方程即为false,
整理即为false,因为方程有实数根,则有false,
得false,且方程至少有一根满足false,
根据韦达定理可得:false,可知方程两根必为一非负根一负根,
则有false,得:false,即false的取值范围是false.
【总结】考查无理方程根的判定,利用换元法根据二次根式的非负性结合题意求解计算.
同课章节目录
