沪教版(上海)八年级寒假班讲义——04函数的复习(含答案)
文档属性
| 名称 | 沪教版(上海)八年级寒假班讲义——04函数的复习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 21:36:13 | ||
图片预览



文档简介
初二数学寒假班(学生版)
教师
日期
学生
课程编号
课型 新课
课题 函数的复习
教学目标
熟悉正反比例及一次函数的概念和性质 能利用函数的性质解决相应的问题即求角或者边之间的关系
能够运动数形结合的思想解决几何背景下的函数问题.
教学重点
熟练的运用函数的性质
运用一次函数模型解决实际问题.
运用一次函数的图像与性质求解初步几何问题.
教学安排
版块 时长
1 正反比例函数 20min
2 一次函数 30min
3 函数的综合 50min
4 作业 20min
正比例函数:y=kx(k≠0);图像是一条直线,与坐标轴仅有一个交点;k>0时,随着x
的逐渐增大,函数值y的值越来越大;k<0时,随着x的逐渐增大,函数值y的值越来
越小.
反比例函数:(k≠0),图像是双曲线,与坐标轴无交点;k>0时,在每一象限内,
随着x的逐渐增大,函数值y的值越来越小;k<0时,在每一象限内,随着x的逐渐增
大,函数值y的值越来越大.
(1)正方形的周长c与正方形的对角线长a_______正比例(填“成”或“不成”);
(2)已知正比例函数的自变量x减少2时,对应函数的值增加3,则这个函数的解析式为________________.
(1)如果y=kx+2k+x是正比例函数,求k的值;
(2)如果是反比例函数,求m的值.
(1)正比例函数经过第___________象限,y随x增大而_________;
(2)反比例函数经过第___________象限,在同一象限内,y随x增大而_________.
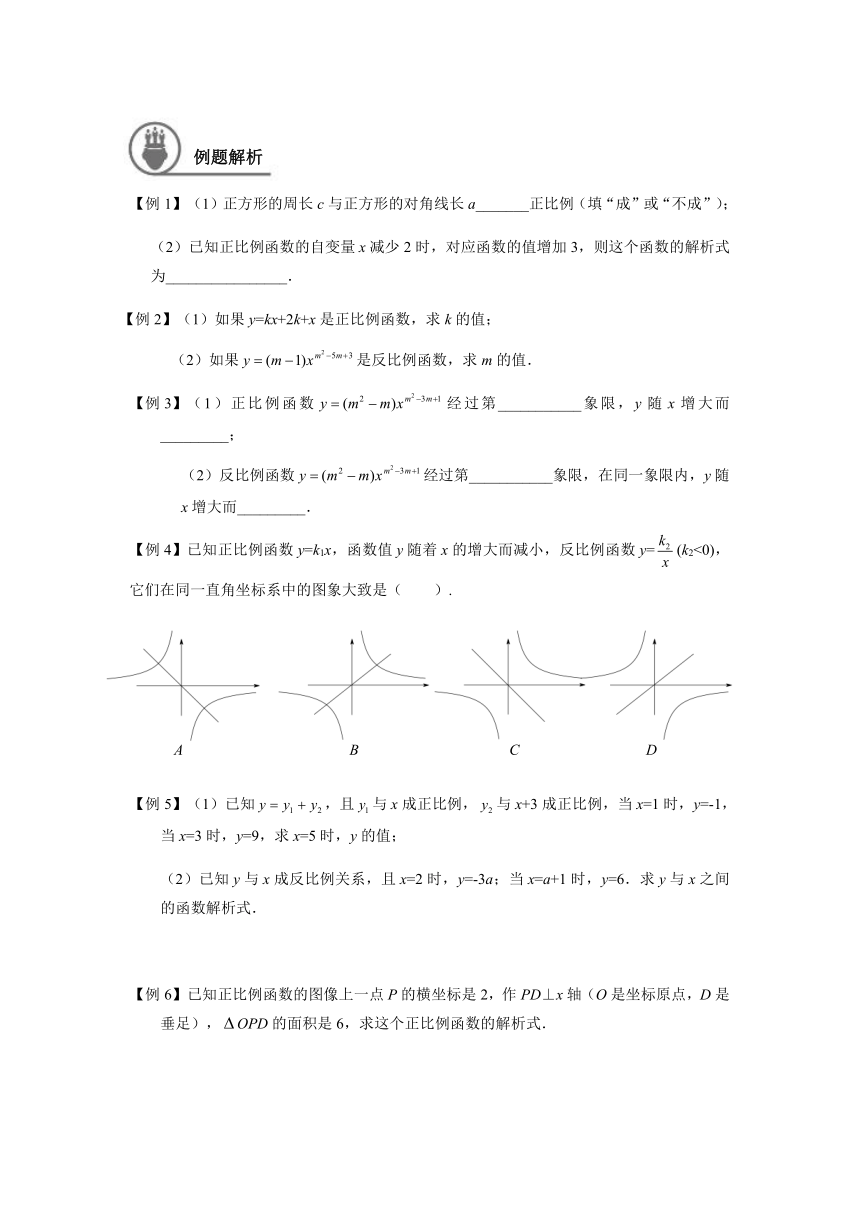
已知正比例函数y=k1x,函数值y随着x的增大而减小,反比例函数y=(k2<0),它们在同一直角坐标系中的图象大致是( ).
(1)已知,且与x成正比例,与x+3成正比例,当x=1时,y=-1,当x=3时,y=9,求x=5时,y的值;
(2)已知y与x成反比例关系,且x=2时,y=-3a;当x=a+1时,y=6.求y与x之间的函数解析式.
已知正比例函数的图像上一点P的横坐标是2,作PD⊥x轴(O是坐标原点,D是垂足),OPD的面积是6,求这个正比例函数的解析式.
已知如图,点A,B是反比例函数y=图像上的点,分别经过A,B两点向x轴、y轴做垂线段,若_________(指的是空白矩形的面积).
已知A(0,4)、B(6,4)、C(6,0)三点,经过原点的一条直线把矩形OABC的面积分成1:2两部分,求这条直线的函数解析式.
在平面直角坐标系中,O为坐标原点,点A的坐标为(1,0),在直线上取一点P,使得OAP是等腰三角形,求所有满足条件的点P的坐标.
已知如图,矩形OABC的顶点B(m,2)在正比例函数的图像上,点A在x轴上,点C在y轴上,反比例函数的图像过BC边上点M,与AB边交于点N,且BM=3CM,求此反比例函数的解析式及点N的坐标.
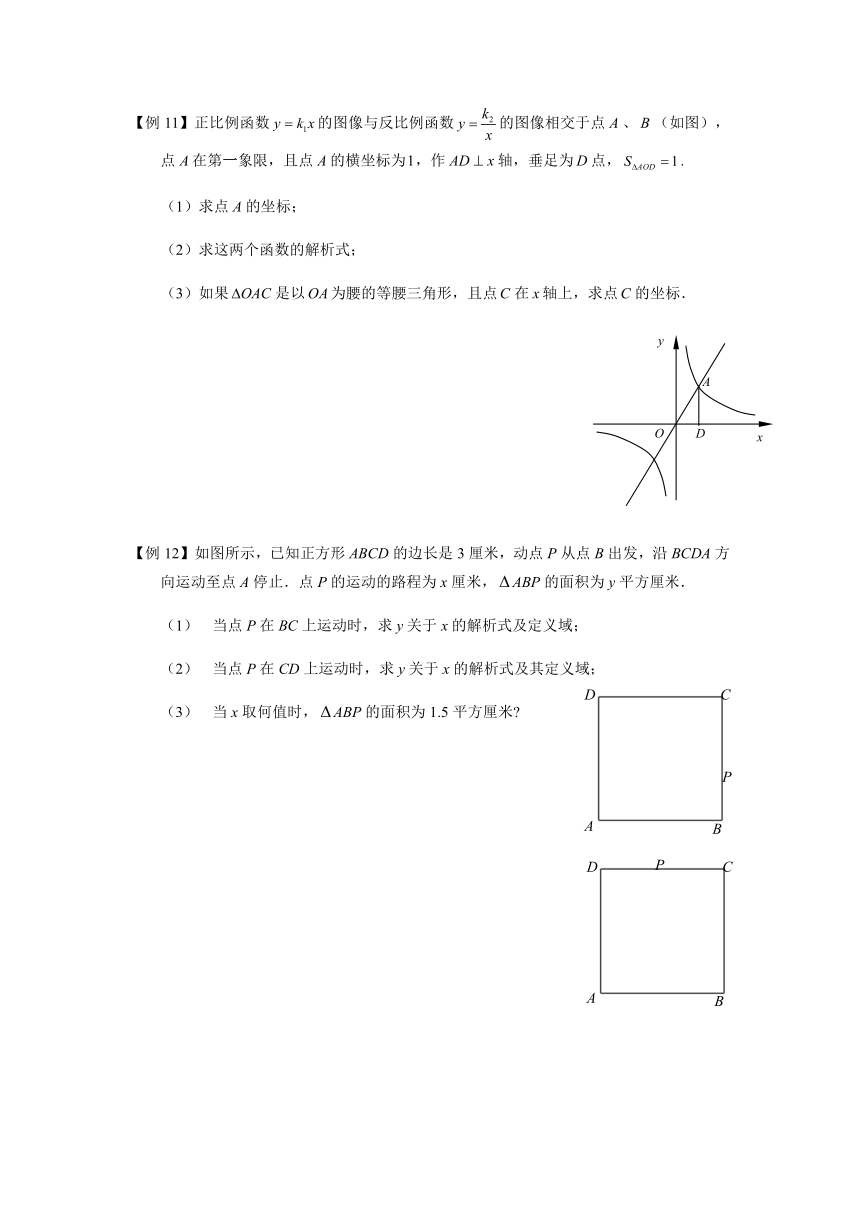
正比例函数的图像与反比例函数的图像相交于点、(如图),点在第一象限,且点的横坐标为,作轴,垂足为点,.
(1)求点的坐标;
(2)求这两个函数的解析式;
(3)如果是以为腰的等腰三角形,且点在轴上,求点的坐标.
如图所示,已知正方形ABCD的边长是3厘米,动点P从点B出发,沿BCDA方向运动至点A停止.点P的运动的路程为x厘米,ABP的面积为y平方厘米.
当点P在BC上运动时,求y关于x的解析式及定义域;
当点P在CD上运动时,求y关于x的解析式及其定义域;
当x取何值时,ABP的面积为1.5平方厘米?
1.函数的概念和图像及性质
(1)定义:解析式形如的函数叫做一次函数.
(2)一次函数的图象满足:
①形状是一条直线;②始终经过(0,b)和(,0)两点;
(3)定义:直线与y轴的交点坐标是,截距是b;
(4)一次函数,当时,函数值y随自变量x的值增大而增大;当 时,函数值y随自变量x的值增大而减小.
2.函数的应用
(1)实际问题;
(2)数形结合类.
(1)已知一次函数,当x=-3时,y=1;当x=2时,y=-6,求这个一次函数的解析式;
(2)已知一次函数y=f(x),且f(-1)=-3,f(1)=1,求函数f(x)的解析式.
(1)若一次函数y=k(1-x)+3的图像在y轴上的截距是-5,求这个函数解析式;
(2)若一次函数的图像经过原点,求k的值.
(1)若直线y=kx+b与直线y=-2x+4无交点,且直线y=kx+b与x轴的交点是
(3,0),求此函数解析式;
(2)已知一次函数的图像经过点(1,-2)、(-2,1).求这个一次函数的解析式.
(1)若把函数的图像向下平移4个单位,再向右平移2个单位,求平移
后的函数解析式;
(2)若一次函数的图像向下平移4个单位,再向右平移2个单位得到的函数解析式是,求平移前的函数解析式.
已知直线y=kx+4经过点P(1,m),且平行于直线y=-2x+1,它与x轴相交于点A,求OPA的面积.
已知一次函数的自变量的取值范围是,相应的函数值的范围是,求这个函数的解析式.
已知直线l过点(-2,4),且与两坐标轴围成一个等腰三角形,
(1)求这个一次函数的解析式;
(2)所得三角形的周长及面积.
某中学初二年级准备购买10只米奇品牌的笔袋,每只笔袋配x(x≥3)支水笔作为奖品.已知A、B两家超市都有这个牌子的笔袋和水笔出售,而且每只笔袋的标价都为20元,每只水笔的标价都为1元,现两家超市正在促销,A超市所有商品均打九折销售,而B超市买1只笔袋送3支水笔,若仅考虑购买笔袋和水笔的费用,请解答下列的问题:
如果只在某一家超市购买所需笔袋和水笔,那么去哪家超市购买更合算?
当x=12时,请设计最省钱的购买方案.
若直线过与的交点A,与y轴于B,交x轴于C,若,求直线y=的解析式.
已知反比例函数和一次函数,其中一次函数的图像经过点
(k,5).
试求反比例函数的解析式;
若点A在第一象限,且同时在上述两个函数的图像上,求点A的坐标.
【难度】★★
【答案】(1);(2).
【解析】(1)∵一次函数经过点(k,5),∴,∴点坐标为(3,5),
又因为这个点在反比例函数上,所以反比例函数的解析式为;
令,解得:,,代入可得:,,
∵点A在第一象限,∴.
【总结】考察反比例解析式的求法和交点坐标的求法.
如图,一次函数的图像与x轴、y轴分别交于点A、B两点,且与反比例函数的图像在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
求点A、B、D的坐标;
求一次函数和反比例函数的解析式.
【难度】★★
【答案】(1);
(2),.
【解析】(1)∵OA=OB=OD=1,∴;
(2)∵一次函数的图像与x轴、y轴分别交于点A、B两点,
∴;
∵C在上,∴.
∵在上, ∴.
【总结】考察反比例函数和一次函数的解析式求法.
如图,一次函数的图像与与反比例函数的图像交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,
求:(1)一次函数的解析式;(2)AOB的面积.
【难度】★★
【答案】(1);(2)6.
【解析】(1)∵点A的横坐标和点B的纵坐标都是-2,
且两点都在反比例函数的图像上,
∴,
∵两点都在一次函数上,
∴, ∴,
∴一次函数解析式为:;
∵一次函数与轴的交点为,
∴.
【总结】考察反比例函数和一次函数解析式的求法及三角形面积的求法.
已知点A(m,2m)(其中m>0)在双曲线上,直线y=kx+b过点A,并且与坐标轴正方向所围成的三角形的面积是18,求直线的解析式.
【难度】★★
【答案】或.
【解析】∵点A(m,2m)(其中m>0)在双曲线上,
∴,∴或,∵,∴,∴
∵直线y=kx+b过点A,∴
∵直线y=kx+b与坐标轴正方向所围成的三角形的面积是18,
∴,解得:或
当时,,直线的解析式为;
当时,,直线的解析式为.
【总结】考察反比例函数、一次函数解析式的求法和面积问题的处理方法.
已知一次函数与反比例函数的图像交于点P(-3,2)、Q(2,-3).
求这两个函数的函数解析式;
在给定的直角坐标系中,画出这两个函数的大致图像;
当x为何值时,一次函数的值大于反比例函数的值?当x为何值时,一次函数的值小于反比例函数的值?
【难度】★★
【答案】见解析.
【解析】(1)反比例的函数解析式为
设一次函数的解析式为,
则可得:,
解得:,
所以一次函数解析式为;
(2)如右图;
当或时,一次函数的值大于反比例函数的值;
当或时,一次函数的值小于反比例函数的值.
【总结】考察反比例函数、一次函数的解析式的求法和函数性质的分析.
已知一次函数;
(1)求证:无论取何实数,函数的图像恒过一定点;
(2)当在内变化时,在内变化,求的值.
【难度】★★★
【答案】(1)见解析;(2).
【解析】(1),当,即时,,
∴无论取何实数,函数的图像恒过一定点;
当时,, 解得:;
当时,, ∴解不等式后不存在这样的m值,
所以.
【总结】考察解析式图像恒过一定点的条件和一次函数的增减性的运用.
如图所示,双曲线在第一象限的一支上有一点C(1,5),过点C的直线与x轴交于点A(a,0)、与y轴交于点B.
求点A的横坐标a与k之间的函数关系式;
当该直线与双曲线在第一象限的另一交点D的横坐标是9时,求△COD的面积.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵点C(1,5),A(a,0)在上,
∴,,
∴,
∵D的横坐标是9,且双曲线,
∴.
分别过点C作CE⊥轴,过点D作DF⊥轴,
则
.
【总结】考察反比例函数与一次函数解析式的求法,图中由于△OCE和△OFD的面积相等,则△OCD的面积与梯形CEFD的面积相等.
(1)y与x成正比例,且x=4时,y=-4,那么y与x之间的函数关系式为__________;
(2)y+1与z成正比例,比例系数为2,z与x-1成正比例,当x=-1时,y=7,那么y 与x的函数关系式为____________
【难度】★
【答案】(1);(2).
【解析】(1)由题意可知,函数关系式为:;
∵y+1与z成正比例,比例系数为2,
∴;
∵z与x-1成正比例,∴设,
∴,
∵当x=-1时,y=7,∴,
∴.
【总结】考察正比例的定义.
已知y是x的函数,y与x-1成正比例,如果这个函数的图象经过点(α,α)(α≠0),
则它的图象大致是( )
【难度】★
【答案】B
【解析】∵y与x-1成正比例,∴,则此函数为一次函数,且不经过原点,
则选B.
【总结】考察正比例的定义和函数图像的画法.
已知y-3与x成正比例,且x=2时,y=7.
写出y与x的函数关系式;
计算x=4时y的值;
计算y=4时x的值.
【难度】★
【答案】(1);(2)11;(3).
【解析】(1)设, ∵x=2时,y=7,∴, ∴;
当时,;
当时,.
【总结】考察正比例的定义,及根据其中一个变量的值求另一个变量的值.
已知一次函数的图像交轴于A(,0),交正比例函数的图像于点B,且点B 在第三象限,它的横坐标为,的面积为6,求正比例函数和一次函数的解析 式.
【难度】★★
【答案】正比例函数:;一次函数:.
【解析】∵的面积为6,
∴, ∴
∵点B在第三象限,它的横坐标为,
∴
则正比例函数的解析式为.
设一次函数的解析式为
则,∴,
∴一次函数的解析式为
【总结】考察一次函数的解析式的求法和面积的处理方法.
已知函数y=的图象和两条直线y=x、y=2x在第一象限内分别交于P1和P2两点, 过点P1分别作x轴、y轴的垂线P1Q1、P1R1,垂足分别为Q1、R1;过点P2分别作x轴、 y轴的垂线P2Q2、P2R2,垂足分别为Q2、R2,求矩形OQ1P1R1和OQ2P2R2的周长并比 较它们的大小.
【难度】★★
【答案】,
,
.
【解析】∵是函数和在第一象限的交点,
∴,∴,∴
∵是函数和在第一象限的交点
∴,∴,∴
∴,
∵,∴.
【总结】考察函数交点的求法及几何图形的周长及大小比较.
如图,正方形的面积为9,点O为坐标原点,点B在函数 的图象上,点P(m,n)是函数的图象上任意一点,边点P分别作 x轴、y轴的垂线.垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面 积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(1)B点的坐标是___________;=__________;
(2)时,P的坐标是___________;
(3)求出S关于m的函数关系式.
【难度】★★
【答案】(1),;(2)或;
(3)或.
【解析】(1)由正方形的面积为9,得,
∴反比例函数的解析式为:;
当点P在点B右侧时,
∵, ∴, ∴的纵坐标为.
∵点在函数的图像上,∴;
当点P在点B左侧时,同理可得P点的坐标为,
综上,点P的坐标为或;
∵P(m,n)是函数上, ∴设.
当点在点的右侧时,, ∴;
当点在点的左侧时,,∴.
【总结】考察反比例函数的解析式的求法和面积的处理方法,注意分类讨论.
为了更好的治理某个湖水水质,保护环境,治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:
A型 B型
价格(万元/台) a b
处理污水量(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买 3台B型设备少6万元.
求a、b的值;
经预算:治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
在(2)问的条件下,若每月要求处理该湖泊的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
【难度】★★
【答案】见解析.
【解析】(1)由题意,可得:, 解得:;
设购买A型设备台,则购买B型设备台,
由题意,可得:, 解得:.
∵取自然数, ∴为0,1,2.
∴该公式有三种购买方案:①购买10台B型设备;②购买1台A型设备,9台B型设
备;③购买2台A型设备,8台B型设备.
由题意,可得:,解得:, ∴的值为1或2.
当为1时,共需花费,
当为2时,共需花费,
∴最省钱的购买方案是购买1台A型设备,9台B型设备.
【总结】考察一次函数在实际问题中的应用,此题是有关最优方案的问题,解题时注意进行讨论.
已知在直角坐标平面内,直线AB经过原点O和点(1,-2),点P是直线AB 上一点,若过点P向y轴作垂直,垂足为M,且OPM的面积为9,求点P的坐标.
【难度】★★★
【答案】或.
【解析】∵直线AB经过原点O和点(1,-2),
∴直线AB为正比例函数,解析式为.
设
∵△OPM的面积为, ∴,解得:
∴或.
【总结】考察面积的处理方法,注意点坐标和线段长的转换中正负号或绝对值的添法.
如图,在梯形ΑBCD中,ΑB=CD=5,ΑD=7,BC=13,E为ΑD上一定点,ΑE=4, 动点P从D出发沿着DC向C点移动,设点P移动的距离为x,ΑPE的面积为y,
求y与x的函数解析式,并画出图象.
【难度】★★★
【答案】,图像略.
【解析】分别过点A、D作AM⊥BC,DN⊥BC,垂足分别为M、N.
可得:,.
∵,, ∴,即,
∴, ∵,即,∴, ∴.
【总结】考察面积中同底等高的处理方法.
在平面直角坐标系中,函数y=2x+12的图像分别交x轴、y轴于A、B两点.过 点A的直线交y轴正半轴于点M,且点M为线段OB的中点.
求直线AM的解析式;
试在直线AM上找一点P,使得,求出点P的坐标.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵函数y=2x+12的图像分别交x轴、y轴于A、B两点,
∴,.
∵点M为线段OB的中点,
∴.
∴利用待定系数法,可得直线AM的解析式为:;
∵, ∴,∴,
即O到直线AB的距离和P到直线AB的距离相等,
∴
∴直线OP的解析式为
∵点P在直线AM上,
∴令,解得:.
∴点P的坐标为.
【总结】考察一次函数解析式的求法和同底等高的两个三角形面积相等的运用.
如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的
坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;
(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;
(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时t的值?
【难度】★★★
【答案】见解析.
【解析】(1)由题意可知,点B坐标为,
∴,
由,得:,此时P在CB上;
∵, ∴,
∴;
经分析,可知点P只能在AB或OC上.
当点P在AB边上时,设点P的坐标为,
由,得:,解得:,此时,
当点P在OC上时,设点P的坐标为,
由得:,解得:,
此时.
∴在7秒或者秒时,线段PD将梯形COAB的面积分成1:3的两部分.
【总结】本题综合性较强,主要考察勾股定理和直角梯形的性质的综合运用,注意认真分析题意.
(1)若是关于x的一次函数,则m的值?
(2)可能是正比例函数吗?可能是反比例函数吗?如果是,求出m 的值.
【难度】★
【答案】见解析.
【解析】(1)由或,∴;
当函数为正比例函数时,且,所以不可能为正比例函数;
当函数为反比例函数时,且,所以不可能是反比例函数.
【总结】考察正比例函数、反比例函数的定义.
在下列函数解析式中,属于一次函数的是( )
(1) (2)
(3) (4)
A.(1) B.(1)(3) C.(1)(2)(3) D.全部都是
【难度】★
【答案】C
【解析】形如(,为常数).
【总结】考察一次函数的定义.
如果一次函数的图像经过一、二、四象限,那么的大致图像为( ).
【难度】★
【答案】B
【解析】∵一次函数的图像经过一、二、四象限,∴,
∴经过一、三、四象限.
【总结】考察一次函数的图像及性质.
已知函数y=,点P为图象上的任意一点,过P作PA⊥x轴A,PB⊥y轴于B,则APB的面积为_______________.
【难度】★
【答案】4
【解析】矩形OAPB的面积为8,△APB的面积矩形的一半.
【总结】考察反比例函数的面积问题的处理方法.
已知y1与成正比例,y2与3x成反比例,,当x=1时,y=4,当x=-1时,y=0,求y和x的函数关系式.
【难度】★
【答案】.
【解析】∵y1与成正比例,y2与3x成反比例,
∴设,, ∴
∵当x=1时,y=4;当x=-1时,y=0, ∴, 解得:,
∴y和x的函数关系式为:.
【总结】考察正比例和反比例的概念,并且考查了复合函数解析式的确定.
若A(a1,b1),B(a2,b2)是反比例函数图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
A.b1<b2 B.b1 =b2 C.b1>b2 D.大小不确定
【难度】★★
【答案】D
【解析】反比例函数在每个象限里面随着的增大而增大.因为A、B两点不确定
在哪个象限,所以不确定纵坐标的大小关系.
【总结】考察反比例函数的增减性,注意要分象限.
如图,已知点A是一次函数y=x的图象与反比例函数的图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么AOB的面积为( )
A.2 B. C. D.
【难度】★★
【答案】C
【解析】∵点A是一次函数y=x的图象与反比例函数的图象在
第一象限内的交点,∴,∴,∴,∴
∵,∴, ∴, 故选C.
【总结】考察函数交点的求法,从而求出三角形的面积.
为了鼓励小强勤做家务,培养他的劳动意识,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费为y元,则y(元)和x(小时)之间的函数图像如图所示.
(1)根据图像,请你写出小强每月的基本生活费为多少元;父母是如何奖励小强家务劳动的?
(2)写出当0≤x≤20时,相对应的y与x之间的函数关系式;
(3)若小强5月份希望有250元费用,则小强4月份需做家务多少时间?
【难度】★★
【答案】见解析.
【解析】(1)小强每月的基本生活费为150元;如果小强每月家务劳动时间不超过20小时,
每小时奖励2.5元;如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5
元奖励,超过部分按每小时4元奖励.
设直线方程为,
∵当时,图像经过
∴, 解得:,
∴y与x之间的函数关系式为:;
(3)当时,图像经过点,
∴, 解得:, ∴
则有题意可得:, 解得:
∴当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
【总结】考察一次函数在实际问题中的运用.
现有一个种植总面积为540m2的矩形塑料温棚,分垄间隔种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物不低于10垄,又不超过14垄(垄数为整数),它们的占地面积、产量、利润分别如下:
占地面积(m2/垄) 产量(千克/垄) 利润(元/千克)
西红柿 30 160 1.1
草莓 15 50 1.6
若草莓共种植了x垄,通过计算说明共有几种种植方案?分别是哪几种?
在几种种植方案中.哪种方案获利最大?最大的利润是多少?
【难度】★★★
【答案】见解析
【解析】(1)根据题意西红柿种了垄,则,解得:
∵,且是正整数,∴,
∴共有三种种植方案:①草莓种植12垄,西红柿种植12垄;②草莓种植13垄,西红
柿种植11垄;③草莓种植14垄,西红柿种植10垄;
设种植草莓和西红柿共可获得利润元,
则
∵随着的增大而减小,∴取最小值12时,有最大值为3072元.
即草莓种植12垄,西红柿种植12垄时,有最大利润为3072元.
【总结】考察一元一次不等式与一次函数的综合应用.
在反比例函数的图像上有不重合的两点A、B,且A点的纵坐标是2,B点的横坐标是2,BB'和AA'都垂直于x轴,B',A'为垂足.(1)求A点的横坐标;
(2)求的值;(3)求的值.
【难度】★★★
【答案】(1)4;(2)4;(3)6.
【解析】(1)∵A、B两点都在反比例函数的图像上,且A点的纵坐标是2,
∴A点的横坐标是4;
(2)由题意,可得:;
(3)
.
在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线平行.
(1)求:直线l的函数解析式及点B的坐标;
(2)如直线l上有一点M(a,-6),过点M作x轴的垂线,交直线于点N,在线段MN上求一点P,使PAB是直角三角形,请求出点P的坐标.
【难度】★★★
【答案】(1),;(2)或.
【解析】(1)∵直线l与直线平行,
∴设直线l的解析式为,
∵直线l经过点A(2,-3),
∴,
∴直线l的解析式为,
∴点B的坐标为;
∵直线l上有一点M(a,-6), ∴,
则可设,
∵, ∴的取值范围是.
当AB为斜边时,
∴,
解得:,
∴点P的坐标为;
当PB为斜边时,
∴,
解得:, ∴点P的坐标为;
当PA为斜边时,,
∴,解得:,舍去
综上所述,点P的坐标为或.
【总结】考察一次函数的解析式求法和直角三角形分类讨论,本题综合性较强,注意认真分析.
初二数学寒假班(学生版)
教师
日期
学生
课程编号
课型 新课
课题 函数的复习
教学目标
熟悉正反比例及一次函数的概念和性质 能利用函数的性质解决相应的问题即求角或者边之间的关系
能够运动数形结合的思想解决几何背景下的函数问题.
教学重点
熟练的运用函数的性质
运用一次函数模型解决实际问题.
运用一次函数的图像与性质求解初步几何问题.
教学安排
版块 时长
1 正反比例函数 20min
2 一次函数 30min
3 函数的综合 50min
4 作业 20min
正比例函数:y=kx(k≠0);图像是一条直线,与坐标轴仅有一个交点;k>0时,随着x
的逐渐增大,函数值y的值越来越大;k<0时,随着x的逐渐增大,函数值y的值越来
越小.
反比例函数:(k≠0),图像是双曲线,与坐标轴无交点;k>0时,在每一象限内,
随着x的逐渐增大,函数值y的值越来越小;k<0时,在每一象限内,随着x的逐渐增
大,函数值y的值越来越大.
(1)正方形的周长c与正方形的对角线长a_______正比例(填“成”或“不成”);
(2)已知正比例函数的自变量x减少2时,对应函数的值增加3,则这个函数的解析式为________________.
【难度】★
【答案】(1)成;(2).
【解析】(1)正方形的对角线长为,则正方形的边长为,则,
为一定值,所以成正比例.
设,则由题意,可得:,解得:,
从而可得这个函数的解析式为.
【总结】考察正比例的定义和正比例函数解析式的求法.
(1)如果y=kx+2k+x是正比例函数,求k的值;
(2)如果是反比例函数,求m的值.
【难度】★
【答案】(1)0;(2)4.
【解析】(1)因为是正比例函数,所以,解得:;
(2)因为函数是反比例函数,
所以可得, ,∴.
【总结】考察正比例函数和反比例函数的定义,注意比例系数要不为零.
(1)正比例函数经过第___________象限,y随x增大而_________;
(2)反比例函数经过第___________象限,在同一象限内,y随x增大而_________.
【难度】★
【答案】(1)一、三,增大;(2)一、三,减小.
【解析】(1)因为是正比例函数,所以可得,解得:,
∴函数解析式为,图像过一、三象限,y随x的增大而增大;
因为是反比例函数,所以可得,解得:,
∴函数解析式为,图像过一、三象限,y随x的增大而减小.
【总结】考察正、反比例函数的概念和性质,注意比例系数不为零.
已知正比例函数y=k1x,函数值y随着x的增大而减小,反比例函数y=(k2<0),它们在同一直角坐标系中的图象大致是( ).
【难度】★
【答案】A
【解析】由题意可知:正比例函数在二、四象限;反比例函数在二、四象限,故选A.
【总结】考察正、反比例函数的图像及性质.
(1)已知,且与x成正比例,与x+3成正比例,当x=1时,y=-1,当x=3时,y=9,求x=5时,y的值;
(2)已知y与x成反比例关系,且x=2时,y=-3a;当x=a+1时,y=6.求y与x之间的函数解析式.
【难度】★★
【答案】(1)19;(2).
【解析】(1)设,,则,
由题意可得:,解得:,∴
∴当时,;
设,则可得:,∴, ∴.
【总结】本题一反面考察了复合函数解析式的确定,另一方面考查了反比例函数的概念.
已知正比例函数的图像上一点P的横坐标是2,作PD⊥x轴(O是坐标原点,D是垂足),OPD的面积是6,求这个正比例函数的解析式.
【难度】★★
【答案】或.
【解析】由题意可得:,,则,∴或
则正比例函数的解析式为或
【总结】考察正比例函数解析式的求法,注意长度转成点坐标需要注意正负.
已知如图,点A,B是反比例函数y=图像上的点,分别经过A,B两点向x轴、y轴做垂线段,若_________(指的是空白矩形的面积).
【难度】★★
【答案】4
【解析】∵,,,
∴,,∴.
【总结】考察反比例函数的面积问题.过反比例函数
上任意一点作x轴、y轴的垂线,构成的矩形的面积为.
已知A(0,4)、B(6,4)、C(6,0)三点,经过原点的一条直线把矩形OABC的面积分成1:2两部分,求这条直线的函数解析式.
【难度】★★
【答案】或.
【解析】矩形OABC的面积为24,因为直线将矩形分成1:2两部分,则其中较小部分的面
积为8.当经过原点的一条直线与AB相交时,其交点为D,则,则,
∴,此时正比例函数解析式为;
当经过原点的一条直线与CB相交时,其交点为E,则,则,
∴,此时正比例函数解析式为.
【总结】考察面积的处理方法和正比例函数解析式的求法,注意分类讨论.
在平面直角坐标系中,O为坐标原点,点A的坐标为(1,0),在直线上取一点P,使得OAP是等腰三角形,求所有满足条件的点P的坐标.
【难度】★★★
【答案】或或或 .
【解析】当时,P点在OA的线段垂直平分线上,则P点的横坐标为,
代入函数解析式可得纵坐标为,∴;当时,设,
则,∴,∴或;
当时,设, 则,∴,
∴或,其中与原点重合舍去.
综上所述,满足题意的点坐标为或或或.
已知如图,矩形OABC的顶点B(m,2)在正比例函数的图像上,点A在x轴上,点C在y轴上,反比例函数的图像过BC边上点M,与AB边交于点N,且BM=3CM,求此反比例函数的解析式及点N的坐标.
【难度】★★★
【答案】,.
【解析】∵B(m,2)在正比例函数的图像上,∴.
∵BM=3CM,∴,∴,
∴反比例函数的解析式为,∴.
【总结】考察反比例函数的解析式的求法和点坐标的求法.
正比例函数的图像与反比例函数的图像相交于点、(如图),点在第一象限,且点的横坐标为,作轴,垂足为点,.
(1)求点的坐标;
(2)求这两个函数的解析式;
(3)如果是以为腰的等腰三角形,且点在轴上,求点的坐标.
【难度】★★★
【答案】见解析.
【解析】(1)由题可知,点A坐标为:;
(2)反比例函数解析式为;正比例函数解析式为;
(3)当时,,则或,
当时,由等腰三角形三线合一性质可得:,∴
综上所述:或或.
【总结】考察正反比例函数解析式的求法和等腰三角形的分类讨论.
如图所示,已知正方形ABCD的边长是3厘米,动点P从点B出发,沿BCDA方向运动至点A停止.点P的运动的路程为x厘米,ABP的面积为y平方厘米.
当点P在BC上运动时,求y关于x的解析式及定义域;
当点P在CD上运动时,求y关于x的解析式及其定义域;
当x取何值时,ABP的面积为1.5平方厘米?
【难度】★★★ 【答案】见解析.
【解析】(1)当点P在BC上运动时,
∴;
当点P在CD上运动时,,
∴;
,∴
当P在BC边上时,;当P在DA边上时,.
1.函数的概念和图像及性质
(1)定义:解析式形如的函数叫做一次函数.
(2)一次函数的图象满足:
①形状是一条直线;②始终经过(0,b)和(,0)两点;
(3)定义:直线与y轴的交点坐标是,截距是b;
(4)一次函数,当时,函数值y随自变量x的值增大而增大;当 时,函数值y随自变量x的值增大而减小.
2.函数的应用
(1)实际问题;
(2)数形结合类.
(1)已知一次函数,当x=-3时,y=1;当x=2时,y=-6,求这个一次函数的解析式;
(2)已知一次函数y=f(x),且f(-1)=-3,f(1)=1,求函数f(x)的解析式.
【难度】★
【答案】(1);(2).
【解析】(1)由题意可得:,解得:,
则一次函数解析式为;
设,
由题意可得:, 解得:,
则一次函数解析式为.
【总结】考察利用待定系数法求一次函数解析式的求解析式.
(1)若一次函数y=k(1-x)+3的图像在y轴上的截距是-5,求这个函数解析式;
(2)若一次函数的图像经过原点,求k的值.
【难度】★
【答案】(1);(2).
【解析】(1)若一次函数y=k(1-x)+3的截距为,则,
所以这个函数的解析式为
∵图像过原点,
∴且, ∴
【总结】考察一次函数的截距等概念.
(1)若直线y=kx+b与直线y=-2x+4无交点,且直线y=kx+b与x轴的交点是
(3,0),求此函数解析式;
(2)已知一次函数的图像经过点(1,-2)、(-2,1).求这个一次函数的解析式.
【难度】★
【答案】(1);(2).
【解析】(1)∵直线y=kx+b与直线y=-2x+4无交点,
∴直线y=kx+b与直线y=-2x+4平行,∴,故解析式为,
∵直线y=kx+b与x轴的交点是(3,0),∴,
∴函数解析式为;
(2)设,
由题意可得:,解得:,则一次函数解析式为.
【总结】考察一次函数解析式的求法,注意两直线的位置关系与k和b的关系.
(1)若把函数的图像向下平移4个单位,再向右平移2个单位,求平移
后的函数解析式;
(2)若一次函数的图像向下平移4个单位,再向右平移2个单位得到的函数解析式是,求平移前的函数解析式.
【难度】★★
【答案】(1);(2).
【解析】(1)利用平移规则,可知平移后的函数解析式为:;
利用平移规则,可知平移后的函数解析式为:.
已知直线y=kx+4经过点P(1,m),且平行于直线y=-2x+1,它与x轴相交于点A,求OPA的面积.
【难度】★★
【答案】2.
【解析】∵直线y=kx+4平行于直线y=-2x+1, ∴, 则,
则它与x轴相交于点.
∵直线经过点P(1,m),∴, ∴.
∴△POA的面积为:.
【总结】考察一次函数的图像性质及与三角形面积的结合.
已知一次函数的自变量的取值范围是,相应的函数值的范围是,求这个函数的解析式.
【难度】★★
【答案】或.
【解析】当时,则有, 解得:,
这个函数解析式为;
当时,则有,解得:,
这个函数解析式为.
【总结】考察一次函数的性质,注意此类题要有两种情况的分类讨论.
已知直线l过点(-2,4),且与两坐标轴围成一个等腰三角形,
(1)求这个一次函数的解析式;
(2)所得三角形的周长及面积.
【难度】★★
【答案】见解析.
【解析】设一次函数的解析式为,
∵函数图像与两坐标轴围成一个等腰三角形, ∴,则
当时,一次函数为,直线l过点(-2,4),∴,∴
与坐标轴的交点为,,此时周长为,面积为18;
当时,一次函数为,直线l过点(-2,4),∴,∴,
与坐标轴的交点为,,此时周长为,面积为2.
【总结】考察一次函数的性质,注意线段长与点坐标之间的转换.
某中学初二年级准备购买10只米奇品牌的笔袋,每只笔袋配x(x≥3)支水笔作为奖品.已知A、B两家超市都有这个牌子的笔袋和水笔出售,而且每只笔袋的标价都为20元,每只水笔的标价都为1元,现两家超市正在促销,A超市所有商品均打九折销售,而B超市买1只笔袋送3支水笔,若仅考虑购买笔袋和水笔的费用,请解答下列的问题:
如果只在某一家超市购买所需笔袋和水笔,那么去哪家超市购买更合算?
当x=12时,请设计最省钱的购买方案.
【难度】★★★
【答案】见解析.
【解析】(1)A家超市共付(x≥3);
B家超市共付(x≥3);
当时,则; 当时,则;
当时,则;
所以每只笔袋配10只笔时,A、B两家超市都一样;
每只笔袋配超过10只笔时,选A家超市更合算;
每只笔袋配超过10只但是不少于3只笔时,选B家超市更合算;
(2)当x=12时,即要10支笔袋,配120支笔.
设总费用为b,在A超市买a只笔袋,在B超市买(10-a)只,送了3(10-a)支笔,
则
故当时,总费用最少,为281元,
因此在B超市买10只笔袋,在A超市买90支水笔是最省钱的购买方案.
【总结】考察一次函数的应用.
若直线过与的交点A,与y轴于B,交x轴于C,若,求直线y=的解析式.
【难度】★★★
【答案】.
【解析】∵与的交点A为,与y轴交于点B,
交x轴于点C
又∵直线过A为, ∴,
∴过A作AE⊥x轴,垂足为E,
当时,
,
解得:(舍去)
当时,设直线AE与BC相交于F
∴
∵, ∴,
∴直线解析式为.
【总结】考察面积问题的处理方法,注意分类讨论.
已知反比例函数和一次函数,其中一次函数的图像经过点
(k,5).
试求反比例函数的解析式;
若点A在第一象限,且同时在上述两个函数的图像上,求点A的坐标.
【难度】★★
【答案】(1);(2).
【解析】(1)∵一次函数经过点(k,5),∴,∴点坐标为(3,5),
又因为这个点在反比例函数上,所以反比例函数的解析式为;
令,解得:,,代入可得:,,
∵点A在第一象限,∴.
【总结】考察反比例解析式的求法和交点坐标的求法.
如图,一次函数的图像与x轴、y轴分别交于点A、B两点,且与反比例函数的图像在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
求点A、B、D的坐标;
求一次函数和反比例函数的解析式.
【难度】★★
【答案】(1);
(2),.
【解析】(1)∵OA=OB=OD=1,∴;
(2)∵一次函数的图像与x轴、y轴分别交于点A、B两点,
∴;
∵C在上,∴.
∵在上, ∴.
【总结】考察反比例函数和一次函数的解析式求法.
如图,一次函数的图像与与反比例函数的图像交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,
求:(1)一次函数的解析式;(2)AOB的面积.
【难度】★★
【答案】(1);(2)6.
【解析】(1)∵点A的横坐标和点B的纵坐标都是-2,
且两点都在反比例函数的图像上,
∴,
∵两点都在一次函数上,
∴, ∴,
∴一次函数解析式为:;
∵一次函数与轴的交点为,
∴.
【总结】考察反比例函数和一次函数解析式的求法及三角形面积的求法.
已知点A(m,2m)(其中m>0)在双曲线上,直线y=kx+b过点A,并且与坐标轴正方向所围成的三角形的面积是18,求直线的解析式.
【难度】★★
【答案】或.
【解析】∵点A(m,2m)(其中m>0)在双曲线上,
∴,∴或,∵,∴,∴
∵直线y=kx+b过点A,∴
∵直线y=kx+b与坐标轴正方向所围成的三角形的面积是18,
∴,解得:或
当时,,直线的解析式为;
当时,,直线的解析式为.
【总结】考察反比例函数、一次函数解析式的求法和面积问题的处理方法.
已知一次函数与反比例函数的图像交于点P(-3,2)、Q(2,-3).
求这两个函数的函数解析式;
在给定的直角坐标系中,画出这两个函数的大致图像;
当x为何值时,一次函数的值大于反比例函数的值?当x为何值时,一次函数的值小于反比例函数的值?
【难度】★★
【答案】见解析.
【解析】(1)反比例的函数解析式为
设一次函数的解析式为,
则可得:,
解得:,
所以一次函数解析式为;
(2)如右图;
当或时,一次函数的值大于反比例函数的值;
当或时,一次函数的值小于反比例函数的值.
【总结】考察反比例函数、一次函数的解析式的求法和函数性质的分析.
已知一次函数;
(1)求证:无论取何实数,函数的图像恒过一定点;
(2)当在内变化时,在内变化,求的值.
【难度】★★★
【答案】(1)见解析;(2).
【解析】(1),当,即时,,
∴无论取何实数,函数的图像恒过一定点;
当时,, 解得:;
当时,, ∴解不等式后不存在这样的m值,
所以.
【总结】考察解析式图像恒过一定点的条件和一次函数的增减性的运用.
如图所示,双曲线在第一象限的一支上有一点C(1,5),过点C的直线与x轴交于点A(a,0)、与y轴交于点B.
求点A的横坐标a与k之间的函数关系式;
当该直线与双曲线在第一象限的另一交点D的横坐标是9时,求△COD的面积.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵点C(1,5),A(a,0)在上,
∴,,
∴,
∵D的横坐标是9,且双曲线,
∴.
分别过点C作CE⊥轴,过点D作DF⊥轴,
则
.
【总结】考察反比例函数与一次函数解析式的求法,图中由于△OCE和△OFD的面积相等,则△OCD的面积与梯形CEFD的面积相等.
(1)y与x成正比例,且x=4时,y=-4,那么y与x之间的函数关系式为__________;
(2)y+1与z成正比例,比例系数为2,z与x-1成正比例,当x=-1时,y=7,那么y 与x的函数关系式为____________
【难度】★
【答案】(1);(2).
【解析】(1)由题意可知,函数关系式为:;
∵y+1与z成正比例,比例系数为2,
∴;
∵z与x-1成正比例,∴设,
∴,
∵当x=-1时,y=7,∴,
∴.
【总结】考察正比例的定义.
已知y是x的函数,y与x-1成正比例,如果这个函数的图象经过点(α,α)(α≠0),
则它的图象大致是( )
【难度】★
【答案】B
【解析】∵y与x-1成正比例,∴,则此函数为一次函数,且不经过原点,
则选B.
【总结】考察正比例的定义和函数图像的画法.
已知y-3与x成正比例,且x=2时,y=7.
写出y与x的函数关系式;
计算x=4时y的值;
计算y=4时x的值.
【难度】★
【答案】(1);(2)11;(3).
【解析】(1)设, ∵x=2时,y=7,∴, ∴;
当时,;
当时,.
【总结】考察正比例的定义,及根据其中一个变量的值求另一个变量的值.
已知一次函数的图像交轴于A(,0),交正比例函数的图像于点B,且点B 在第三象限,它的横坐标为,的面积为6,求正比例函数和一次函数的解析 式.
【难度】★★
【答案】正比例函数:;一次函数:.
【解析】∵的面积为6,
∴, ∴
∵点B在第三象限,它的横坐标为,
∴
则正比例函数的解析式为.
设一次函数的解析式为
则,∴,
∴一次函数的解析式为
【总结】考察一次函数的解析式的求法和面积的处理方法.
已知函数y=的图象和两条直线y=x、y=2x在第一象限内分别交于P1和P2两点, 过点P1分别作x轴、y轴的垂线P1Q1、P1R1,垂足分别为Q1、R1;过点P2分别作x轴、 y轴的垂线P2Q2、P2R2,垂足分别为Q2、R2,求矩形OQ1P1R1和OQ2P2R2的周长并比 较它们的大小.
【难度】★★
【答案】,
,
.
【解析】∵是函数和在第一象限的交点,
∴,∴,∴
∵是函数和在第一象限的交点
∴,∴,∴
∴,
∵,∴.
【总结】考察函数交点的求法及几何图形的周长及大小比较.
如图,正方形的面积为9,点O为坐标原点,点B在函数 的图象上,点P(m,n)是函数的图象上任意一点,边点P分别作 x轴、y轴的垂线.垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面 积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(1)B点的坐标是___________;=__________;
(2)时,P的坐标是___________;
(3)求出S关于m的函数关系式.
【难度】★★
【答案】(1),;(2)或;
(3)或.
【解析】(1)由正方形的面积为9,得,
∴反比例函数的解析式为:;
当点P在点B右侧时,
∵, ∴, ∴的纵坐标为.
∵点在函数的图像上,∴;
当点P在点B左侧时,同理可得P点的坐标为,
综上,点P的坐标为或;
∵P(m,n)是函数上, ∴设.
当点在点的右侧时,, ∴;
当点在点的左侧时,,∴.
【总结】考察反比例函数的解析式的求法和面积的处理方法,注意分类讨论.
为了更好的治理某个湖水水质,保护环境,治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:
A型 B型
价格(万元/台) a b
处理污水量(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买 3台B型设备少6万元.
求a、b的值;
经预算:治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
在(2)问的条件下,若每月要求处理该湖泊的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
【难度】★★
【答案】见解析.
【解析】(1)由题意,可得:, 解得:;
设购买A型设备台,则购买B型设备台,
由题意,可得:, 解得:.
∵取自然数, ∴为0,1,2.
∴该公式有三种购买方案:①购买10台B型设备;②购买1台A型设备,9台B型设
备;③购买2台A型设备,8台B型设备.
由题意,可得:,解得:, ∴的值为1或2.
当为1时,共需花费,
当为2时,共需花费,
∴最省钱的购买方案是购买1台A型设备,9台B型设备.
【总结】考察一次函数在实际问题中的应用,此题是有关最优方案的问题,解题时注意进行讨论.
已知在直角坐标平面内,直线AB经过原点O和点(1,-2),点P是直线AB 上一点,若过点P向y轴作垂直,垂足为M,且OPM的面积为9,求点P的坐标.
【难度】★★★
【答案】或.
【解析】∵直线AB经过原点O和点(1,-2),
∴直线AB为正比例函数,解析式为.
设
∵△OPM的面积为, ∴,解得:
∴或.
【总结】考察面积的处理方法,注意点坐标和线段长的转换中正负号或绝对值的添法.
如图,在梯形ΑBCD中,ΑB=CD=5,ΑD=7,BC=13,E为ΑD上一定点,ΑE=4, 动点P从D出发沿着DC向C点移动,设点P移动的距离为x,ΑPE的面积为y,
求y与x的函数解析式,并画出图象.
【难度】★★★
【答案】,图像略.
【解析】分别过点A、D作AM⊥BC,DN⊥BC,垂足分别为M、N.
可得:,.
∵,, ∴,即,
∴, ∵,即,∴, ∴.
【总结】考察面积中同底等高的处理方法.
在平面直角坐标系中,函数y=2x+12的图像分别交x轴、y轴于A、B两点.过 点A的直线交y轴正半轴于点M,且点M为线段OB的中点.
求直线AM的解析式;
试在直线AM上找一点P,使得,求出点P的坐标.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵函数y=2x+12的图像分别交x轴、y轴于A、B两点,
∴,.
∵点M为线段OB的中点,
∴.
∴利用待定系数法,可得直线AM的解析式为:;
∵, ∴,∴,
即O到直线AB的距离和P到直线AB的距离相等,
∴
∴直线OP的解析式为
∵点P在直线AM上,
∴令,解得:.
∴点P的坐标为.
【总结】考察一次函数解析式的求法和同底等高的两个三角形面积相等的运用.
如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的
坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;
(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;
(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时t的值?
【难度】★★★
【答案】见解析.
【解析】(1)由题意可知,点B坐标为,
∴,
由,得:,此时P在CB上;
∵, ∴,
∴;
经分析,可知点P只能在AB或OC上.
当点P在AB边上时,设点P的坐标为,
由,得:,解得:,此时,
当点P在OC上时,设点P的坐标为,
由得:,解得:,
此时.
∴在7秒或者秒时,线段PD将梯形COAB的面积分成1:3的两部分.
【总结】本题综合性较强,主要考察勾股定理和直角梯形的性质的综合运用,注意认真分析题意.
(1)若是关于x的一次函数,则m的值?
(2)可能是正比例函数吗?可能是反比例函数吗?如果是,求出m 的值.
【难度】★
【答案】见解析.
【解析】(1)由或,∴;
当函数为正比例函数时,且,所以不可能为正比例函数;
当函数为反比例函数时,且,所以不可能是反比例函数.
【总结】考察正比例函数、反比例函数的定义.
在下列函数解析式中,属于一次函数的是( )
(1) (2)
(3) (4)
A.(1) B.(1)(3) C.(1)(2)(3) D.全部都是
【难度】★
【答案】C
【解析】形如(,为常数).
【总结】考察一次函数的定义.
如果一次函数的图像经过一、二、四象限,那么的大致图像为( ).
【难度】★
【答案】B
【解析】∵一次函数的图像经过一、二、四象限,∴,
∴经过一、三、四象限.
【总结】考察一次函数的图像及性质.
已知函数y=,点P为图象上的任意一点,过P作PA⊥x轴A,PB⊥y轴于B,则APB的面积为_______________.
【难度】★
【答案】4
【解析】矩形OAPB的面积为8,△APB的面积矩形的一半.
【总结】考察反比例函数的面积问题的处理方法.
已知y1与成正比例,y2与3x成反比例,,当x=1时,y=4,当x=-1时,y=0,求y和x的函数关系式.
【难度】★
【答案】.
【解析】∵y1与成正比例,y2与3x成反比例,
∴设,, ∴
∵当x=1时,y=4;当x=-1时,y=0, ∴, 解得:,
∴y和x的函数关系式为:.
【总结】考察正比例和反比例的概念,并且考查了复合函数解析式的确定.
若A(a1,b1),B(a2,b2)是反比例函数图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
A.b1<b2 B.b1 =b2 C.b1>b2 D.大小不确定
【难度】★★
【答案】D
【解析】反比例函数在每个象限里面随着的增大而增大.因为A、B两点不确定
在哪个象限,所以不确定纵坐标的大小关系.
【总结】考察反比例函数的增减性,注意要分象限.
如图,已知点A是一次函数y=x的图象与反比例函数的图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么AOB的面积为( )
A.2 B. C. D.
【难度】★★
【答案】C
【解析】∵点A是一次函数y=x的图象与反比例函数的图象在
第一象限内的交点,∴,∴,∴,∴
∵,∴, ∴, 故选C.
【总结】考察函数交点的求法,从而求出三角形的面积.
为了鼓励小强勤做家务,培养他的劳动意识,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费为y元,则y(元)和x(小时)之间的函数图像如图所示.
(1)根据图像,请你写出小强每月的基本生活费为多少元;父母是如何奖励小强家务劳动的?
(2)写出当0≤x≤20时,相对应的y与x之间的函数关系式;
(3)若小强5月份希望有250元费用,则小强4月份需做家务多少时间?
【难度】★★
【答案】见解析.
【解析】(1)小强每月的基本生活费为150元;如果小强每月家务劳动时间不超过20小时,
每小时奖励2.5元;如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5
元奖励,超过部分按每小时4元奖励.
设直线方程为,
∵当时,图像经过
∴, 解得:,
∴y与x之间的函数关系式为:;
(3)当时,图像经过点,
∴, 解得:, ∴
则有题意可得:, 解得:
∴当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
【总结】考察一次函数在实际问题中的运用.
现有一个种植总面积为540m2的矩形塑料温棚,分垄间隔种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物不低于10垄,又不超过14垄(垄数为整数),它们的占地面积、产量、利润分别如下:
占地面积(m2/垄) 产量(千克/垄) 利润(元/千克)
西红柿 30 160 1.1
草莓 15 50 1.6
若草莓共种植了x垄,通过计算说明共有几种种植方案?分别是哪几种?
在几种种植方案中.哪种方案获利最大?最大的利润是多少?
【难度】★★★
【答案】见解析
【解析】(1)根据题意西红柿种了垄,则,解得:
∵,且是正整数,∴,
∴共有三种种植方案:①草莓种植12垄,西红柿种植12垄;②草莓种植13垄,西红
柿种植11垄;③草莓种植14垄,西红柿种植10垄;
设种植草莓和西红柿共可获得利润元,
则
∵随着的增大而减小,∴取最小值12时,有最大值为3072元.
即草莓种植12垄,西红柿种植12垄时,有最大利润为3072元.
【总结】考察一元一次不等式与一次函数的综合应用.
在反比例函数的图像上有不重合的两点A、B,且A点的纵坐标是2,B点的横坐标是2,BB'和AA'都垂直于x轴,B',A'为垂足.(1)求A点的横坐标;
(2)求的值;(3)求的值.
【难度】★★★
【答案】(1)4;(2)4;(3)6.
【解析】(1)∵A、B两点都在反比例函数的图像上,且A点的纵坐标是2,
∴A点的横坐标是4;
(2)由题意,可得:;
(3)
.
在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线平行.
(1)求:直线l的函数解析式及点B的坐标;
(2)如直线l上有一点M(a,-6),过点M作x轴的垂线,交直线于点N,在线段MN上求一点P,使PAB是直角三角形,请求出点P的坐标.
【难度】★★★
【答案】(1),;(2)或.
【解析】(1)∵直线l与直线平行,
∴设直线l的解析式为,
∵直线l经过点A(2,-3),
∴,
∴直线l的解析式为,
∴点B的坐标为;
∵直线l上有一点M(a,-6), ∴,
则可设,
∵, ∴的取值范围是.
当AB为斜边时,
∴,
解得:,
∴点P的坐标为;
当PB为斜边时,
∴,
解得:, ∴点P的坐标为;
当PA为斜边时,,
∴,解得:,舍去
综上所述,点P的坐标为或.
【总结】考察一次函数的解析式求法和直角三角形分类讨论,本题综合性较强,注意认真分析.
教师
日期
学生
课程编号
课型 新课
课题 函数的复习
教学目标
熟悉正反比例及一次函数的概念和性质 能利用函数的性质解决相应的问题即求角或者边之间的关系
能够运动数形结合的思想解决几何背景下的函数问题.
教学重点
熟练的运用函数的性质
运用一次函数模型解决实际问题.
运用一次函数的图像与性质求解初步几何问题.
教学安排
版块 时长
1 正反比例函数 20min
2 一次函数 30min
3 函数的综合 50min
4 作业 20min
正比例函数:y=kx(k≠0);图像是一条直线,与坐标轴仅有一个交点;k>0时,随着x
的逐渐增大,函数值y的值越来越大;k<0时,随着x的逐渐增大,函数值y的值越来
越小.
反比例函数:(k≠0),图像是双曲线,与坐标轴无交点;k>0时,在每一象限内,
随着x的逐渐增大,函数值y的值越来越小;k<0时,在每一象限内,随着x的逐渐增
大,函数值y的值越来越大.
(1)正方形的周长c与正方形的对角线长a_______正比例(填“成”或“不成”);
(2)已知正比例函数的自变量x减少2时,对应函数的值增加3,则这个函数的解析式为________________.
(1)如果y=kx+2k+x是正比例函数,求k的值;
(2)如果是反比例函数,求m的值.
(1)正比例函数经过第___________象限,y随x增大而_________;
(2)反比例函数经过第___________象限,在同一象限内,y随x增大而_________.
已知正比例函数y=k1x,函数值y随着x的增大而减小,反比例函数y=(k2<0),它们在同一直角坐标系中的图象大致是( ).
(1)已知,且与x成正比例,与x+3成正比例,当x=1时,y=-1,当x=3时,y=9,求x=5时,y的值;
(2)已知y与x成反比例关系,且x=2时,y=-3a;当x=a+1时,y=6.求y与x之间的函数解析式.
已知正比例函数的图像上一点P的横坐标是2,作PD⊥x轴(O是坐标原点,D是垂足),OPD的面积是6,求这个正比例函数的解析式.
已知如图,点A,B是反比例函数y=图像上的点,分别经过A,B两点向x轴、y轴做垂线段,若_________(指的是空白矩形的面积).
已知A(0,4)、B(6,4)、C(6,0)三点,经过原点的一条直线把矩形OABC的面积分成1:2两部分,求这条直线的函数解析式.
在平面直角坐标系中,O为坐标原点,点A的坐标为(1,0),在直线上取一点P,使得OAP是等腰三角形,求所有满足条件的点P的坐标.
已知如图,矩形OABC的顶点B(m,2)在正比例函数的图像上,点A在x轴上,点C在y轴上,反比例函数的图像过BC边上点M,与AB边交于点N,且BM=3CM,求此反比例函数的解析式及点N的坐标.
正比例函数的图像与反比例函数的图像相交于点、(如图),点在第一象限,且点的横坐标为,作轴,垂足为点,.
(1)求点的坐标;
(2)求这两个函数的解析式;
(3)如果是以为腰的等腰三角形,且点在轴上,求点的坐标.
如图所示,已知正方形ABCD的边长是3厘米,动点P从点B出发,沿BCDA方向运动至点A停止.点P的运动的路程为x厘米,ABP的面积为y平方厘米.
当点P在BC上运动时,求y关于x的解析式及定义域;
当点P在CD上运动时,求y关于x的解析式及其定义域;
当x取何值时,ABP的面积为1.5平方厘米?
1.函数的概念和图像及性质
(1)定义:解析式形如的函数叫做一次函数.
(2)一次函数的图象满足:
①形状是一条直线;②始终经过(0,b)和(,0)两点;
(3)定义:直线与y轴的交点坐标是,截距是b;
(4)一次函数,当时,函数值y随自变量x的值增大而增大;当 时,函数值y随自变量x的值增大而减小.
2.函数的应用
(1)实际问题;
(2)数形结合类.
(1)已知一次函数,当x=-3时,y=1;当x=2时,y=-6,求这个一次函数的解析式;
(2)已知一次函数y=f(x),且f(-1)=-3,f(1)=1,求函数f(x)的解析式.
(1)若一次函数y=k(1-x)+3的图像在y轴上的截距是-5,求这个函数解析式;
(2)若一次函数的图像经过原点,求k的值.
(1)若直线y=kx+b与直线y=-2x+4无交点,且直线y=kx+b与x轴的交点是
(3,0),求此函数解析式;
(2)已知一次函数的图像经过点(1,-2)、(-2,1).求这个一次函数的解析式.
(1)若把函数的图像向下平移4个单位,再向右平移2个单位,求平移
后的函数解析式;
(2)若一次函数的图像向下平移4个单位,再向右平移2个单位得到的函数解析式是,求平移前的函数解析式.
已知直线y=kx+4经过点P(1,m),且平行于直线y=-2x+1,它与x轴相交于点A,求OPA的面积.
已知一次函数的自变量的取值范围是,相应的函数值的范围是,求这个函数的解析式.
已知直线l过点(-2,4),且与两坐标轴围成一个等腰三角形,
(1)求这个一次函数的解析式;
(2)所得三角形的周长及面积.
某中学初二年级准备购买10只米奇品牌的笔袋,每只笔袋配x(x≥3)支水笔作为奖品.已知A、B两家超市都有这个牌子的笔袋和水笔出售,而且每只笔袋的标价都为20元,每只水笔的标价都为1元,现两家超市正在促销,A超市所有商品均打九折销售,而B超市买1只笔袋送3支水笔,若仅考虑购买笔袋和水笔的费用,请解答下列的问题:
如果只在某一家超市购买所需笔袋和水笔,那么去哪家超市购买更合算?
当x=12时,请设计最省钱的购买方案.
若直线过与的交点A,与y轴于B,交x轴于C,若,求直线y=的解析式.
已知反比例函数和一次函数,其中一次函数的图像经过点
(k,5).
试求反比例函数的解析式;
若点A在第一象限,且同时在上述两个函数的图像上,求点A的坐标.
【难度】★★
【答案】(1);(2).
【解析】(1)∵一次函数经过点(k,5),∴,∴点坐标为(3,5),
又因为这个点在反比例函数上,所以反比例函数的解析式为;
令,解得:,,代入可得:,,
∵点A在第一象限,∴.
【总结】考察反比例解析式的求法和交点坐标的求法.
如图,一次函数的图像与x轴、y轴分别交于点A、B两点,且与反比例函数的图像在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
求点A、B、D的坐标;
求一次函数和反比例函数的解析式.
【难度】★★
【答案】(1);
(2),.
【解析】(1)∵OA=OB=OD=1,∴;
(2)∵一次函数的图像与x轴、y轴分别交于点A、B两点,
∴;
∵C在上,∴.
∵在上, ∴.
【总结】考察反比例函数和一次函数的解析式求法.
如图,一次函数的图像与与反比例函数的图像交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,
求:(1)一次函数的解析式;(2)AOB的面积.
【难度】★★
【答案】(1);(2)6.
【解析】(1)∵点A的横坐标和点B的纵坐标都是-2,
且两点都在反比例函数的图像上,
∴,
∵两点都在一次函数上,
∴, ∴,
∴一次函数解析式为:;
∵一次函数与轴的交点为,
∴.
【总结】考察反比例函数和一次函数解析式的求法及三角形面积的求法.
已知点A(m,2m)(其中m>0)在双曲线上,直线y=kx+b过点A,并且与坐标轴正方向所围成的三角形的面积是18,求直线的解析式.
【难度】★★
【答案】或.
【解析】∵点A(m,2m)(其中m>0)在双曲线上,
∴,∴或,∵,∴,∴
∵直线y=kx+b过点A,∴
∵直线y=kx+b与坐标轴正方向所围成的三角形的面积是18,
∴,解得:或
当时,,直线的解析式为;
当时,,直线的解析式为.
【总结】考察反比例函数、一次函数解析式的求法和面积问题的处理方法.
已知一次函数与反比例函数的图像交于点P(-3,2)、Q(2,-3).
求这两个函数的函数解析式;
在给定的直角坐标系中,画出这两个函数的大致图像;
当x为何值时,一次函数的值大于反比例函数的值?当x为何值时,一次函数的值小于反比例函数的值?
【难度】★★
【答案】见解析.
【解析】(1)反比例的函数解析式为
设一次函数的解析式为,
则可得:,
解得:,
所以一次函数解析式为;
(2)如右图;
当或时,一次函数的值大于反比例函数的值;
当或时,一次函数的值小于反比例函数的值.
【总结】考察反比例函数、一次函数的解析式的求法和函数性质的分析.
已知一次函数;
(1)求证:无论取何实数,函数的图像恒过一定点;
(2)当在内变化时,在内变化,求的值.
【难度】★★★
【答案】(1)见解析;(2).
【解析】(1),当,即时,,
∴无论取何实数,函数的图像恒过一定点;
当时,, 解得:;
当时,, ∴解不等式后不存在这样的m值,
所以.
【总结】考察解析式图像恒过一定点的条件和一次函数的增减性的运用.
如图所示,双曲线在第一象限的一支上有一点C(1,5),过点C的直线与x轴交于点A(a,0)、与y轴交于点B.
求点A的横坐标a与k之间的函数关系式;
当该直线与双曲线在第一象限的另一交点D的横坐标是9时,求△COD的面积.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵点C(1,5),A(a,0)在上,
∴,,
∴,
∵D的横坐标是9,且双曲线,
∴.
分别过点C作CE⊥轴,过点D作DF⊥轴,
则
.
【总结】考察反比例函数与一次函数解析式的求法,图中由于△OCE和△OFD的面积相等,则△OCD的面积与梯形CEFD的面积相等.
(1)y与x成正比例,且x=4时,y=-4,那么y与x之间的函数关系式为__________;
(2)y+1与z成正比例,比例系数为2,z与x-1成正比例,当x=-1时,y=7,那么y 与x的函数关系式为____________
【难度】★
【答案】(1);(2).
【解析】(1)由题意可知,函数关系式为:;
∵y+1与z成正比例,比例系数为2,
∴;
∵z与x-1成正比例,∴设,
∴,
∵当x=-1时,y=7,∴,
∴.
【总结】考察正比例的定义.
已知y是x的函数,y与x-1成正比例,如果这个函数的图象经过点(α,α)(α≠0),
则它的图象大致是( )
【难度】★
【答案】B
【解析】∵y与x-1成正比例,∴,则此函数为一次函数,且不经过原点,
则选B.
【总结】考察正比例的定义和函数图像的画法.
已知y-3与x成正比例,且x=2时,y=7.
写出y与x的函数关系式;
计算x=4时y的值;
计算y=4时x的值.
【难度】★
【答案】(1);(2)11;(3).
【解析】(1)设, ∵x=2时,y=7,∴, ∴;
当时,;
当时,.
【总结】考察正比例的定义,及根据其中一个变量的值求另一个变量的值.
已知一次函数的图像交轴于A(,0),交正比例函数的图像于点B,且点B 在第三象限,它的横坐标为,的面积为6,求正比例函数和一次函数的解析 式.
【难度】★★
【答案】正比例函数:;一次函数:.
【解析】∵的面积为6,
∴, ∴
∵点B在第三象限,它的横坐标为,
∴
则正比例函数的解析式为.
设一次函数的解析式为
则,∴,
∴一次函数的解析式为
【总结】考察一次函数的解析式的求法和面积的处理方法.
已知函数y=的图象和两条直线y=x、y=2x在第一象限内分别交于P1和P2两点, 过点P1分别作x轴、y轴的垂线P1Q1、P1R1,垂足分别为Q1、R1;过点P2分别作x轴、 y轴的垂线P2Q2、P2R2,垂足分别为Q2、R2,求矩形OQ1P1R1和OQ2P2R2的周长并比 较它们的大小.
【难度】★★
【答案】,
,
.
【解析】∵是函数和在第一象限的交点,
∴,∴,∴
∵是函数和在第一象限的交点
∴,∴,∴
∴,
∵,∴.
【总结】考察函数交点的求法及几何图形的周长及大小比较.
如图,正方形的面积为9,点O为坐标原点,点B在函数 的图象上,点P(m,n)是函数的图象上任意一点,边点P分别作 x轴、y轴的垂线.垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面 积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(1)B点的坐标是___________;=__________;
(2)时,P的坐标是___________;
(3)求出S关于m的函数关系式.
【难度】★★
【答案】(1),;(2)或;
(3)或.
【解析】(1)由正方形的面积为9,得,
∴反比例函数的解析式为:;
当点P在点B右侧时,
∵, ∴, ∴的纵坐标为.
∵点在函数的图像上,∴;
当点P在点B左侧时,同理可得P点的坐标为,
综上,点P的坐标为或;
∵P(m,n)是函数上, ∴设.
当点在点的右侧时,, ∴;
当点在点的左侧时,,∴.
【总结】考察反比例函数的解析式的求法和面积的处理方法,注意分类讨论.
为了更好的治理某个湖水水质,保护环境,治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:
A型 B型
价格(万元/台) a b
处理污水量(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买 3台B型设备少6万元.
求a、b的值;
经预算:治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
在(2)问的条件下,若每月要求处理该湖泊的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
【难度】★★
【答案】见解析.
【解析】(1)由题意,可得:, 解得:;
设购买A型设备台,则购买B型设备台,
由题意,可得:, 解得:.
∵取自然数, ∴为0,1,2.
∴该公式有三种购买方案:①购买10台B型设备;②购买1台A型设备,9台B型设
备;③购买2台A型设备,8台B型设备.
由题意,可得:,解得:, ∴的值为1或2.
当为1时,共需花费,
当为2时,共需花费,
∴最省钱的购买方案是购买1台A型设备,9台B型设备.
【总结】考察一次函数在实际问题中的应用,此题是有关最优方案的问题,解题时注意进行讨论.
已知在直角坐标平面内,直线AB经过原点O和点(1,-2),点P是直线AB 上一点,若过点P向y轴作垂直,垂足为M,且OPM的面积为9,求点P的坐标.
【难度】★★★
【答案】或.
【解析】∵直线AB经过原点O和点(1,-2),
∴直线AB为正比例函数,解析式为.
设
∵△OPM的面积为, ∴,解得:
∴或.
【总结】考察面积的处理方法,注意点坐标和线段长的转换中正负号或绝对值的添法.
如图,在梯形ΑBCD中,ΑB=CD=5,ΑD=7,BC=13,E为ΑD上一定点,ΑE=4, 动点P从D出发沿着DC向C点移动,设点P移动的距离为x,ΑPE的面积为y,
求y与x的函数解析式,并画出图象.
【难度】★★★
【答案】,图像略.
【解析】分别过点A、D作AM⊥BC,DN⊥BC,垂足分别为M、N.
可得:,.
∵,, ∴,即,
∴, ∵,即,∴, ∴.
【总结】考察面积中同底等高的处理方法.
在平面直角坐标系中,函数y=2x+12的图像分别交x轴、y轴于A、B两点.过 点A的直线交y轴正半轴于点M,且点M为线段OB的中点.
求直线AM的解析式;
试在直线AM上找一点P,使得,求出点P的坐标.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵函数y=2x+12的图像分别交x轴、y轴于A、B两点,
∴,.
∵点M为线段OB的中点,
∴.
∴利用待定系数法,可得直线AM的解析式为:;
∵, ∴,∴,
即O到直线AB的距离和P到直线AB的距离相等,
∴
∴直线OP的解析式为
∵点P在直线AM上,
∴令,解得:.
∴点P的坐标为.
【总结】考察一次函数解析式的求法和同底等高的两个三角形面积相等的运用.
如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的
坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;
(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;
(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时t的值?
【难度】★★★
【答案】见解析.
【解析】(1)由题意可知,点B坐标为,
∴,
由,得:,此时P在CB上;
∵, ∴,
∴;
经分析,可知点P只能在AB或OC上.
当点P在AB边上时,设点P的坐标为,
由,得:,解得:,此时,
当点P在OC上时,设点P的坐标为,
由得:,解得:,
此时.
∴在7秒或者秒时,线段PD将梯形COAB的面积分成1:3的两部分.
【总结】本题综合性较强,主要考察勾股定理和直角梯形的性质的综合运用,注意认真分析题意.
(1)若是关于x的一次函数,则m的值?
(2)可能是正比例函数吗?可能是反比例函数吗?如果是,求出m 的值.
【难度】★
【答案】见解析.
【解析】(1)由或,∴;
当函数为正比例函数时,且,所以不可能为正比例函数;
当函数为反比例函数时,且,所以不可能是反比例函数.
【总结】考察正比例函数、反比例函数的定义.
在下列函数解析式中,属于一次函数的是( )
(1) (2)
(3) (4)
A.(1) B.(1)(3) C.(1)(2)(3) D.全部都是
【难度】★
【答案】C
【解析】形如(,为常数).
【总结】考察一次函数的定义.
如果一次函数的图像经过一、二、四象限,那么的大致图像为( ).
【难度】★
【答案】B
【解析】∵一次函数的图像经过一、二、四象限,∴,
∴经过一、三、四象限.
【总结】考察一次函数的图像及性质.
已知函数y=,点P为图象上的任意一点,过P作PA⊥x轴A,PB⊥y轴于B,则APB的面积为_______________.
【难度】★
【答案】4
【解析】矩形OAPB的面积为8,△APB的面积矩形的一半.
【总结】考察反比例函数的面积问题的处理方法.
已知y1与成正比例,y2与3x成反比例,,当x=1时,y=4,当x=-1时,y=0,求y和x的函数关系式.
【难度】★
【答案】.
【解析】∵y1与成正比例,y2与3x成反比例,
∴设,, ∴
∵当x=1时,y=4;当x=-1时,y=0, ∴, 解得:,
∴y和x的函数关系式为:.
【总结】考察正比例和反比例的概念,并且考查了复合函数解析式的确定.
若A(a1,b1),B(a2,b2)是反比例函数图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
A.b1<b2 B.b1 =b2 C.b1>b2 D.大小不确定
【难度】★★
【答案】D
【解析】反比例函数在每个象限里面随着的增大而增大.因为A、B两点不确定
在哪个象限,所以不确定纵坐标的大小关系.
【总结】考察反比例函数的增减性,注意要分象限.
如图,已知点A是一次函数y=x的图象与反比例函数的图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么AOB的面积为( )
A.2 B. C. D.
【难度】★★
【答案】C
【解析】∵点A是一次函数y=x的图象与反比例函数的图象在
第一象限内的交点,∴,∴,∴,∴
∵,∴, ∴, 故选C.
【总结】考察函数交点的求法,从而求出三角形的面积.
为了鼓励小强勤做家务,培养他的劳动意识,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费为y元,则y(元)和x(小时)之间的函数图像如图所示.
(1)根据图像,请你写出小强每月的基本生活费为多少元;父母是如何奖励小强家务劳动的?
(2)写出当0≤x≤20时,相对应的y与x之间的函数关系式;
(3)若小强5月份希望有250元费用,则小强4月份需做家务多少时间?
【难度】★★
【答案】见解析.
【解析】(1)小强每月的基本生活费为150元;如果小强每月家务劳动时间不超过20小时,
每小时奖励2.5元;如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5
元奖励,超过部分按每小时4元奖励.
设直线方程为,
∵当时,图像经过
∴, 解得:,
∴y与x之间的函数关系式为:;
(3)当时,图像经过点,
∴, 解得:, ∴
则有题意可得:, 解得:
∴当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
【总结】考察一次函数在实际问题中的运用.
现有一个种植总面积为540m2的矩形塑料温棚,分垄间隔种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物不低于10垄,又不超过14垄(垄数为整数),它们的占地面积、产量、利润分别如下:
占地面积(m2/垄) 产量(千克/垄) 利润(元/千克)
西红柿 30 160 1.1
草莓 15 50 1.6
若草莓共种植了x垄,通过计算说明共有几种种植方案?分别是哪几种?
在几种种植方案中.哪种方案获利最大?最大的利润是多少?
【难度】★★★
【答案】见解析
【解析】(1)根据题意西红柿种了垄,则,解得:
∵,且是正整数,∴,
∴共有三种种植方案:①草莓种植12垄,西红柿种植12垄;②草莓种植13垄,西红
柿种植11垄;③草莓种植14垄,西红柿种植10垄;
设种植草莓和西红柿共可获得利润元,
则
∵随着的增大而减小,∴取最小值12时,有最大值为3072元.
即草莓种植12垄,西红柿种植12垄时,有最大利润为3072元.
【总结】考察一元一次不等式与一次函数的综合应用.
在反比例函数的图像上有不重合的两点A、B,且A点的纵坐标是2,B点的横坐标是2,BB'和AA'都垂直于x轴,B',A'为垂足.(1)求A点的横坐标;
(2)求的值;(3)求的值.
【难度】★★★
【答案】(1)4;(2)4;(3)6.
【解析】(1)∵A、B两点都在反比例函数的图像上,且A点的纵坐标是2,
∴A点的横坐标是4;
(2)由题意,可得:;
(3)
.
在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线平行.
(1)求:直线l的函数解析式及点B的坐标;
(2)如直线l上有一点M(a,-6),过点M作x轴的垂线,交直线于点N,在线段MN上求一点P,使PAB是直角三角形,请求出点P的坐标.
【难度】★★★
【答案】(1),;(2)或.
【解析】(1)∵直线l与直线平行,
∴设直线l的解析式为,
∵直线l经过点A(2,-3),
∴,
∴直线l的解析式为,
∴点B的坐标为;
∵直线l上有一点M(a,-6), ∴,
则可设,
∵, ∴的取值范围是.
当AB为斜边时,
∴,
解得:,
∴点P的坐标为;
当PB为斜边时,
∴,
解得:, ∴点P的坐标为;
当PA为斜边时,,
∴,解得:,舍去
综上所述,点P的坐标为或.
【总结】考察一次函数的解析式求法和直角三角形分类讨论,本题综合性较强,注意认真分析.
初二数学寒假班(学生版)
教师
日期
学生
课程编号
课型 新课
课题 函数的复习
教学目标
熟悉正反比例及一次函数的概念和性质 能利用函数的性质解决相应的问题即求角或者边之间的关系
能够运动数形结合的思想解决几何背景下的函数问题.
教学重点
熟练的运用函数的性质
运用一次函数模型解决实际问题.
运用一次函数的图像与性质求解初步几何问题.
教学安排
版块 时长
1 正反比例函数 20min
2 一次函数 30min
3 函数的综合 50min
4 作业 20min
正比例函数:y=kx(k≠0);图像是一条直线,与坐标轴仅有一个交点;k>0时,随着x
的逐渐增大,函数值y的值越来越大;k<0时,随着x的逐渐增大,函数值y的值越来
越小.
反比例函数:(k≠0),图像是双曲线,与坐标轴无交点;k>0时,在每一象限内,
随着x的逐渐增大,函数值y的值越来越小;k<0时,在每一象限内,随着x的逐渐增
大,函数值y的值越来越大.
(1)正方形的周长c与正方形的对角线长a_______正比例(填“成”或“不成”);
(2)已知正比例函数的自变量x减少2时,对应函数的值增加3,则这个函数的解析式为________________.
【难度】★
【答案】(1)成;(2).
【解析】(1)正方形的对角线长为,则正方形的边长为,则,
为一定值,所以成正比例.
设,则由题意,可得:,解得:,
从而可得这个函数的解析式为.
【总结】考察正比例的定义和正比例函数解析式的求法.
(1)如果y=kx+2k+x是正比例函数,求k的值;
(2)如果是反比例函数,求m的值.
【难度】★
【答案】(1)0;(2)4.
【解析】(1)因为是正比例函数,所以,解得:;
(2)因为函数是反比例函数,
所以可得, ,∴.
【总结】考察正比例函数和反比例函数的定义,注意比例系数要不为零.
(1)正比例函数经过第___________象限,y随x增大而_________;
(2)反比例函数经过第___________象限,在同一象限内,y随x增大而_________.
【难度】★
【答案】(1)一、三,增大;(2)一、三,减小.
【解析】(1)因为是正比例函数,所以可得,解得:,
∴函数解析式为,图像过一、三象限,y随x的增大而增大;
因为是反比例函数,所以可得,解得:,
∴函数解析式为,图像过一、三象限,y随x的增大而减小.
【总结】考察正、反比例函数的概念和性质,注意比例系数不为零.
已知正比例函数y=k1x,函数值y随着x的增大而减小,反比例函数y=(k2<0),它们在同一直角坐标系中的图象大致是( ).
【难度】★
【答案】A
【解析】由题意可知:正比例函数在二、四象限;反比例函数在二、四象限,故选A.
【总结】考察正、反比例函数的图像及性质.
(1)已知,且与x成正比例,与x+3成正比例,当x=1时,y=-1,当x=3时,y=9,求x=5时,y的值;
(2)已知y与x成反比例关系,且x=2时,y=-3a;当x=a+1时,y=6.求y与x之间的函数解析式.
【难度】★★
【答案】(1)19;(2).
【解析】(1)设,,则,
由题意可得:,解得:,∴
∴当时,;
设,则可得:,∴, ∴.
【总结】本题一反面考察了复合函数解析式的确定,另一方面考查了反比例函数的概念.
已知正比例函数的图像上一点P的横坐标是2,作PD⊥x轴(O是坐标原点,D是垂足),OPD的面积是6,求这个正比例函数的解析式.
【难度】★★
【答案】或.
【解析】由题意可得:,,则,∴或
则正比例函数的解析式为或
【总结】考察正比例函数解析式的求法,注意长度转成点坐标需要注意正负.
已知如图,点A,B是反比例函数y=图像上的点,分别经过A,B两点向x轴、y轴做垂线段,若_________(指的是空白矩形的面积).
【难度】★★
【答案】4
【解析】∵,,,
∴,,∴.
【总结】考察反比例函数的面积问题.过反比例函数
上任意一点作x轴、y轴的垂线,构成的矩形的面积为.
已知A(0,4)、B(6,4)、C(6,0)三点,经过原点的一条直线把矩形OABC的面积分成1:2两部分,求这条直线的函数解析式.
【难度】★★
【答案】或.
【解析】矩形OABC的面积为24,因为直线将矩形分成1:2两部分,则其中较小部分的面
积为8.当经过原点的一条直线与AB相交时,其交点为D,则,则,
∴,此时正比例函数解析式为;
当经过原点的一条直线与CB相交时,其交点为E,则,则,
∴,此时正比例函数解析式为.
【总结】考察面积的处理方法和正比例函数解析式的求法,注意分类讨论.
在平面直角坐标系中,O为坐标原点,点A的坐标为(1,0),在直线上取一点P,使得OAP是等腰三角形,求所有满足条件的点P的坐标.
【难度】★★★
【答案】或或或 .
【解析】当时,P点在OA的线段垂直平分线上,则P点的横坐标为,
代入函数解析式可得纵坐标为,∴;当时,设,
则,∴,∴或;
当时,设, 则,∴,
∴或,其中与原点重合舍去.
综上所述,满足题意的点坐标为或或或.
已知如图,矩形OABC的顶点B(m,2)在正比例函数的图像上,点A在x轴上,点C在y轴上,反比例函数的图像过BC边上点M,与AB边交于点N,且BM=3CM,求此反比例函数的解析式及点N的坐标.
【难度】★★★
【答案】,.
【解析】∵B(m,2)在正比例函数的图像上,∴.
∵BM=3CM,∴,∴,
∴反比例函数的解析式为,∴.
【总结】考察反比例函数的解析式的求法和点坐标的求法.
正比例函数的图像与反比例函数的图像相交于点、(如图),点在第一象限,且点的横坐标为,作轴,垂足为点,.
(1)求点的坐标;
(2)求这两个函数的解析式;
(3)如果是以为腰的等腰三角形,且点在轴上,求点的坐标.
【难度】★★★
【答案】见解析.
【解析】(1)由题可知,点A坐标为:;
(2)反比例函数解析式为;正比例函数解析式为;
(3)当时,,则或,
当时,由等腰三角形三线合一性质可得:,∴
综上所述:或或.
【总结】考察正反比例函数解析式的求法和等腰三角形的分类讨论.
如图所示,已知正方形ABCD的边长是3厘米,动点P从点B出发,沿BCDA方向运动至点A停止.点P的运动的路程为x厘米,ABP的面积为y平方厘米.
当点P在BC上运动时,求y关于x的解析式及定义域;
当点P在CD上运动时,求y关于x的解析式及其定义域;
当x取何值时,ABP的面积为1.5平方厘米?
【难度】★★★ 【答案】见解析.
【解析】(1)当点P在BC上运动时,
∴;
当点P在CD上运动时,,
∴;
,∴
当P在BC边上时,;当P在DA边上时,.
1.函数的概念和图像及性质
(1)定义:解析式形如的函数叫做一次函数.
(2)一次函数的图象满足:
①形状是一条直线;②始终经过(0,b)和(,0)两点;
(3)定义:直线与y轴的交点坐标是,截距是b;
(4)一次函数,当时,函数值y随自变量x的值增大而增大;当 时,函数值y随自变量x的值增大而减小.
2.函数的应用
(1)实际问题;
(2)数形结合类.
(1)已知一次函数,当x=-3时,y=1;当x=2时,y=-6,求这个一次函数的解析式;
(2)已知一次函数y=f(x),且f(-1)=-3,f(1)=1,求函数f(x)的解析式.
【难度】★
【答案】(1);(2).
【解析】(1)由题意可得:,解得:,
则一次函数解析式为;
设,
由题意可得:, 解得:,
则一次函数解析式为.
【总结】考察利用待定系数法求一次函数解析式的求解析式.
(1)若一次函数y=k(1-x)+3的图像在y轴上的截距是-5,求这个函数解析式;
(2)若一次函数的图像经过原点,求k的值.
【难度】★
【答案】(1);(2).
【解析】(1)若一次函数y=k(1-x)+3的截距为,则,
所以这个函数的解析式为
∵图像过原点,
∴且, ∴
【总结】考察一次函数的截距等概念.
(1)若直线y=kx+b与直线y=-2x+4无交点,且直线y=kx+b与x轴的交点是
(3,0),求此函数解析式;
(2)已知一次函数的图像经过点(1,-2)、(-2,1).求这个一次函数的解析式.
【难度】★
【答案】(1);(2).
【解析】(1)∵直线y=kx+b与直线y=-2x+4无交点,
∴直线y=kx+b与直线y=-2x+4平行,∴,故解析式为,
∵直线y=kx+b与x轴的交点是(3,0),∴,
∴函数解析式为;
(2)设,
由题意可得:,解得:,则一次函数解析式为.
【总结】考察一次函数解析式的求法,注意两直线的位置关系与k和b的关系.
(1)若把函数的图像向下平移4个单位,再向右平移2个单位,求平移
后的函数解析式;
(2)若一次函数的图像向下平移4个单位,再向右平移2个单位得到的函数解析式是,求平移前的函数解析式.
【难度】★★
【答案】(1);(2).
【解析】(1)利用平移规则,可知平移后的函数解析式为:;
利用平移规则,可知平移后的函数解析式为:.
已知直线y=kx+4经过点P(1,m),且平行于直线y=-2x+1,它与x轴相交于点A,求OPA的面积.
【难度】★★
【答案】2.
【解析】∵直线y=kx+4平行于直线y=-2x+1, ∴, 则,
则它与x轴相交于点.
∵直线经过点P(1,m),∴, ∴.
∴△POA的面积为:.
【总结】考察一次函数的图像性质及与三角形面积的结合.
已知一次函数的自变量的取值范围是,相应的函数值的范围是,求这个函数的解析式.
【难度】★★
【答案】或.
【解析】当时,则有, 解得:,
这个函数解析式为;
当时,则有,解得:,
这个函数解析式为.
【总结】考察一次函数的性质,注意此类题要有两种情况的分类讨论.
已知直线l过点(-2,4),且与两坐标轴围成一个等腰三角形,
(1)求这个一次函数的解析式;
(2)所得三角形的周长及面积.
【难度】★★
【答案】见解析.
【解析】设一次函数的解析式为,
∵函数图像与两坐标轴围成一个等腰三角形, ∴,则
当时,一次函数为,直线l过点(-2,4),∴,∴
与坐标轴的交点为,,此时周长为,面积为18;
当时,一次函数为,直线l过点(-2,4),∴,∴,
与坐标轴的交点为,,此时周长为,面积为2.
【总结】考察一次函数的性质,注意线段长与点坐标之间的转换.
某中学初二年级准备购买10只米奇品牌的笔袋,每只笔袋配x(x≥3)支水笔作为奖品.已知A、B两家超市都有这个牌子的笔袋和水笔出售,而且每只笔袋的标价都为20元,每只水笔的标价都为1元,现两家超市正在促销,A超市所有商品均打九折销售,而B超市买1只笔袋送3支水笔,若仅考虑购买笔袋和水笔的费用,请解答下列的问题:
如果只在某一家超市购买所需笔袋和水笔,那么去哪家超市购买更合算?
当x=12时,请设计最省钱的购买方案.
【难度】★★★
【答案】见解析.
【解析】(1)A家超市共付(x≥3);
B家超市共付(x≥3);
当时,则; 当时,则;
当时,则;
所以每只笔袋配10只笔时,A、B两家超市都一样;
每只笔袋配超过10只笔时,选A家超市更合算;
每只笔袋配超过10只但是不少于3只笔时,选B家超市更合算;
(2)当x=12时,即要10支笔袋,配120支笔.
设总费用为b,在A超市买a只笔袋,在B超市买(10-a)只,送了3(10-a)支笔,
则
故当时,总费用最少,为281元,
因此在B超市买10只笔袋,在A超市买90支水笔是最省钱的购买方案.
【总结】考察一次函数的应用.
若直线过与的交点A,与y轴于B,交x轴于C,若,求直线y=的解析式.
【难度】★★★
【答案】.
【解析】∵与的交点A为,与y轴交于点B,
交x轴于点C
又∵直线过A为, ∴,
∴过A作AE⊥x轴,垂足为E,
当时,
,
解得:(舍去)
当时,设直线AE与BC相交于F
∴
∵, ∴,
∴直线解析式为.
【总结】考察面积问题的处理方法,注意分类讨论.
已知反比例函数和一次函数,其中一次函数的图像经过点
(k,5).
试求反比例函数的解析式;
若点A在第一象限,且同时在上述两个函数的图像上,求点A的坐标.
【难度】★★
【答案】(1);(2).
【解析】(1)∵一次函数经过点(k,5),∴,∴点坐标为(3,5),
又因为这个点在反比例函数上,所以反比例函数的解析式为;
令,解得:,,代入可得:,,
∵点A在第一象限,∴.
【总结】考察反比例解析式的求法和交点坐标的求法.
如图,一次函数的图像与x轴、y轴分别交于点A、B两点,且与反比例函数的图像在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
求点A、B、D的坐标;
求一次函数和反比例函数的解析式.
【难度】★★
【答案】(1);
(2),.
【解析】(1)∵OA=OB=OD=1,∴;
(2)∵一次函数的图像与x轴、y轴分别交于点A、B两点,
∴;
∵C在上,∴.
∵在上, ∴.
【总结】考察反比例函数和一次函数的解析式求法.
如图,一次函数的图像与与反比例函数的图像交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,
求:(1)一次函数的解析式;(2)AOB的面积.
【难度】★★
【答案】(1);(2)6.
【解析】(1)∵点A的横坐标和点B的纵坐标都是-2,
且两点都在反比例函数的图像上,
∴,
∵两点都在一次函数上,
∴, ∴,
∴一次函数解析式为:;
∵一次函数与轴的交点为,
∴.
【总结】考察反比例函数和一次函数解析式的求法及三角形面积的求法.
已知点A(m,2m)(其中m>0)在双曲线上,直线y=kx+b过点A,并且与坐标轴正方向所围成的三角形的面积是18,求直线的解析式.
【难度】★★
【答案】或.
【解析】∵点A(m,2m)(其中m>0)在双曲线上,
∴,∴或,∵,∴,∴
∵直线y=kx+b过点A,∴
∵直线y=kx+b与坐标轴正方向所围成的三角形的面积是18,
∴,解得:或
当时,,直线的解析式为;
当时,,直线的解析式为.
【总结】考察反比例函数、一次函数解析式的求法和面积问题的处理方法.
已知一次函数与反比例函数的图像交于点P(-3,2)、Q(2,-3).
求这两个函数的函数解析式;
在给定的直角坐标系中,画出这两个函数的大致图像;
当x为何值时,一次函数的值大于反比例函数的值?当x为何值时,一次函数的值小于反比例函数的值?
【难度】★★
【答案】见解析.
【解析】(1)反比例的函数解析式为
设一次函数的解析式为,
则可得:,
解得:,
所以一次函数解析式为;
(2)如右图;
当或时,一次函数的值大于反比例函数的值;
当或时,一次函数的值小于反比例函数的值.
【总结】考察反比例函数、一次函数的解析式的求法和函数性质的分析.
已知一次函数;
(1)求证:无论取何实数,函数的图像恒过一定点;
(2)当在内变化时,在内变化,求的值.
【难度】★★★
【答案】(1)见解析;(2).
【解析】(1),当,即时,,
∴无论取何实数,函数的图像恒过一定点;
当时,, 解得:;
当时,, ∴解不等式后不存在这样的m值,
所以.
【总结】考察解析式图像恒过一定点的条件和一次函数的增减性的运用.
如图所示,双曲线在第一象限的一支上有一点C(1,5),过点C的直线与x轴交于点A(a,0)、与y轴交于点B.
求点A的横坐标a与k之间的函数关系式;
当该直线与双曲线在第一象限的另一交点D的横坐标是9时,求△COD的面积.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵点C(1,5),A(a,0)在上,
∴,,
∴,
∵D的横坐标是9,且双曲线,
∴.
分别过点C作CE⊥轴,过点D作DF⊥轴,
则
.
【总结】考察反比例函数与一次函数解析式的求法,图中由于△OCE和△OFD的面积相等,则△OCD的面积与梯形CEFD的面积相等.
(1)y与x成正比例,且x=4时,y=-4,那么y与x之间的函数关系式为__________;
(2)y+1与z成正比例,比例系数为2,z与x-1成正比例,当x=-1时,y=7,那么y 与x的函数关系式为____________
【难度】★
【答案】(1);(2).
【解析】(1)由题意可知,函数关系式为:;
∵y+1与z成正比例,比例系数为2,
∴;
∵z与x-1成正比例,∴设,
∴,
∵当x=-1时,y=7,∴,
∴.
【总结】考察正比例的定义.
已知y是x的函数,y与x-1成正比例,如果这个函数的图象经过点(α,α)(α≠0),
则它的图象大致是( )
【难度】★
【答案】B
【解析】∵y与x-1成正比例,∴,则此函数为一次函数,且不经过原点,
则选B.
【总结】考察正比例的定义和函数图像的画法.
已知y-3与x成正比例,且x=2时,y=7.
写出y与x的函数关系式;
计算x=4时y的值;
计算y=4时x的值.
【难度】★
【答案】(1);(2)11;(3).
【解析】(1)设, ∵x=2时,y=7,∴, ∴;
当时,;
当时,.
【总结】考察正比例的定义,及根据其中一个变量的值求另一个变量的值.
已知一次函数的图像交轴于A(,0),交正比例函数的图像于点B,且点B 在第三象限,它的横坐标为,的面积为6,求正比例函数和一次函数的解析 式.
【难度】★★
【答案】正比例函数:;一次函数:.
【解析】∵的面积为6,
∴, ∴
∵点B在第三象限,它的横坐标为,
∴
则正比例函数的解析式为.
设一次函数的解析式为
则,∴,
∴一次函数的解析式为
【总结】考察一次函数的解析式的求法和面积的处理方法.
已知函数y=的图象和两条直线y=x、y=2x在第一象限内分别交于P1和P2两点, 过点P1分别作x轴、y轴的垂线P1Q1、P1R1,垂足分别为Q1、R1;过点P2分别作x轴、 y轴的垂线P2Q2、P2R2,垂足分别为Q2、R2,求矩形OQ1P1R1和OQ2P2R2的周长并比 较它们的大小.
【难度】★★
【答案】,
,
.
【解析】∵是函数和在第一象限的交点,
∴,∴,∴
∵是函数和在第一象限的交点
∴,∴,∴
∴,
∵,∴.
【总结】考察函数交点的求法及几何图形的周长及大小比较.
如图,正方形的面积为9,点O为坐标原点,点B在函数 的图象上,点P(m,n)是函数的图象上任意一点,边点P分别作 x轴、y轴的垂线.垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面 积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(1)B点的坐标是___________;=__________;
(2)时,P的坐标是___________;
(3)求出S关于m的函数关系式.
【难度】★★
【答案】(1),;(2)或;
(3)或.
【解析】(1)由正方形的面积为9,得,
∴反比例函数的解析式为:;
当点P在点B右侧时,
∵, ∴, ∴的纵坐标为.
∵点在函数的图像上,∴;
当点P在点B左侧时,同理可得P点的坐标为,
综上,点P的坐标为或;
∵P(m,n)是函数上, ∴设.
当点在点的右侧时,, ∴;
当点在点的左侧时,,∴.
【总结】考察反比例函数的解析式的求法和面积的处理方法,注意分类讨论.
为了更好的治理某个湖水水质,保护环境,治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:
A型 B型
价格(万元/台) a b
处理污水量(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买 3台B型设备少6万元.
求a、b的值;
经预算:治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案?
在(2)问的条件下,若每月要求处理该湖泊的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
【难度】★★
【答案】见解析.
【解析】(1)由题意,可得:, 解得:;
设购买A型设备台,则购买B型设备台,
由题意,可得:, 解得:.
∵取自然数, ∴为0,1,2.
∴该公式有三种购买方案:①购买10台B型设备;②购买1台A型设备,9台B型设
备;③购买2台A型设备,8台B型设备.
由题意,可得:,解得:, ∴的值为1或2.
当为1时,共需花费,
当为2时,共需花费,
∴最省钱的购买方案是购买1台A型设备,9台B型设备.
【总结】考察一次函数在实际问题中的应用,此题是有关最优方案的问题,解题时注意进行讨论.
已知在直角坐标平面内,直线AB经过原点O和点(1,-2),点P是直线AB 上一点,若过点P向y轴作垂直,垂足为M,且OPM的面积为9,求点P的坐标.
【难度】★★★
【答案】或.
【解析】∵直线AB经过原点O和点(1,-2),
∴直线AB为正比例函数,解析式为.
设
∵△OPM的面积为, ∴,解得:
∴或.
【总结】考察面积的处理方法,注意点坐标和线段长的转换中正负号或绝对值的添法.
如图,在梯形ΑBCD中,ΑB=CD=5,ΑD=7,BC=13,E为ΑD上一定点,ΑE=4, 动点P从D出发沿着DC向C点移动,设点P移动的距离为x,ΑPE的面积为y,
求y与x的函数解析式,并画出图象.
【难度】★★★
【答案】,图像略.
【解析】分别过点A、D作AM⊥BC,DN⊥BC,垂足分别为M、N.
可得:,.
∵,, ∴,即,
∴, ∵,即,∴, ∴.
【总结】考察面积中同底等高的处理方法.
在平面直角坐标系中,函数y=2x+12的图像分别交x轴、y轴于A、B两点.过 点A的直线交y轴正半轴于点M,且点M为线段OB的中点.
求直线AM的解析式;
试在直线AM上找一点P,使得,求出点P的坐标.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵函数y=2x+12的图像分别交x轴、y轴于A、B两点,
∴,.
∵点M为线段OB的中点,
∴.
∴利用待定系数法,可得直线AM的解析式为:;
∵, ∴,∴,
即O到直线AB的距离和P到直线AB的距离相等,
∴
∴直线OP的解析式为
∵点P在直线AM上,
∴令,解得:.
∴点P的坐标为.
【总结】考察一次函数解析式的求法和同底等高的两个三角形面积相等的运用.
如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的
坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;
(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;
(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时t的值?
【难度】★★★
【答案】见解析.
【解析】(1)由题意可知,点B坐标为,
∴,
由,得:,此时P在CB上;
∵, ∴,
∴;
经分析,可知点P只能在AB或OC上.
当点P在AB边上时,设点P的坐标为,
由,得:,解得:,此时,
当点P在OC上时,设点P的坐标为,
由得:,解得:,
此时.
∴在7秒或者秒时,线段PD将梯形COAB的面积分成1:3的两部分.
【总结】本题综合性较强,主要考察勾股定理和直角梯形的性质的综合运用,注意认真分析题意.
(1)若是关于x的一次函数,则m的值?
(2)可能是正比例函数吗?可能是反比例函数吗?如果是,求出m 的值.
【难度】★
【答案】见解析.
【解析】(1)由或,∴;
当函数为正比例函数时,且,所以不可能为正比例函数;
当函数为反比例函数时,且,所以不可能是反比例函数.
【总结】考察正比例函数、反比例函数的定义.
在下列函数解析式中,属于一次函数的是( )
(1) (2)
(3) (4)
A.(1) B.(1)(3) C.(1)(2)(3) D.全部都是
【难度】★
【答案】C
【解析】形如(,为常数).
【总结】考察一次函数的定义.
如果一次函数的图像经过一、二、四象限,那么的大致图像为( ).
【难度】★
【答案】B
【解析】∵一次函数的图像经过一、二、四象限,∴,
∴经过一、三、四象限.
【总结】考察一次函数的图像及性质.
已知函数y=,点P为图象上的任意一点,过P作PA⊥x轴A,PB⊥y轴于B,则APB的面积为_______________.
【难度】★
【答案】4
【解析】矩形OAPB的面积为8,△APB的面积矩形的一半.
【总结】考察反比例函数的面积问题的处理方法.
已知y1与成正比例,y2与3x成反比例,,当x=1时,y=4,当x=-1时,y=0,求y和x的函数关系式.
【难度】★
【答案】.
【解析】∵y1与成正比例,y2与3x成反比例,
∴设,, ∴
∵当x=1时,y=4;当x=-1时,y=0, ∴, 解得:,
∴y和x的函数关系式为:.
【总结】考察正比例和反比例的概念,并且考查了复合函数解析式的确定.
若A(a1,b1),B(a2,b2)是反比例函数图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
A.b1<b2 B.b1 =b2 C.b1>b2 D.大小不确定
【难度】★★
【答案】D
【解析】反比例函数在每个象限里面随着的增大而增大.因为A、B两点不确定
在哪个象限,所以不确定纵坐标的大小关系.
【总结】考察反比例函数的增减性,注意要分象限.
如图,已知点A是一次函数y=x的图象与反比例函数的图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么AOB的面积为( )
A.2 B. C. D.
【难度】★★
【答案】C
【解析】∵点A是一次函数y=x的图象与反比例函数的图象在
第一象限内的交点,∴,∴,∴,∴
∵,∴, ∴, 故选C.
【总结】考察函数交点的求法,从而求出三角形的面积.
为了鼓励小强勤做家务,培养他的劳动意识,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费为y元,则y(元)和x(小时)之间的函数图像如图所示.
(1)根据图像,请你写出小强每月的基本生活费为多少元;父母是如何奖励小强家务劳动的?
(2)写出当0≤x≤20时,相对应的y与x之间的函数关系式;
(3)若小强5月份希望有250元费用,则小强4月份需做家务多少时间?
【难度】★★
【答案】见解析.
【解析】(1)小强每月的基本生活费为150元;如果小强每月家务劳动时间不超过20小时,
每小时奖励2.5元;如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5
元奖励,超过部分按每小时4元奖励.
设直线方程为,
∵当时,图像经过
∴, 解得:,
∴y与x之间的函数关系式为:;
(3)当时,图像经过点,
∴, 解得:, ∴
则有题意可得:, 解得:
∴当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
【总结】考察一次函数在实际问题中的运用.
现有一个种植总面积为540m2的矩形塑料温棚,分垄间隔种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物不低于10垄,又不超过14垄(垄数为整数),它们的占地面积、产量、利润分别如下:
占地面积(m2/垄) 产量(千克/垄) 利润(元/千克)
西红柿 30 160 1.1
草莓 15 50 1.6
若草莓共种植了x垄,通过计算说明共有几种种植方案?分别是哪几种?
在几种种植方案中.哪种方案获利最大?最大的利润是多少?
【难度】★★★
【答案】见解析
【解析】(1)根据题意西红柿种了垄,则,解得:
∵,且是正整数,∴,
∴共有三种种植方案:①草莓种植12垄,西红柿种植12垄;②草莓种植13垄,西红
柿种植11垄;③草莓种植14垄,西红柿种植10垄;
设种植草莓和西红柿共可获得利润元,
则
∵随着的增大而减小,∴取最小值12时,有最大值为3072元.
即草莓种植12垄,西红柿种植12垄时,有最大利润为3072元.
【总结】考察一元一次不等式与一次函数的综合应用.
在反比例函数的图像上有不重合的两点A、B,且A点的纵坐标是2,B点的横坐标是2,BB'和AA'都垂直于x轴,B',A'为垂足.(1)求A点的横坐标;
(2)求的值;(3)求的值.
【难度】★★★
【答案】(1)4;(2)4;(3)6.
【解析】(1)∵A、B两点都在反比例函数的图像上,且A点的纵坐标是2,
∴A点的横坐标是4;
(2)由题意,可得:;
(3)
.
在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线平行.
(1)求:直线l的函数解析式及点B的坐标;
(2)如直线l上有一点M(a,-6),过点M作x轴的垂线,交直线于点N,在线段MN上求一点P,使PAB是直角三角形,请求出点P的坐标.
【难度】★★★
【答案】(1),;(2)或.
【解析】(1)∵直线l与直线平行,
∴设直线l的解析式为,
∵直线l经过点A(2,-3),
∴,
∴直线l的解析式为,
∴点B的坐标为;
∵直线l上有一点M(a,-6), ∴,
则可设,
∵, ∴的取值范围是.
当AB为斜边时,
∴,
解得:,
∴点P的坐标为;
当PB为斜边时,
∴,
解得:, ∴点P的坐标为;
当PA为斜边时,,
∴,解得:,舍去
综上所述,点P的坐标为或.
【总结】考察一次函数的解析式求法和直角三角形分类讨论,本题综合性较强,注意认真分析.
同课章节目录
