宁夏银川市第一高级中学校2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 宁夏银川市第一高级中学校2020-2021学年高一上学期期末考试数学试题 Word版含答案 | 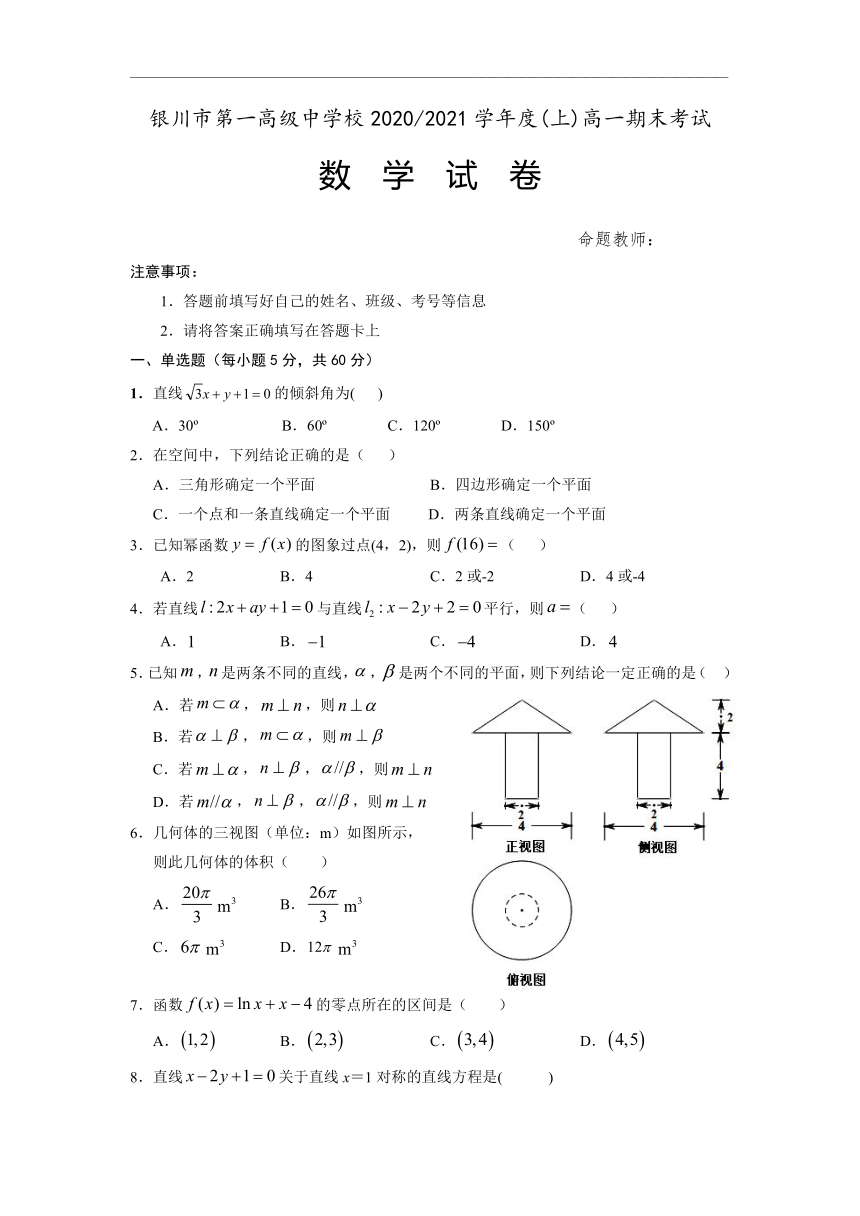 | |
| 格式 | doc | ||
| 文件大小 | 837.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 22:05:34 | ||
图片预览




文档简介
____________________________________________________________________________________________
银川市第一高级中学校2020/2021学年度(上)高一期末考试
数 学 试 卷
命题教师:
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题5分,共60分)
1.直线的倾斜角为(? ? )
A.30? B.60? C.120? D.150?
2.在空间中,下列结论正确的是( )
A.三角形确定一个平面 B.四边形确定一个平面
C.一个点和一条直线确定一个平面 D.两条直线确定一个平面
3.已知幂函数的图象过点(4,2),则( )
A.2 B.4 C.2或-2 D.4或-4
4.若直线与直线平行,则( )
A. B. C. D.
5.已知,是两条不同的直线,,是两个不同的平面,则下列结论一定正确的是( )
A.若,,则
B.若,,则
C.若,,,则
D.若,,,则
6.几何体的三视图(单位:m)如图所示,
则此几何体的体积( )
A. B.
C. D.
7.函数的零点所在的区间是( )
A. B. C. D.
8.直线关于直线x=1对称的直线方程是( )
A. B.
C. D.
9.直线被圆截得的弦长等于( )
A.4 B.2 C. D.
10.如图,正方体ABCD-A1B1C1D1的棱长为2,下面结论错误的是( )
A.BD∥平面CB1D1
B.AC1⊥平面CB1D1
C.异面直线CB1与BD所成角为60°
D.三棱锥D-CB1D1体积为
11.是直线上的动点,直线,分别与圆相切于,
两点,则四边形(为坐标原点)的面积的最小值等于( )
A.8 B.4 C.24 D.16
12.已知函数,关于的方程有 个不相等的实数根,则的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
13.与圆()相内切,则_________.
14.若球的表面积为,有一平面与球心的距离为1,则球被该平面截得的圆的面积为 .
15.函数的零点个数为 个.
16.如图,已知四棱锥的底面为等腰梯形,,
,,且平面,
则四棱锥外接球的体积为 .
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知的顶点坐标分别为
(1)求直线的方程;
(2)求边上的高所在的直线方程.
18.(12分)
如图,在三棱锥中,平面,
底面是直角三角形,,是
棱的中点,是的重心,是的中点.
(1)求证:平面;
(2)求证:;
19.(12分)
2020年初的新冠疫情危害人民生命健康的同时也严重阻碍了经济的发展,英雄的中国人民率先战胜了疫情,重启了经济引擎.今年夏天武汉某大学毕业生创建了一个生产电子仪器的小公司.该公司生产一种电子仪器每月的固定成本为20000元(如房租、水电等成本),每生产一台仪器需增加投入80元,已知每月生产台的总收益满足函数,其中是仪器的月产量.
(1)写出月利润关于月产量的函数解析式;(总收益=总成本+利润)
(2)当月产量为何值时,公司每月所获得利润最大?最大利润为多少元?
20.(12分)
在平行四边形中,,,过A点作的垂线交的延长线于点E,.连结交于点F,如图1,将△沿折起,使得点E到达点P的位置.如图2.
(1)证明:;
(2)若G为的中点,H为的中点,且平面平面,求三棱锥的体积.
21.(12分)
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,过AB的截面与上底面交于PQ,且点P在棱A1D1上,点Q在棱C1B1上,且AB=1,AC=,BC=2.
(1)求证:;
(2)若二面角A-C1D-C的平面角的余弦值为,
求侧棱BB1的长.
22.(12分)
圆.
(1)若圆与轴相切,求圆的方程;
(2)已知,圆与轴相交于两点M,N (点M在点N的左侧)。过点M任作一条与轴不重合的直线与圆相交于两点A,B。是否存在实数,使得?若存在,求出实数的值,若不存在,请说明理由.
高一期末考试试卷答案
选择题
1 2 3 4 5 6 7 8 9 10 11 12
C A B C D A B D A D A D
填空题
1 ; 14. ; 15. 2 ; 16 .
解答题
(1);(2)
(1)中,,,
由两点间斜率公式可得,…………………………2分
所以直线的方程为,
即.……………………………………5分
(2)设边上的高所在的直线为,
则由垂直直线的斜率乘积为可得……………………2分
所以的直线方程为,
∴边上的高所在的直线方程为:.………………5分
18.
(1)证明:
……………………6分
(2)证明:连结并延长交于点,连结,…………1分
是的重心, 为边上的中线, 为边上的中点,
又有为边上的中点, ,……………………2分
同理可得……………………………………3分
且
,…………………………4分
又有
………………………………………………6分
19.
解:(1)月产量为台,则总成本为20 000+80………………2分
那么, ………………6分
(2)当时,,
所以当时,最大值为60000;…………………………2分
当时,是减函数,且,…………4分
所以当时,函数的最大值为60000,即当月产量为400台时,所获得利润最大,
最大利润为60000元.……………………6分
20.
(Ⅰ)证明:如图1,在中,,,所以.所以
∵△ADE也是直角三角形,
,,
,,………………………2分
如图2,,…………………………4分
,
从而平面,又平面,所以.………………………6分
(Ⅱ)平面平面,且平面平面,
平面,,平面.……………………2分
G为的中点,三棱锥的高等于.……………3分
H为的中点,∴△BCH的面积是四边形的面积的,…………4分
三棱锥的体积是四棱锥的体积的.
,
三棱锥的体积为.……………………6分
21.
PQ//AB…………………………4分
AB//A1B1
………………………………6分
(1)证明:∵在底面ABCD中,AB=1,AC=,BC=2,
∴AB2+AC2=BC2,∴AB⊥AC,
∵侧棱AA1⊥底面ABCD,AC?平面ABCD,
∴AA1⊥AC,
又∵AA1∩AB=A,AA1,AB?平面ABB1A1,
∴AC⊥平面ABB1A1.
过点C作CP⊥C1D于P,连接AP
∠CPA是二面角A-C1D-C的平面角………………4分
∵cos,tan,CD=AB=1,
∴CP=,
设BB1∴,
?解得…………………………6分
22.
(1)由圆与轴相切,可知圆心的横坐标的绝对值与半径与相等.故先将圆的方程化成标准方程为:,…………2分
∵恒成立,∴求得或,
即可得到所求圆的方程为:或;…………5分
(2)令,得,即所以,……1分
假设存在实数,当直线与轴不垂直时,设直线的方程为,
代入得,,……2分
设,从而,,…………3分
因为,所以…………5分
因为
而
即,得.…………6分
当直线与轴垂直时,也成立.
故存在,使得.…………7分
银川市第一高级中学校2020/2021学年度(上)高一期末考试
数 学 试 卷
命题教师:
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题5分,共60分)
1.直线的倾斜角为(? ? )
A.30? B.60? C.120? D.150?
2.在空间中,下列结论正确的是( )
A.三角形确定一个平面 B.四边形确定一个平面
C.一个点和一条直线确定一个平面 D.两条直线确定一个平面
3.已知幂函数的图象过点(4,2),则( )
A.2 B.4 C.2或-2 D.4或-4
4.若直线与直线平行,则( )
A. B. C. D.
5.已知,是两条不同的直线,,是两个不同的平面,则下列结论一定正确的是( )
A.若,,则
B.若,,则
C.若,,,则
D.若,,,则
6.几何体的三视图(单位:m)如图所示,
则此几何体的体积( )
A. B.
C. D.
7.函数的零点所在的区间是( )
A. B. C. D.
8.直线关于直线x=1对称的直线方程是( )
A. B.
C. D.
9.直线被圆截得的弦长等于( )
A.4 B.2 C. D.
10.如图,正方体ABCD-A1B1C1D1的棱长为2,下面结论错误的是( )
A.BD∥平面CB1D1
B.AC1⊥平面CB1D1
C.异面直线CB1与BD所成角为60°
D.三棱锥D-CB1D1体积为
11.是直线上的动点,直线,分别与圆相切于,
两点,则四边形(为坐标原点)的面积的最小值等于( )
A.8 B.4 C.24 D.16
12.已知函数,关于的方程有 个不相等的实数根,则的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
13.与圆()相内切,则_________.
14.若球的表面积为,有一平面与球心的距离为1,则球被该平面截得的圆的面积为 .
15.函数的零点个数为 个.
16.如图,已知四棱锥的底面为等腰梯形,,
,,且平面,
则四棱锥外接球的体积为 .
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知的顶点坐标分别为
(1)求直线的方程;
(2)求边上的高所在的直线方程.
18.(12分)
如图,在三棱锥中,平面,
底面是直角三角形,,是
棱的中点,是的重心,是的中点.
(1)求证:平面;
(2)求证:;
19.(12分)
2020年初的新冠疫情危害人民生命健康的同时也严重阻碍了经济的发展,英雄的中国人民率先战胜了疫情,重启了经济引擎.今年夏天武汉某大学毕业生创建了一个生产电子仪器的小公司.该公司生产一种电子仪器每月的固定成本为20000元(如房租、水电等成本),每生产一台仪器需增加投入80元,已知每月生产台的总收益满足函数,其中是仪器的月产量.
(1)写出月利润关于月产量的函数解析式;(总收益=总成本+利润)
(2)当月产量为何值时,公司每月所获得利润最大?最大利润为多少元?
20.(12分)
在平行四边形中,,,过A点作的垂线交的延长线于点E,.连结交于点F,如图1,将△沿折起,使得点E到达点P的位置.如图2.
(1)证明:;
(2)若G为的中点,H为的中点,且平面平面,求三棱锥的体积.
21.(12分)
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,过AB的截面与上底面交于PQ,且点P在棱A1D1上,点Q在棱C1B1上,且AB=1,AC=,BC=2.
(1)求证:;
(2)若二面角A-C1D-C的平面角的余弦值为,
求侧棱BB1的长.
22.(12分)
圆.
(1)若圆与轴相切,求圆的方程;
(2)已知,圆与轴相交于两点M,N (点M在点N的左侧)。过点M任作一条与轴不重合的直线与圆相交于两点A,B。是否存在实数,使得?若存在,求出实数的值,若不存在,请说明理由.
高一期末考试试卷答案
选择题
1 2 3 4 5 6 7 8 9 10 11 12
C A B C D A B D A D A D
填空题
1 ; 14. ; 15. 2 ; 16 .
解答题
(1);(2)
(1)中,,,
由两点间斜率公式可得,…………………………2分
所以直线的方程为,
即.……………………………………5分
(2)设边上的高所在的直线为,
则由垂直直线的斜率乘积为可得……………………2分
所以的直线方程为,
∴边上的高所在的直线方程为:.………………5分
18.
(1)证明:
……………………6分
(2)证明:连结并延长交于点,连结,…………1分
是的重心, 为边上的中线, 为边上的中点,
又有为边上的中点, ,……………………2分
同理可得……………………………………3分
且
,…………………………4分
又有
………………………………………………6分
19.
解:(1)月产量为台,则总成本为20 000+80………………2分
那么, ………………6分
(2)当时,,
所以当时,最大值为60000;…………………………2分
当时,是减函数,且,…………4分
所以当时,函数的最大值为60000,即当月产量为400台时,所获得利润最大,
最大利润为60000元.……………………6分
20.
(Ⅰ)证明:如图1,在中,,,所以.所以
∵△ADE也是直角三角形,
,,
,,………………………2分
如图2,,…………………………4分
,
从而平面,又平面,所以.………………………6分
(Ⅱ)平面平面,且平面平面,
平面,,平面.……………………2分
G为的中点,三棱锥的高等于.……………3分
H为的中点,∴△BCH的面积是四边形的面积的,…………4分
三棱锥的体积是四棱锥的体积的.
,
三棱锥的体积为.……………………6分
21.
PQ//AB…………………………4分
AB//A1B1
………………………………6分
(1)证明:∵在底面ABCD中,AB=1,AC=,BC=2,
∴AB2+AC2=BC2,∴AB⊥AC,
∵侧棱AA1⊥底面ABCD,AC?平面ABCD,
∴AA1⊥AC,
又∵AA1∩AB=A,AA1,AB?平面ABB1A1,
∴AC⊥平面ABB1A1.
过点C作CP⊥C1D于P,连接AP
∠CPA是二面角A-C1D-C的平面角………………4分
∵cos,tan,CD=AB=1,
∴CP=,
设BB1∴,
?解得…………………………6分
22.
(1)由圆与轴相切,可知圆心的横坐标的绝对值与半径与相等.故先将圆的方程化成标准方程为:,…………2分
∵恒成立,∴求得或,
即可得到所求圆的方程为:或;…………5分
(2)令,得,即所以,……1分
假设存在实数,当直线与轴不垂直时,设直线的方程为,
代入得,,……2分
设,从而,,…………3分
因为,所以…………5分
因为
而
即,得.…………6分
当直线与轴垂直时,也成立.
故存在,使得.…………7分
同课章节目录
