8.3 实际问题与二元一次方程组
文档属性
| 名称 | 8.3 实际问题与二元一次方程组 |

|
|
| 格式 | zip | ||
| 文件大小 | 27.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-05 00:00:00 | ||
图片预览

文档简介
8.3实际问题与二元一次方程组
教学任务分析
教学目标 知识技能 使学生能够探索事物之间的数量关系,利用方程或方程组解决实际问题.
数学思考 通过问题探究,使学生进一步使用代数中的方程来反映现实世界的等量关系,体会代数方法的优越性.
解决问题 使学生能够根据实际问题,寻找其中的相等关系,最终转化为数学问题求解.
情感态度 进一步培养学生化实际问题为数学问题的能力,培养严谨慎密的科学习惯,继续渗透转化的数学思想.
重点 能够根据题意找出相等关系,根据相等关系列出方程或方程组解决实际问题.
难点 准确找到实际问题中的相等关系,解释结果的合理性.
教学流程安排
活动流程图 活动内容和目的
探究1 养牛场问题探究2 种植面积问题探究3 运输问题 小结与作业 创设问题情境,激发学生兴趣,引起探索渴望.主体探索,合作交流,培养学生分析、解决问题的能力,锻炼学生思维的灵活性和深刻性.问题解决,在交流解法的过程中培养学生的语言表述能力以及交流能力.复习巩固、归纳总结.
教学过程设计
创设问题情境,激发学生兴趣,引起探索渴望.
探究1:养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940 kg.饲养员李大叔估计平均每只大牛1天约需要饲料18~20 kg,每只小牛1天约需要7~8 kg.你能否通过计算检验他的估计?
探究2:根据以往的统计资料,甲、乙两种作物的单位面积的产量比是1∶1.5,现在要在一块长为200 m,宽100 m的长方形的土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量比为3∶4(结果取整数)?
图1
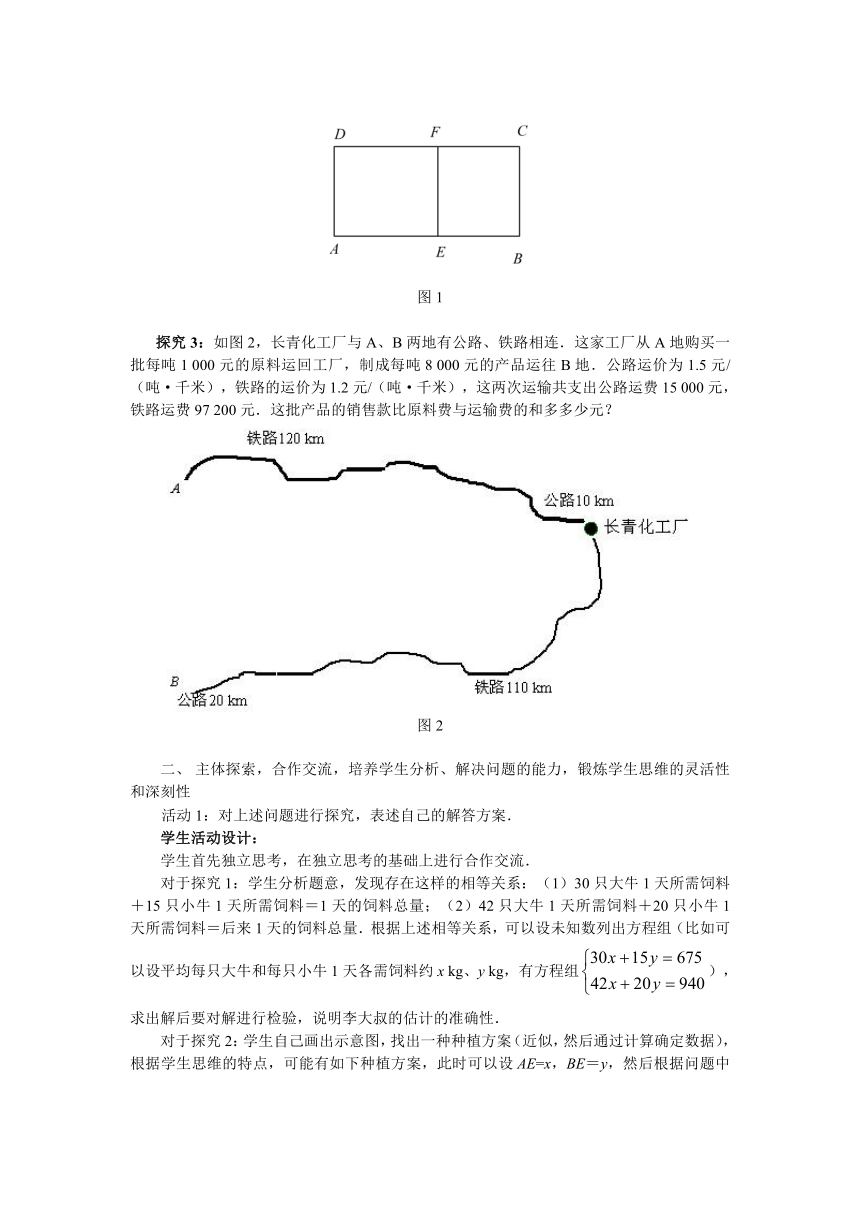
探究3:如图2,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B地.公路运价为1.5元/(吨·千米),铁路的运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
图2
主体探索,合作交流,培养学生分析、解决问题的能力,锻炼学生思维的灵活性和深刻性
活动1:对上述问题进行探究,表述自己的解答方案.
学生活动设计:
学生首先独立思考,在独立思考的基础上进行合作交流.
对于探究1:学生分析题意,发现存在这样的相等关系:(1)30只大牛1天所需饲料+15只小牛1天所需饲料=1天的饲料总量;(2)42只大牛1天所需饲料+20只小牛1天所需饲料=后来1天的饲料总量.根据上述相等关系,可以设未知数列出方程组(比如可以设平均每只大牛和每只小牛1天各需饲料约x kg、y kg,有方程组),求出解后要对解进行检验,说明李大叔的估计的准确性.
对于探究2:学生自己画出示意图,找出一种种植方案(近似,然后通过计算确定数据),根据学生思维的特点,可能有如下种植方案,此时可以设AE=x,BE=y,然后根据问题中的产量、长度找到相等关系,列出方程组,解出方程组的解后解释具体方案.
对于探究3:学生经过分析可以发现其中的数量关系有,(1)两段公路费共有15 000元;(2)两段铁路总费用是97 200元,销售款与产品数量有关,原料费与原料数量有关,可以设产品重x吨,原料重y吨,于是从A到化工厂铁路费是120y×1.2、公路费用是10y×1.5元;从化工厂到B地的铁路费是110x×1.2、公路费用是20x×1.5元.
于是有方程组,解出结果后,进行检验,进一步计算这批产品的销售款比原料费与运输费的和多多少元.
教师活动设计:
本节课的主要目的,是使学生在探究如何用方程组解决实际问题的过程中,进一步提高分析问题中的数量关系、设未知数、列方程组并解方程组、检验结果的合理性的能力,同时这些问题要比以前的问题更接近现实,因此分析、解决的难度也要大一些.对于这些问题不能像对待前面的例题一样,应充分发挥学生的自主学习的积极性,引导学生先独立探究,再进行合作交流.
探究1是有关牛饲料的问题,学生分析解决问题后要对李大叔的估计作出判断,从而要求进行精确计算.
探究2是一个开放性的问题,其解决方法不止一种,通过此问题的解决,让学生体会一题多解的问题情境,学习从多角度考虑问题;分析这个问题,提醒学生注意:
(1)要把这个长方形分成两个长方形;
(2)两块地分别种甲、乙两种作物,它们的产量比是3:4.
首先可以考虑前一个要求,容易想到划分的方法是沿这块土地的边的方向画线.在此基础上考虑另一要求,这就与长方形面积以及两种作物的产量比有关了.(注意此时得到的答案不是整数值,为了符合要求需要取近似值.)
探究3索要的答案是一个值,但是直接设这个值为未知数列方程不太容易.为此可以引导学生设间接的未知数,即先设产品数量和原料数量分别为x、y,解出它们后再计算问题索要的答案.另外在探究3的解决过程中,注意培养学生从图表中获取信息的能力.
最后引导学生归纳:
方程组是解决含有多个未知数问题的重要工具,列出方程组要根据问题中的数量关系,得出方程组的解后要进一步考虑它是否符合问题的实际意义.
三、问题解决,在交流解法的过程中培养学生的语言表述能力以及交流能力.
〔解答〕
探究1:设平均每只大牛和每只小牛各需饲料约x kg、y kg,则
,
解得
.
因此饲养员李大叔对大牛的食量估计较为准确,而对小牛的食量的估计偏高.
探究2:如图这种种植方案,设AE=x,BE=y,则
,
解得
,
由于结果要取整数,
可以确定这种种植方案是:过长方形土地的长边上离一端约为106米处,把这个长方形分为两个长方形.较大的一块种甲种农作物,较小的一块种乙种农作物.
探究3:设产品重x吨,原料重y吨,则
,
解得,进而计算得到这批产品的销售款比原料费与运输费的和多1 887 800元.
四、归纳小结、布置作业.
小结:本节你遇到了哪些问题?你是怎样解决的?
作业:
1.已经进入汛期,七年级二班的同学们到水库调查了解汛情.水库一共有10个泄洪闸,现在水库的水位已经超过安全线,上游的河水仍以一个不变的速度流入水库.同学们经过一天的观察和测量,做了如下记录:上午打开一个泄洪闸,在2小时内水位继续上升了0.06米;下午再打开2个泄洪闸后,4小时水位下降了0.1米.目前水位仍超过安全线1.2米.
(1)如果打开5个泄洪闸,还需几小时水位降到安全线?
(2)如果防汛指挥部要求6小时内使水位降到安全线,至少应该打开几个泄洪闸?
〔解答〕
设河水的流入使水位上升x米/时,每个闸门泄洪可以使水位下降y米/时,则有
,解得.
(1)设打开5个泄洪闸,需t小时水位降到安全线,则有
0.0575t-0.0275×5 t=-1.2,t=15时.
(2)设打开n个闸门,需要6小时水位降到安全线,则有
6×0.0575-6×0.0275n=-1.2,n≈9.36,因此应打开10个闸门.
2.习题 8.3.
教学任务分析
教学目标 知识技能 使学生能够探索事物之间的数量关系,利用方程或方程组解决实际问题.
数学思考 通过问题探究,使学生进一步使用代数中的方程来反映现实世界的等量关系,体会代数方法的优越性.
解决问题 使学生能够根据实际问题,寻找其中的相等关系,最终转化为数学问题求解.
情感态度 进一步培养学生化实际问题为数学问题的能力,培养严谨慎密的科学习惯,继续渗透转化的数学思想.
重点 能够根据题意找出相等关系,根据相等关系列出方程或方程组解决实际问题.
难点 准确找到实际问题中的相等关系,解释结果的合理性.
教学流程安排
活动流程图 活动内容和目的
探究1 养牛场问题探究2 种植面积问题探究3 运输问题 小结与作业 创设问题情境,激发学生兴趣,引起探索渴望.主体探索,合作交流,培养学生分析、解决问题的能力,锻炼学生思维的灵活性和深刻性.问题解决,在交流解法的过程中培养学生的语言表述能力以及交流能力.复习巩固、归纳总结.
教学过程设计
创设问题情境,激发学生兴趣,引起探索渴望.
探究1:养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940 kg.饲养员李大叔估计平均每只大牛1天约需要饲料18~20 kg,每只小牛1天约需要7~8 kg.你能否通过计算检验他的估计?
探究2:根据以往的统计资料,甲、乙两种作物的单位面积的产量比是1∶1.5,现在要在一块长为200 m,宽100 m的长方形的土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量比为3∶4(结果取整数)?
图1
探究3:如图2,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B地.公路运价为1.5元/(吨·千米),铁路的运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
图2
主体探索,合作交流,培养学生分析、解决问题的能力,锻炼学生思维的灵活性和深刻性
活动1:对上述问题进行探究,表述自己的解答方案.
学生活动设计:
学生首先独立思考,在独立思考的基础上进行合作交流.
对于探究1:学生分析题意,发现存在这样的相等关系:(1)30只大牛1天所需饲料+15只小牛1天所需饲料=1天的饲料总量;(2)42只大牛1天所需饲料+20只小牛1天所需饲料=后来1天的饲料总量.根据上述相等关系,可以设未知数列出方程组(比如可以设平均每只大牛和每只小牛1天各需饲料约x kg、y kg,有方程组),求出解后要对解进行检验,说明李大叔的估计的准确性.
对于探究2:学生自己画出示意图,找出一种种植方案(近似,然后通过计算确定数据),根据学生思维的特点,可能有如下种植方案,此时可以设AE=x,BE=y,然后根据问题中的产量、长度找到相等关系,列出方程组,解出方程组的解后解释具体方案.
对于探究3:学生经过分析可以发现其中的数量关系有,(1)两段公路费共有15 000元;(2)两段铁路总费用是97 200元,销售款与产品数量有关,原料费与原料数量有关,可以设产品重x吨,原料重y吨,于是从A到化工厂铁路费是120y×1.2、公路费用是10y×1.5元;从化工厂到B地的铁路费是110x×1.2、公路费用是20x×1.5元.
于是有方程组,解出结果后,进行检验,进一步计算这批产品的销售款比原料费与运输费的和多多少元.
教师活动设计:
本节课的主要目的,是使学生在探究如何用方程组解决实际问题的过程中,进一步提高分析问题中的数量关系、设未知数、列方程组并解方程组、检验结果的合理性的能力,同时这些问题要比以前的问题更接近现实,因此分析、解决的难度也要大一些.对于这些问题不能像对待前面的例题一样,应充分发挥学生的自主学习的积极性,引导学生先独立探究,再进行合作交流.
探究1是有关牛饲料的问题,学生分析解决问题后要对李大叔的估计作出判断,从而要求进行精确计算.
探究2是一个开放性的问题,其解决方法不止一种,通过此问题的解决,让学生体会一题多解的问题情境,学习从多角度考虑问题;分析这个问题,提醒学生注意:
(1)要把这个长方形分成两个长方形;
(2)两块地分别种甲、乙两种作物,它们的产量比是3:4.
首先可以考虑前一个要求,容易想到划分的方法是沿这块土地的边的方向画线.在此基础上考虑另一要求,这就与长方形面积以及两种作物的产量比有关了.(注意此时得到的答案不是整数值,为了符合要求需要取近似值.)
探究3索要的答案是一个值,但是直接设这个值为未知数列方程不太容易.为此可以引导学生设间接的未知数,即先设产品数量和原料数量分别为x、y,解出它们后再计算问题索要的答案.另外在探究3的解决过程中,注意培养学生从图表中获取信息的能力.
最后引导学生归纳:
方程组是解决含有多个未知数问题的重要工具,列出方程组要根据问题中的数量关系,得出方程组的解后要进一步考虑它是否符合问题的实际意义.
三、问题解决,在交流解法的过程中培养学生的语言表述能力以及交流能力.
〔解答〕
探究1:设平均每只大牛和每只小牛各需饲料约x kg、y kg,则
,
解得
.
因此饲养员李大叔对大牛的食量估计较为准确,而对小牛的食量的估计偏高.
探究2:如图这种种植方案,设AE=x,BE=y,则
,
解得
,
由于结果要取整数,
可以确定这种种植方案是:过长方形土地的长边上离一端约为106米处,把这个长方形分为两个长方形.较大的一块种甲种农作物,较小的一块种乙种农作物.
探究3:设产品重x吨,原料重y吨,则
,
解得,进而计算得到这批产品的销售款比原料费与运输费的和多1 887 800元.
四、归纳小结、布置作业.
小结:本节你遇到了哪些问题?你是怎样解决的?
作业:
1.已经进入汛期,七年级二班的同学们到水库调查了解汛情.水库一共有10个泄洪闸,现在水库的水位已经超过安全线,上游的河水仍以一个不变的速度流入水库.同学们经过一天的观察和测量,做了如下记录:上午打开一个泄洪闸,在2小时内水位继续上升了0.06米;下午再打开2个泄洪闸后,4小时水位下降了0.1米.目前水位仍超过安全线1.2米.
(1)如果打开5个泄洪闸,还需几小时水位降到安全线?
(2)如果防汛指挥部要求6小时内使水位降到安全线,至少应该打开几个泄洪闸?
〔解答〕
设河水的流入使水位上升x米/时,每个闸门泄洪可以使水位下降y米/时,则有
,解得.
(1)设打开5个泄洪闸,需t小时水位降到安全线,则有
0.0575t-0.0275×5 t=-1.2,t=15时.
(2)设打开n个闸门,需要6小时水位降到安全线,则有
6×0.0575-6×0.0275n=-1.2,n≈9.36,因此应打开10个闸门.
2.习题 8.3.
