2020年人教版七年级下册5.3平行线的性质学案(Word版附课堂练习课后练习无答案)
文档属性
| 名称 | 2020年人教版七年级下册5.3平行线的性质学案(Word版附课堂练习课后练习无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 769.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 00:00:00 | ||
图片预览




文档简介
平行线性质
知识点一:平行线性质
()性质:两条平行直线被第三条直线所截,同位角相等.简称为:两直线平行,_同位角_相等.如图所示,用符号表示为:因为,所以.
()性质:两条平行直线被第三条直线所截,内错角相等.简称为:两直线平行,内错角相等.如图所示,用符号表示为:因为,所以.
()性质:两条平行直线被第三条直线所截,同旁内角互补.简称为:两直线平行,同旁内角互补.如图所示,用符号表示为:因为,所以.
注意:(1)同位角相等、内错角相等和同旁内角互补是由平行线的性质所得的结论,所以它们成立的前提是“两直线平行”.
(2)要注意正确区分平行线的性质与判定,由角的数量关系得到两条直线平行,是平行线的判定;由两条直线平行得到角的数量关系,是平行线的性质.
(3)要特别注意没有两条直线平行这个条件,同位角和内错角不相等,同旁内角也不互补.
例1:如图,平分,点在上,,若,则的度数为(
).
A.
B.
C.
D.
例2:如图,小明在操场上从点出发,先沿南偏东方向走到点,再沿南偏东方向走到点,这时的度数是(
).
A.
B.
C.
D.
例3:如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为(
)
A.65°
B.55°
C.45°
D.35°
课堂练习:
1、如图,直线,,,那么的度数为(
).
A.
B.
C.
D.
2、如图,已知,,则__________.
3、如图,一个含有角的直角三角尺的两个顶点放在一个长方形的对边上,如果,那么的度数是__________度.
4、如图,,,,求的度数.
5、如图,已知,,,则等于(
).
A.
B.
C.
D.
6、如图,已知,直角三角尺的直角顶点在直线上,若,则下列结论错误的是(
)
A.
B.
C.
D.
7、如图,,平分交于点,若,则(
).
A.
B.
C.
D.
8、如图所示,直线,与直线,相交,已知,,则(
).
A.
B.
C.
D.
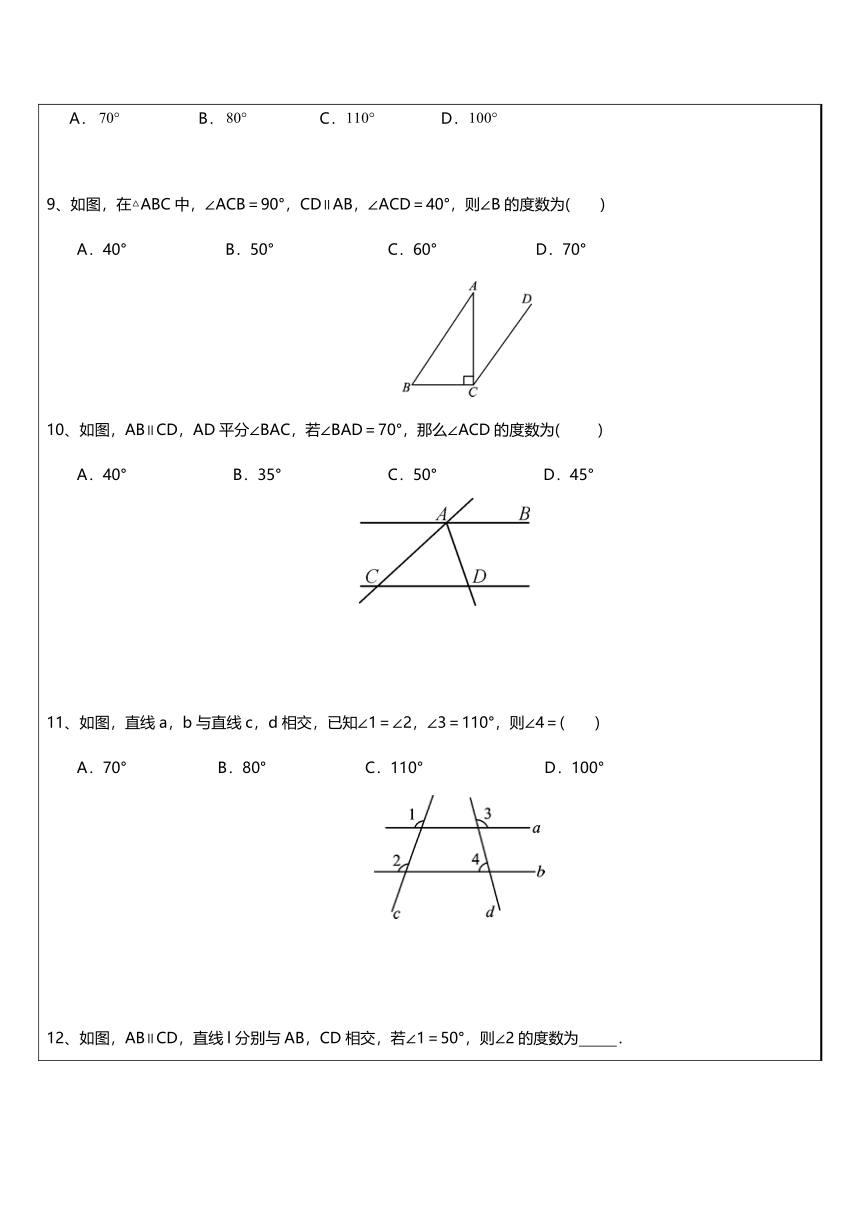
9、如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为(
)
A.40°
B.50°
C.60°
D.70°
10、如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为(
)
A.40°
B.35°
C.50°
D.45°
11、如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=(
)
A.70°
B.80°
C.110°
D.100°
12、如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为
.
13、如图,直线a,b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是
.
知识点二:平行线性质与判定的综合应用
1.平行线的判定与性质的比较
平行线的判定平行线的性质同位角角相等,两直线平行两直线平行,同位角相等内错角相等,两直线平行两直线平行,内错角相等同旁内角互补,两直线平行两直线平移地,同旁内角互补由角的“数量关系”决定线的“位置关系”由线的“位置关系”决定角的“数量关系”
例1:如图,,,,则的度数为(
).
A.
B.
C.
D.
例2:如图所示,在三角形中,,,,则的度数为(
).
A.
B.
C.
D.
课堂练习:
1、如图,,,若,则的度数为(
).
A.
B.
C.
D.
2、如图,直线,是的平分线,,则的度数是(
).
A.
B.
C.
D.
3、如图,,直线与,分别交于点,,过点的直线与
交于点,则下列结论错误的是(
).
A.
B.
C.
D.
4、如图,直线,平分,若,则__________.
5、如图,,若,,则__________.
6、如图,,交于点,于点,若__________.
7、如图,已知,.若,,则的度数是__________.
8、如图,已知,,则下列结论不成立的是(
).
A.
B.
C.
D.
9、图中,,均是平行线,被直线所截得到的角,其中相等的两个角有(
)对.
A.
B.
C.
D.
10、如图,已知,,,四条直线,,,,则等于(
).
A.
B.
C.
D.
11、如图,直线,,,则__________.
12、如图,,,交的平分线于点,
,则__________.
13、将一副三角尺拼成如图所示的图形,过点作平分,交于点.
()试说明:.
()求的度数.
知识点二:平行线性质的应用
一、平行线与三角形
例1:如图,直线,,,则等于(
).
A.
B.
C.
D.
练习:
1、如图,直线,,,则的度数是(
).
A.
B.
C.
D.
2、如图,直线,,,则的度数是(
).
A.
B.
C.
D.
3、如图,直线,若,,则等于(
).
A.
B.
C.
D.
二、平行线与角平分线
例1:如图,,平分,,则等于(
).
A.
B.
C.
D.
练习:
1、如图,已知,平分,,则为(
).
A.
B.
C.
D.
2、如图,直线,平分,与相交于点,,则
的度数是(
).
A.
B.
C.
D.
3、将一张长方形纸片折叠成如图所示的形状,则(
).
A.
B.
C.
D.
.
三、平行线与垂线
例1:如图①,于点,,,则等于(
).
A.
B.
C.
D.
例2:如图②,直线,于点,,则的度数为(
).
A.
B.
C.
D.
练习:
1、如图,直线,点在直线上,且,,那么的度数是(
).
A.
B.
C.
D.
2、如图,,,垂足为,若,则的度数为(
).
A.
B.
C.
D.
四、平行线与辅助线
例1:如图①,已知,,,则的度数为(
).
A.
B.
C.
D.
例2:如图②,,于点,若,则(
).
A.
B.
C.
D.
例3:如图,直线,若,,则(
).
A.
B.
C.
D.
练习:
如图,的一边为平面镜,,在上有一点,从点射出一束光线经上一点反射,反射光线恰好与平行,则的度数是(
).
A.
B.
C.
D.
2、如图①是我们常用的折叠式小刀,图②中刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图②所示的与,则与的度数和是__________度.
五、平行线与三角尺
例1:小红把一把直尺与一块三角尺如图放置,测得.则的度数为(
).
A.
B.
C.
D.
练习:
1、如图,在平行线,之间放置一块直角三角尺,三角尺的顶点,分别在直线,上,则的值为(
).
A.
B.
C.
D.
2、将一副直角三角尺如图放置,使含角的三角尺的直角边和含角的三角尺的一条直角边在同一条直线上,则的度数为(
).
A.
B.
C.
D.
3、如图,将一副三角尺叠放在一起,使直角的顶点重合于点,,与交于点,则的度数为(
).
A.
B.
C.
D.
4.如图,将一块含有角的直角三角尺的两个顶点放在两条平行的直线,上,如果,那么的度数为(
).
A.
B.
C.
D.
5、如图,将一副三角尺和一张对边平行的纸条按下列方式摆放,两个三角尺的一直角边重合,含角的直角三角尺的斜边与纸条一边重合,含角的三角尺的一个顶点在纸条的另一边上,则的度数是__________.
课堂练习:
1、某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是(
)
A.30°
B.45°
C.60°
D.75°
2、一只因损坏而倾斜的椅子,从背后看到的形状如图所示,其中两组对边的平行关系没有发生变化,若∠1=76°,则∠2的大小是(
)
A.76°
B.86°
C.104°
D.114°
3、如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为(D)
A.60°
B.65°
C.70°
D.75°
4、如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是(
)
A.∠EMB=∠END
B.∠BMN=∠MNC
C.∠CNH=∠BPG
D.∠DNG=∠AME
5、如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(
)
A.60°
B.120°
C.150°
D.180°
6、一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=
°.
7、如图,一只船从点A出发沿北偏东60°方向航行到点B,再以南偏西25°方向返回,则∠ABC=
°.
8、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
9、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
10、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东
°.
11、某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
知识点一:平行线性质
()性质:两条平行直线被第三条直线所截,同位角相等.简称为:两直线平行,_同位角_相等.如图所示,用符号表示为:因为,所以.
()性质:两条平行直线被第三条直线所截,内错角相等.简称为:两直线平行,内错角相等.如图所示,用符号表示为:因为,所以.
()性质:两条平行直线被第三条直线所截,同旁内角互补.简称为:两直线平行,同旁内角互补.如图所示,用符号表示为:因为,所以.
注意:(1)同位角相等、内错角相等和同旁内角互补是由平行线的性质所得的结论,所以它们成立的前提是“两直线平行”.
(2)要注意正确区分平行线的性质与判定,由角的数量关系得到两条直线平行,是平行线的判定;由两条直线平行得到角的数量关系,是平行线的性质.
(3)要特别注意没有两条直线平行这个条件,同位角和内错角不相等,同旁内角也不互补.
例1:如图,平分,点在上,,若,则的度数为(
).
A.
B.
C.
D.
例2:如图,小明在操场上从点出发,先沿南偏东方向走到点,再沿南偏东方向走到点,这时的度数是(
).
A.
B.
C.
D.
例3:如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为(
)
A.65°
B.55°
C.45°
D.35°
课堂练习:
1、如图,直线,,,那么的度数为(
).
A.
B.
C.
D.
2、如图,已知,,则__________.
3、如图,一个含有角的直角三角尺的两个顶点放在一个长方形的对边上,如果,那么的度数是__________度.
4、如图,,,,求的度数.
5、如图,已知,,,则等于(
).
A.
B.
C.
D.
6、如图,已知,直角三角尺的直角顶点在直线上,若,则下列结论错误的是(
)
A.
B.
C.
D.
7、如图,,平分交于点,若,则(
).
A.
B.
C.
D.
8、如图所示,直线,与直线,相交,已知,,则(
).
A.
B.
C.
D.
9、如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为(
)
A.40°
B.50°
C.60°
D.70°
10、如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为(
)
A.40°
B.35°
C.50°
D.45°
11、如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=(
)
A.70°
B.80°
C.110°
D.100°
12、如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为
.
13、如图,直线a,b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是
.
知识点二:平行线性质与判定的综合应用
1.平行线的判定与性质的比较
平行线的判定平行线的性质同位角角相等,两直线平行两直线平行,同位角相等内错角相等,两直线平行两直线平行,内错角相等同旁内角互补,两直线平行两直线平移地,同旁内角互补由角的“数量关系”决定线的“位置关系”由线的“位置关系”决定角的“数量关系”
例1:如图,,,,则的度数为(
).
A.
B.
C.
D.
例2:如图所示,在三角形中,,,,则的度数为(
).
A.
B.
C.
D.
课堂练习:
1、如图,,,若,则的度数为(
).
A.
B.
C.
D.
2、如图,直线,是的平分线,,则的度数是(
).
A.
B.
C.
D.
3、如图,,直线与,分别交于点,,过点的直线与
交于点,则下列结论错误的是(
).
A.
B.
C.
D.
4、如图,直线,平分,若,则__________.
5、如图,,若,,则__________.
6、如图,,交于点,于点,若__________.
7、如图,已知,.若,,则的度数是__________.
8、如图,已知,,则下列结论不成立的是(
).
A.
B.
C.
D.
9、图中,,均是平行线,被直线所截得到的角,其中相等的两个角有(
)对.
A.
B.
C.
D.
10、如图,已知,,,四条直线,,,,则等于(
).
A.
B.
C.
D.
11、如图,直线,,,则__________.
12、如图,,,交的平分线于点,
,则__________.
13、将一副三角尺拼成如图所示的图形,过点作平分,交于点.
()试说明:.
()求的度数.
知识点二:平行线性质的应用
一、平行线与三角形
例1:如图,直线,,,则等于(
).
A.
B.
C.
D.
练习:
1、如图,直线,,,则的度数是(
).
A.
B.
C.
D.
2、如图,直线,,,则的度数是(
).
A.
B.
C.
D.
3、如图,直线,若,,则等于(
).
A.
B.
C.
D.
二、平行线与角平分线
例1:如图,,平分,,则等于(
).
A.
B.
C.
D.
练习:
1、如图,已知,平分,,则为(
).
A.
B.
C.
D.
2、如图,直线,平分,与相交于点,,则
的度数是(
).
A.
B.
C.
D.
3、将一张长方形纸片折叠成如图所示的形状,则(
).
A.
B.
C.
D.
.
三、平行线与垂线
例1:如图①,于点,,,则等于(
).
A.
B.
C.
D.
例2:如图②,直线,于点,,则的度数为(
).
A.
B.
C.
D.
练习:
1、如图,直线,点在直线上,且,,那么的度数是(
).
A.
B.
C.
D.
2、如图,,,垂足为,若,则的度数为(
).
A.
B.
C.
D.
四、平行线与辅助线
例1:如图①,已知,,,则的度数为(
).
A.
B.
C.
D.
例2:如图②,,于点,若,则(
).
A.
B.
C.
D.
例3:如图,直线,若,,则(
).
A.
B.
C.
D.
练习:
如图,的一边为平面镜,,在上有一点,从点射出一束光线经上一点反射,反射光线恰好与平行,则的度数是(
).
A.
B.
C.
D.
2、如图①是我们常用的折叠式小刀,图②中刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图②所示的与,则与的度数和是__________度.
五、平行线与三角尺
例1:小红把一把直尺与一块三角尺如图放置,测得.则的度数为(
).
A.
B.
C.
D.
练习:
1、如图,在平行线,之间放置一块直角三角尺,三角尺的顶点,分别在直线,上,则的值为(
).
A.
B.
C.
D.
2、将一副直角三角尺如图放置,使含角的三角尺的直角边和含角的三角尺的一条直角边在同一条直线上,则的度数为(
).
A.
B.
C.
D.
3、如图,将一副三角尺叠放在一起,使直角的顶点重合于点,,与交于点,则的度数为(
).
A.
B.
C.
D.
4.如图,将一块含有角的直角三角尺的两个顶点放在两条平行的直线,上,如果,那么的度数为(
).
A.
B.
C.
D.
5、如图,将一副三角尺和一张对边平行的纸条按下列方式摆放,两个三角尺的一直角边重合,含角的直角三角尺的斜边与纸条一边重合,含角的三角尺的一个顶点在纸条的另一边上,则的度数是__________.
课堂练习:
1、某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是(
)
A.30°
B.45°
C.60°
D.75°
2、一只因损坏而倾斜的椅子,从背后看到的形状如图所示,其中两组对边的平行关系没有发生变化,若∠1=76°,则∠2的大小是(
)
A.76°
B.86°
C.104°
D.114°
3、如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为(D)
A.60°
B.65°
C.70°
D.75°
4、如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是(
)
A.∠EMB=∠END
B.∠BMN=∠MNC
C.∠CNH=∠BPG
D.∠DNG=∠AME
5、如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(
)
A.60°
B.120°
C.150°
D.180°
6、一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=
°.
7、如图,一只船从点A出发沿北偏东60°方向航行到点B,再以南偏西25°方向返回,则∠ABC=
°.
8、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
9、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
10、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东
°.
11、某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
