北师大版八年级数学上册第一章勾股定理复习学案(无答案)
文档属性
| 名称 | 北师大版八年级数学上册第一章勾股定理复习学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 22:20:03 | ||
图片预览


文档简介
勾股定
考点分析
考点一:勾股定理
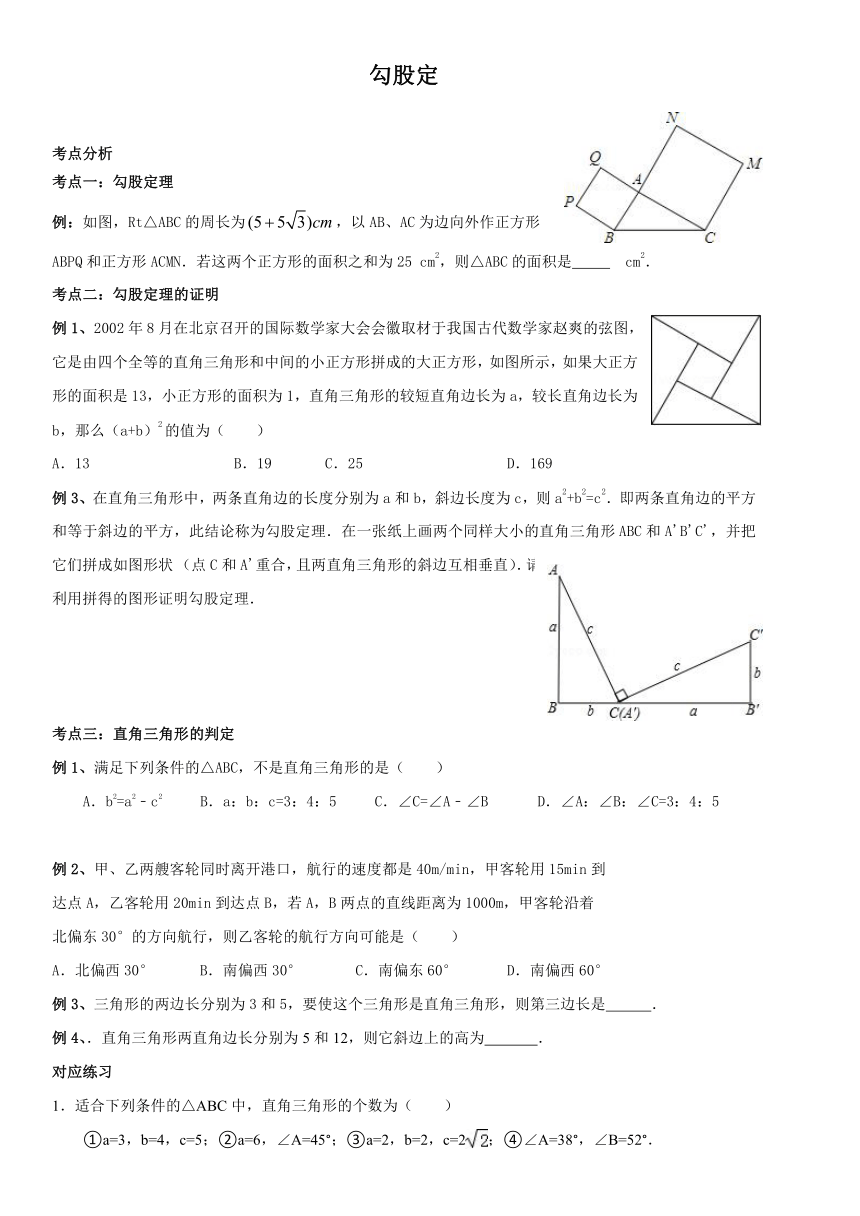
例:如图,Rt△ABC的周长为,以AB、AC为边向外作正方形ABPQ和正方形ACMN.若这两个正方形的面积之和为25
cm2,则△ABC的面积是
cm2.
考点二:勾股定理的证明
例1、2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为(
)
A.13
B.19
C.25
D.169
例3、在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2.即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A'B'C',并把它们拼成如图形状
(点C和A'重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.
考点三:直角三角形的判定
例1、满足下列条件的△ABC,不是直角三角形的是(
)
A.b2=a2﹣c2
B.a:b:c=3:4:5
C.∠C=∠A﹣∠B
D.∠A:∠B:∠C=3:4:5
例2、甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到
达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着
北偏东30°的方向航行,则乙客轮的航行方向可能是(
)
A.北偏西30°
B.南偏西30°
C.南偏东60°
D.南偏西60°
例3、三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三边长是
.
例4、.直角三角形两直角边长分别为5和12,则它斜边上的高为
.
对应练习
1.适合下列条件的△ABC中,直角三角形的个数为(
)
①a=3,b=4,c=5;②a=6,∠A=45°;③a=2,b=2,c=2;④∠A=38°,∠B=52°.
A.1个
B.2个
C.3个
D.4个
2.下列条件中,不能判断△ABC是直角三角形的是( )
A.a:b:c=3:4:5
B.∠A:∠B:∠C=3:4:5
C.∠A+∠B=∠C
D.a:b:c=1:2:
3.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长( )
A.3
B.2
C.4
D.
4.如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )
A.4
B.8
C.16
D.34
4.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.3
B.4
C.15
D.7.2
5.下列各组线段中,不能构成直角三角形的是( )
A.1、、
B.、、
C.2、、
D.1、2、
对应练习
考点一:解直角三角形
例1、如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是
。
例2、如图所示,一个梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了
米.
例3、在一个广场上有两棵树,一棵高8米,另一棵高2米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 米.
例4、一个零件的形状如图所示,已知AC⊥AB,BC⊥BD,AC=3cm,AB=4cm,BD=12cm,求CD的长.
例5、台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20千米/小时,台风影响该海港持续的时间有多长?
考点二:立体图形的最短路径问题
例1、如图,一圆柱高8cm,底面半径为
cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
A.6cm
B.8cm
C.10cm
D.12cm
例2、葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,它的底面周长是50cm,当一段葛藤绕树干盘旋2圈升高为2.4m时,这段葛藤的长是( )m.
A.3
B.2.6
C.2.8
D.2.5
例3、如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为
.
例4、.如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
对应练习
1.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面.然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m.则旗杆高度为( )(滑轮上方的部分忽略不计)
A.12m
B.13m
C.16m
D.17m
2.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A.13cm
B.cm
C.2cm
D.20cm
3.如图,正四棱柱的底面边长为8cm,侧棱长为12cm,一只蚂蚁欲从点A出发,沿棱柱表面到点B处吃食物,那么它所爬行的最短路径是
cm.
4.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要
元钱.
5.如图,轮船甲从港口O出发沿北偏西25°的方向航行8海里,同时轮船乙从港口O出发沿南偏西65°的方向航行15海里,这时两轮船相距
海里.
6.如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
7.如图,圆柱底面圆的半径为cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
8.如图,一个直立放着的无盖长方体铁罐的长、宽、高的长度分别为3,2,10.在罐内部棱CC′中点P处有一滴蜂蜜,此时一只蚂蚁在罐外部的顶点A′处,求蚂蚁到达蜂蜜的最短距离.
考点分析
考点一:勾股定理
例:如图,Rt△ABC的周长为,以AB、AC为边向外作正方形ABPQ和正方形ACMN.若这两个正方形的面积之和为25
cm2,则△ABC的面积是
cm2.
考点二:勾股定理的证明
例1、2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为(
)
A.13
B.19
C.25
D.169
例3、在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2.即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A'B'C',并把它们拼成如图形状
(点C和A'重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.
考点三:直角三角形的判定
例1、满足下列条件的△ABC,不是直角三角形的是(
)
A.b2=a2﹣c2
B.a:b:c=3:4:5
C.∠C=∠A﹣∠B
D.∠A:∠B:∠C=3:4:5
例2、甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到
达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着
北偏东30°的方向航行,则乙客轮的航行方向可能是(
)
A.北偏西30°
B.南偏西30°
C.南偏东60°
D.南偏西60°
例3、三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三边长是
.
例4、.直角三角形两直角边长分别为5和12,则它斜边上的高为
.
对应练习
1.适合下列条件的△ABC中,直角三角形的个数为(
)
①a=3,b=4,c=5;②a=6,∠A=45°;③a=2,b=2,c=2;④∠A=38°,∠B=52°.
A.1个
B.2个
C.3个
D.4个
2.下列条件中,不能判断△ABC是直角三角形的是( )
A.a:b:c=3:4:5
B.∠A:∠B:∠C=3:4:5
C.∠A+∠B=∠C
D.a:b:c=1:2:
3.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长( )
A.3
B.2
C.4
D.
4.如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )
A.4
B.8
C.16
D.34
4.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.3
B.4
C.15
D.7.2
5.下列各组线段中,不能构成直角三角形的是( )
A.1、、
B.、、
C.2、、
D.1、2、
对应练习
考点一:解直角三角形
例1、如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是
。
例2、如图所示,一个梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了
米.
例3、在一个广场上有两棵树,一棵高8米,另一棵高2米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 米.
例4、一个零件的形状如图所示,已知AC⊥AB,BC⊥BD,AC=3cm,AB=4cm,BD=12cm,求CD的长.
例5、台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20千米/小时,台风影响该海港持续的时间有多长?
考点二:立体图形的最短路径问题
例1、如图,一圆柱高8cm,底面半径为
cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
A.6cm
B.8cm
C.10cm
D.12cm
例2、葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,它的底面周长是50cm,当一段葛藤绕树干盘旋2圈升高为2.4m时,这段葛藤的长是( )m.
A.3
B.2.6
C.2.8
D.2.5
例3、如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为
.
例4、.如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
对应练习
1.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面.然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m.则旗杆高度为( )(滑轮上方的部分忽略不计)
A.12m
B.13m
C.16m
D.17m
2.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A.13cm
B.cm
C.2cm
D.20cm
3.如图,正四棱柱的底面边长为8cm,侧棱长为12cm,一只蚂蚁欲从点A出发,沿棱柱表面到点B处吃食物,那么它所爬行的最短路径是
cm.
4.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要
元钱.
5.如图,轮船甲从港口O出发沿北偏西25°的方向航行8海里,同时轮船乙从港口O出发沿南偏西65°的方向航行15海里,这时两轮船相距
海里.
6.如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
7.如图,圆柱底面圆的半径为cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
8.如图,一个直立放着的无盖长方体铁罐的长、宽、高的长度分别为3,2,10.在罐内部棱CC′中点P处有一滴蜂蜜,此时一只蚂蚁在罐外部的顶点A′处,求蚂蚁到达蜂蜜的最短距离.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
