华东师大版数学九年级下册-27.1.2 圆的轴对称性 教案
文档属性
| 名称 | 华东师大版数学九年级下册-27.1.2 圆的轴对称性 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 162.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 15:08:39 | ||
图片预览


文档简介
圆的轴对称性
教学目标:
1、记忆垂经定理。
2、运用垂经定理,构造直角三角形,运用勾股定理,学会弦心距d
半径r
弦a
弓形高h之间的互求。
教学重点:运用垂经定理。
教学设计:
1、通过情景导入提出问题——探讨赵州桥构造,来激发学生兴趣。
2、让学生动手实验观察:直径垂直弦圆地对折,从而猜想、归纳、引出命题、证明命题、形成定理。充分体验探索过程。
3、“1题”是定理证明。让学生能将定理文字表达转化成数学表达、能分清题设和结论、能画出图形、能证明。
4、“练习2”让学生熟悉垂经定理:分清题设、结论、5个要素。
“练习3—6”让学生学会运用垂经定理计算、学会“弦心距d
半径r
弦a
弓形高h”之间的互求,“知二求二”。
5、学生完成本节小结,教师补充小结。
6、“练习7”
让学生运用所学的垂经定理知识解决情景导入提出问题。让学生的兴趣疑问得以解决。
7、“练习8、学生作业”让学生学会运用垂经定理证明。
过程和方法:
教师引导,学生自主学习与小组合作探究相结合的方法。
情感、态度、价值观:
了解赵州桥的知识,知道我国古代劳动人民的聪明才干以及数学知识博大精深。
教学过程:
〔情境导入〕1300多年前,我国隋代建造的赵州桥,桥拱是圆弧形。风风雨雨、饱经沧桑一千多年,赵州桥毅然保持它的雄姿。为什么赵州桥能能存在这么长时间呢?原因之一就是它的构造是石拱形。
这一节我们首先学习圆的知识,然后运用所学知识探讨一下赵州桥构造。
一
复习提问:
〔师〕1、什么是轴对称图形?我们在前面学过哪些轴对称图形?
〔生〕常见轴对称图形有等腰梯形、等腰三角形、矩形、菱形等。如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形。〔师〕2、我们所学的圆是不是轴对称图形呢?对称轴是什么?圆有几条对称轴?
〔生〕圆是轴对称图形。过圆心的直线都是它的对称轴。
有无数条轴对称轴。
二
观察对折
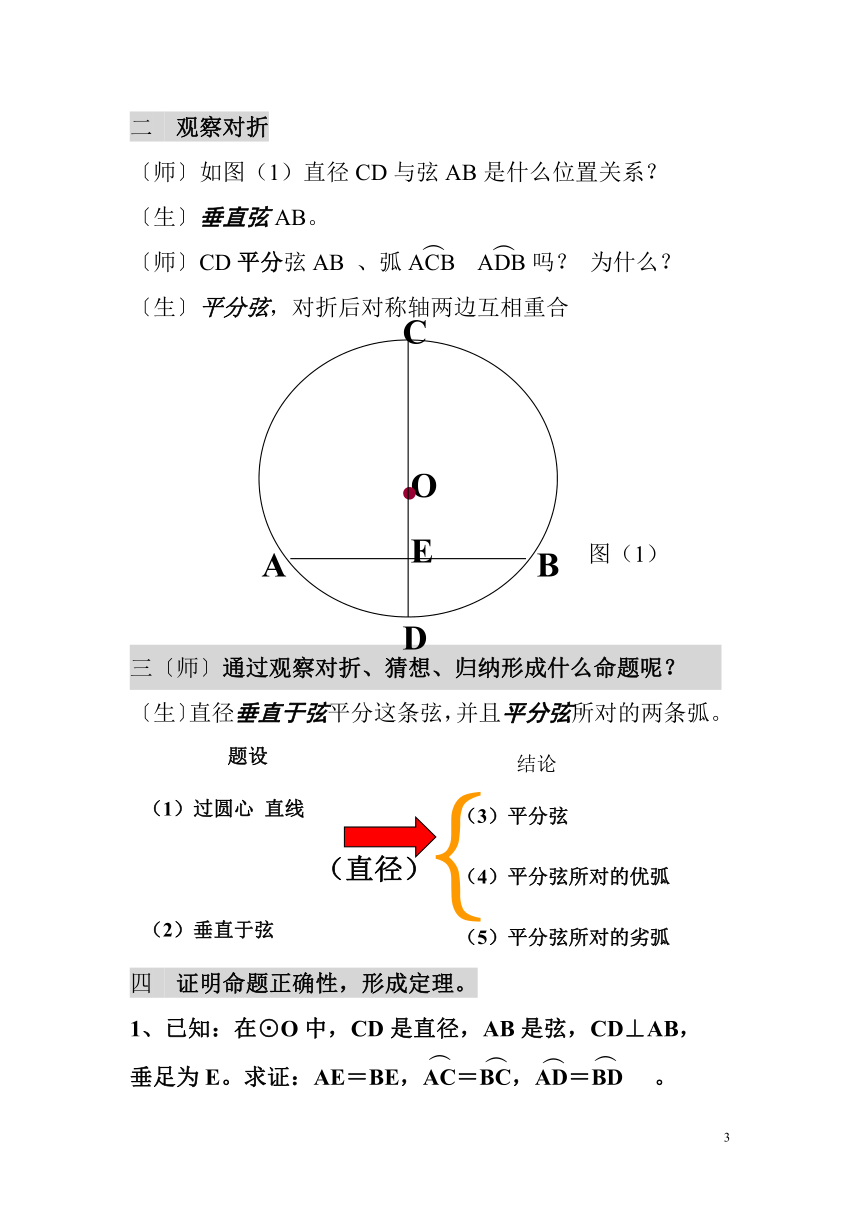
〔师〕如图(1)直径CD与弦AB是什么位置关系?
〔生〕垂直弦AB。
〔师〕CD平分弦AB
、弧ACB
ADB吗?
为什么?
〔生〕平分弦,对折后对称轴两边互相重合
三〔师〕通过观察对折、猜想、归纳形成什么命题呢?
〔生〕直径垂直于弦平分这条弦,并且平分弦所对的两条弧。
四
证明命题正确性,形成定理。
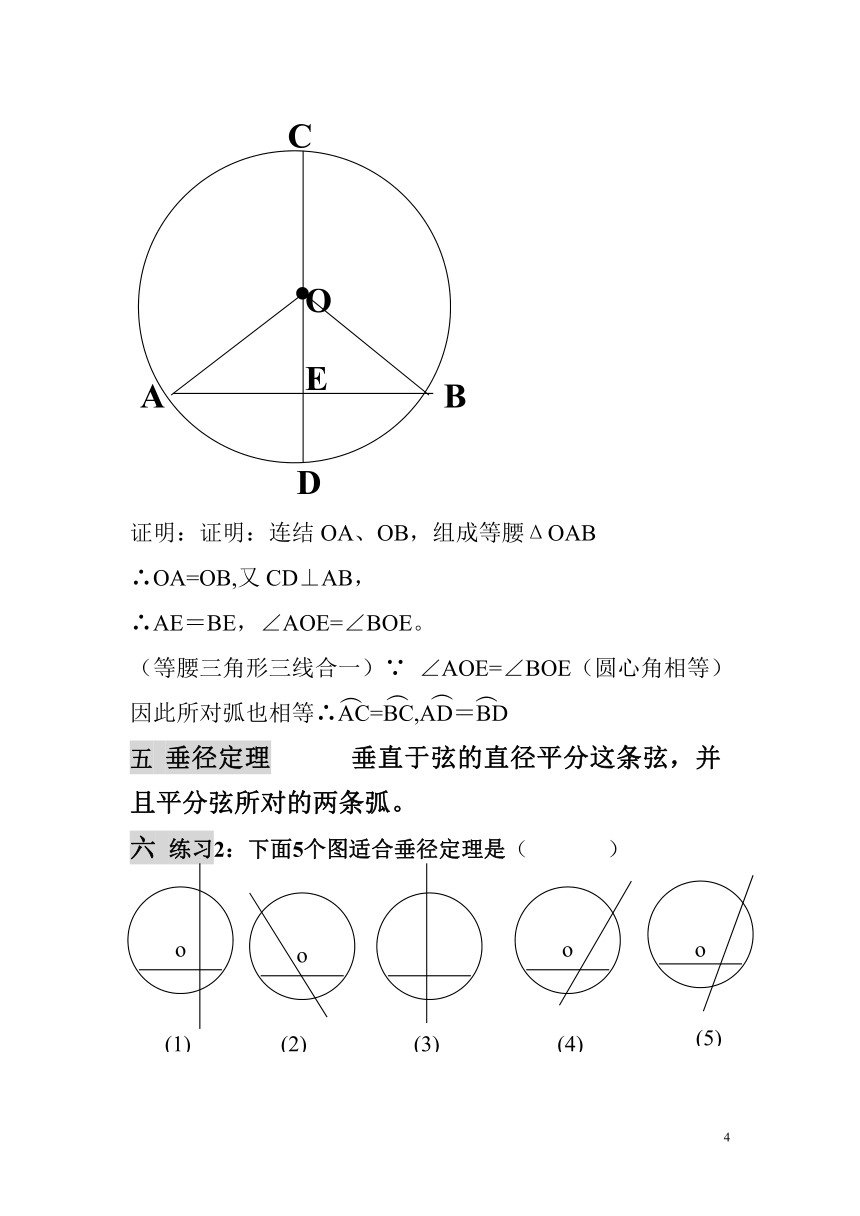
1、已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,
垂足为E。求证:AE=BE,AC=BC,AD=BD。
证明:证明:连结OA、OB,组成等腰ΔOAB
∴OA=OB,又CD⊥AB,
∴AE=BE,∠AOE=∠BOE。
(等腰三角形三线合一)∵
∠AOE=∠BOE(圆心角相等)
因此所对弧也相等∴AC=BC,AD=BD
五
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
六
练习2:下面5个图适合垂径定理是(
)
练习3
如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。
解:连结OA。过O作OE⊥AB,垂足为E,则OE=3厘米,AE=BE。∵AB=8厘米
∴AE=4厘米
在RtAOE中,根据勾股定理有OA=5厘米
∴⊙O的半径为5厘米。
练习4.
如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
OP=3米,OA=5米
,你能求出这个圆的弦AB吗?
练习5.如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
OA=5米AB=8米
,你能求出这个圆的弓形高CP吗?
练习6
如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
CP=2米,AB=8米
,你能求出这个圆的弦心距吗?
七
通过以上题目你有什么启发?
即:1半径
2弦
3弦心距
4弓形高,它们之间如何互求?
小结:1、作辅助线:圆心向弦作垂线。
2、构造直角三角形,利用勾股定理。
3、弦心距d
半径r
弦a
弓形高h。
R2=d2
+
()
2
R2=(r-h)
2
+
()
2
简单的说:
(1)构造直角三角形,运用勾股定理.(2)知二求二.
解决问题练习7
1300多年以前,我国隋代建造的赵州桥,桥拱是圆弧形。它的跨度为37.4米,拱高为7.2米。求桥拱半径。
(
F
37.4m
A
B
E
r
∟
O
)
练习8已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。求证:AC=BD。
证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。所以,AC=BD
八
学生作业
已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF
教学目标:
1、记忆垂经定理。
2、运用垂经定理,构造直角三角形,运用勾股定理,学会弦心距d
半径r
弦a
弓形高h之间的互求。
教学重点:运用垂经定理。
教学设计:
1、通过情景导入提出问题——探讨赵州桥构造,来激发学生兴趣。
2、让学生动手实验观察:直径垂直弦圆地对折,从而猜想、归纳、引出命题、证明命题、形成定理。充分体验探索过程。
3、“1题”是定理证明。让学生能将定理文字表达转化成数学表达、能分清题设和结论、能画出图形、能证明。
4、“练习2”让学生熟悉垂经定理:分清题设、结论、5个要素。
“练习3—6”让学生学会运用垂经定理计算、学会“弦心距d
半径r
弦a
弓形高h”之间的互求,“知二求二”。
5、学生完成本节小结,教师补充小结。
6、“练习7”
让学生运用所学的垂经定理知识解决情景导入提出问题。让学生的兴趣疑问得以解决。
7、“练习8、学生作业”让学生学会运用垂经定理证明。
过程和方法:
教师引导,学生自主学习与小组合作探究相结合的方法。
情感、态度、价值观:
了解赵州桥的知识,知道我国古代劳动人民的聪明才干以及数学知识博大精深。
教学过程:
〔情境导入〕1300多年前,我国隋代建造的赵州桥,桥拱是圆弧形。风风雨雨、饱经沧桑一千多年,赵州桥毅然保持它的雄姿。为什么赵州桥能能存在这么长时间呢?原因之一就是它的构造是石拱形。
这一节我们首先学习圆的知识,然后运用所学知识探讨一下赵州桥构造。
一
复习提问:
〔师〕1、什么是轴对称图形?我们在前面学过哪些轴对称图形?
〔生〕常见轴对称图形有等腰梯形、等腰三角形、矩形、菱形等。如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形。〔师〕2、我们所学的圆是不是轴对称图形呢?对称轴是什么?圆有几条对称轴?
〔生〕圆是轴对称图形。过圆心的直线都是它的对称轴。
有无数条轴对称轴。
二
观察对折
〔师〕如图(1)直径CD与弦AB是什么位置关系?
〔生〕垂直弦AB。
〔师〕CD平分弦AB
、弧ACB
ADB吗?
为什么?
〔生〕平分弦,对折后对称轴两边互相重合
三〔师〕通过观察对折、猜想、归纳形成什么命题呢?
〔生〕直径垂直于弦平分这条弦,并且平分弦所对的两条弧。
四
证明命题正确性,形成定理。
1、已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,
垂足为E。求证:AE=BE,AC=BC,AD=BD。
证明:证明:连结OA、OB,组成等腰ΔOAB
∴OA=OB,又CD⊥AB,
∴AE=BE,∠AOE=∠BOE。
(等腰三角形三线合一)∵
∠AOE=∠BOE(圆心角相等)
因此所对弧也相等∴AC=BC,AD=BD
五
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
六
练习2:下面5个图适合垂径定理是(
)
练习3
如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。
解:连结OA。过O作OE⊥AB,垂足为E,则OE=3厘米,AE=BE。∵AB=8厘米
∴AE=4厘米
在RtAOE中,根据勾股定理有OA=5厘米
∴⊙O的半径为5厘米。
练习4.
如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
OP=3米,OA=5米
,你能求出这个圆的弦AB吗?
练习5.如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
OA=5米AB=8米
,你能求出这个圆的弓形高CP吗?
练习6
如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
CP=2米,AB=8米
,你能求出这个圆的弦心距吗?
七
通过以上题目你有什么启发?
即:1半径
2弦
3弦心距
4弓形高,它们之间如何互求?
小结:1、作辅助线:圆心向弦作垂线。
2、构造直角三角形,利用勾股定理。
3、弦心距d
半径r
弦a
弓形高h。
R2=d2
+
()
2
R2=(r-h)
2
+
()
2
简单的说:
(1)构造直角三角形,运用勾股定理.(2)知二求二.
解决问题练习7
1300多年以前,我国隋代建造的赵州桥,桥拱是圆弧形。它的跨度为37.4米,拱高为7.2米。求桥拱半径。
(
F
37.4m
A
B
E
r
∟
O
)
练习8已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。求证:AC=BD。
证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。所以,AC=BD
八
学生作业
已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF
