人教版八年级数学上册14.2.1 平方差公式教案
文档属性
| 名称 | 人教版八年级数学上册14.2.1 平方差公式教案 |  | |
| 格式 | zip | ||
| 文件大小 | 86.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 20:36:15 | ||
图片预览

文档简介
《14.2.1平方差公式》教学设计
教学目标
知识技能:理解平方差公式,能运用平方差公式进行计算。
过程与方法:经历对平方差公式的探究,培养学生的数形结合和抽象思维能力;
在探索平方差公式的过程中提高学生灵活运用公式解决问题的能力。
情感态度与价值观:让学生感受到数学源于生活,又可应用于生活,提高学习兴趣和信心。
教学重难点
重点:理解和掌握平方差公式;
难点:灵活应用平方差公式(变式)。
教学方法
教法:引导发现法为主,多媒体演示法为辅。
教学手段:多媒体课件
课型;课时:新授课;1课时
教学过程
(一)复习引入
同学们,多项式与多项式是如何相乘的?
(a+b)(m+n)=?
学生利用多项式乘以多项式的法则计算,得出结果。
(a+b)(m+n)==am+an+bm+bn
(二)自主学习
计算下列多项式的积
①(x
+
1)(
x-1);
x2
-
1
②(m
+
2)(
m-2);
m2
-4
③(2m+
1)(2m-1);
4m2
-
1
④(5y
+
z)(5y-z).
25y2
-
z2
(三)合作探究
①(x
+
1)(
x-1);
x2
-
1
②(m
+
2)(
m-2);
m2
-4
③(2m+
1)(2m-1);
4m2
-
1
④(5y
+
z)(5y-z).
25y2
-
z2
想一想:1.每一个式子里面有几个数?
2.每个式子里面等号左右两边有哪些运算?
3.你能用一个公式表示你所发现的规律吗?
(四)成果展示
平方差公式
1.符号表示:(a+b)(a?b)=a2-b2
2.内容:两数和与这两数差的积,等于这两数的平方差.
(五)点拨提升
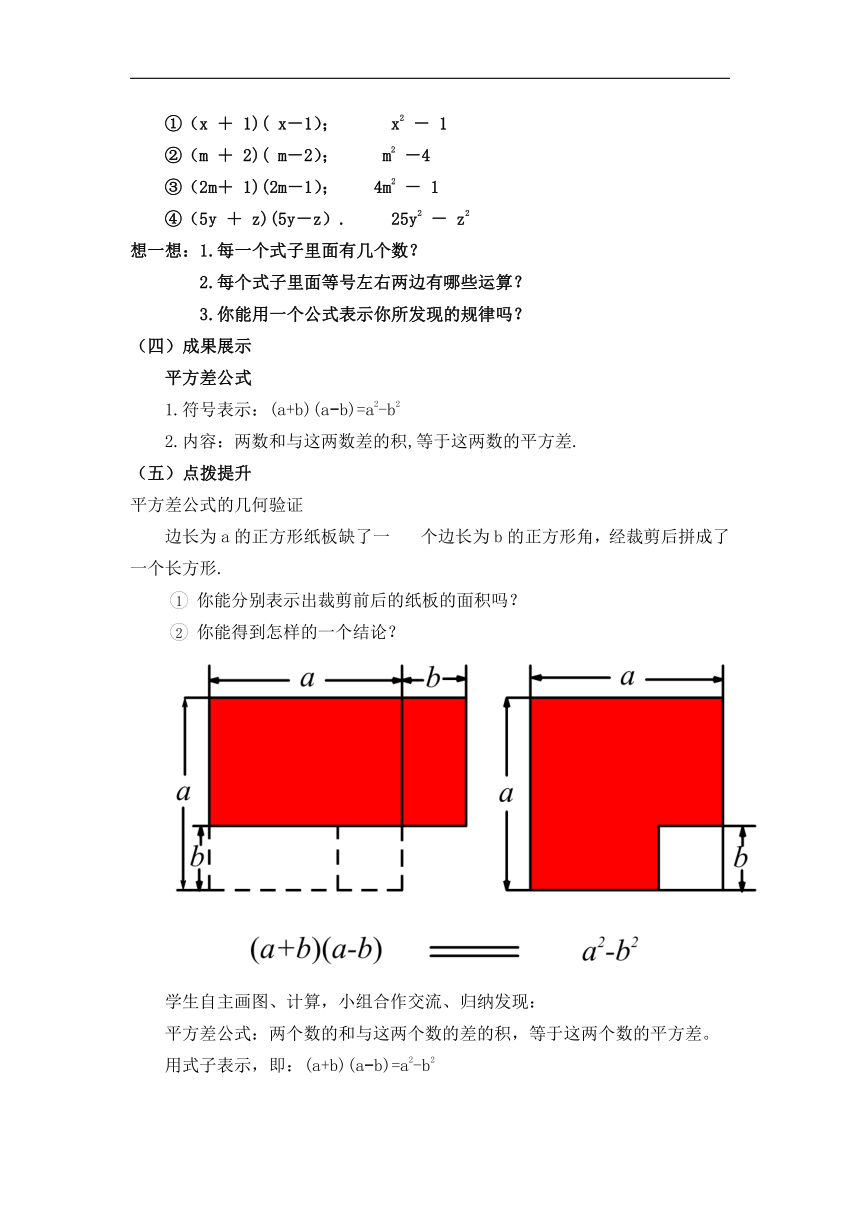
平方差公式的几何验证
边长为a的正方形纸板缺了一个边长为b的正方形角,经裁剪后拼成了一个长方形.
你能分别表示出裁剪前后的纸板的面积吗?
你能得到怎样的一个结论?
学生自主画图、计算,小组合作交流、归纳发现:
平方差公式:两个数的和与这两个数的差的积,等于这两个数的平方差。
用式子表示,即:(a+b)(a?b)=a2-b2
公式变形:
(六)典例精析
例1
计算:(1)
(3x+2
)(
3x-2
)
(2)(-x+2y)(-x-2y)
解:(1)原式=(3x)2-22
=9x2-4
(2)
原式=
(-x)2
-
(2y)2
=x2
-
4y2
(七)巩固练习
利用平方差公式计算:
(1)(3x-5)(3x+5)
(2)(-2a-b)(b-2a)
(3)(-7m+8n)(-8n-7m)
解:(1)原式=(3x)2-52=9x2-25
(2)原式=(-2a)2-b2=4a2-b2
(3)原式=(-7m)2-(8n)2=49m2-64n2
(八)课堂小结
1、试用语言表述平方差公式
两个数的和与这两个数的差的积,等于它们的平方差。
2、应用平方差公式时要注意一些什么?
运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式;
②对于不符合平方差公式标准形式者,要利用加法交换律,或提取两“?”号中的“?”号,变成公式标准形式后,再用公式。
板书设计
14.2.1平方差公式
平方差公式:两数和与这两数差的积,等于这两数的平方差。
用式子表示,即:
公式变形:
计算步骤:1、判断;2、调整;3、分步解。
平方差公式验证
例题
练习
作业布置
作业本:课本112页
习题14.2
第1题
教学反思:
教学目标
知识技能:理解平方差公式,能运用平方差公式进行计算。
过程与方法:经历对平方差公式的探究,培养学生的数形结合和抽象思维能力;
在探索平方差公式的过程中提高学生灵活运用公式解决问题的能力。
情感态度与价值观:让学生感受到数学源于生活,又可应用于生活,提高学习兴趣和信心。
教学重难点
重点:理解和掌握平方差公式;
难点:灵活应用平方差公式(变式)。
教学方法
教法:引导发现法为主,多媒体演示法为辅。
教学手段:多媒体课件
课型;课时:新授课;1课时
教学过程
(一)复习引入
同学们,多项式与多项式是如何相乘的?
(a+b)(m+n)=?
学生利用多项式乘以多项式的法则计算,得出结果。
(a+b)(m+n)==am+an+bm+bn
(二)自主学习
计算下列多项式的积
①(x
+
1)(
x-1);
x2
-
1
②(m
+
2)(
m-2);
m2
-4
③(2m+
1)(2m-1);
4m2
-
1
④(5y
+
z)(5y-z).
25y2
-
z2
(三)合作探究
①(x
+
1)(
x-1);
x2
-
1
②(m
+
2)(
m-2);
m2
-4
③(2m+
1)(2m-1);
4m2
-
1
④(5y
+
z)(5y-z).
25y2
-
z2
想一想:1.每一个式子里面有几个数?
2.每个式子里面等号左右两边有哪些运算?
3.你能用一个公式表示你所发现的规律吗?
(四)成果展示
平方差公式
1.符号表示:(a+b)(a?b)=a2-b2
2.内容:两数和与这两数差的积,等于这两数的平方差.
(五)点拨提升
平方差公式的几何验证
边长为a的正方形纸板缺了一个边长为b的正方形角,经裁剪后拼成了一个长方形.
你能分别表示出裁剪前后的纸板的面积吗?
你能得到怎样的一个结论?
学生自主画图、计算,小组合作交流、归纳发现:
平方差公式:两个数的和与这两个数的差的积,等于这两个数的平方差。
用式子表示,即:(a+b)(a?b)=a2-b2
公式变形:
(六)典例精析
例1
计算:(1)
(3x+2
)(
3x-2
)
(2)(-x+2y)(-x-2y)
解:(1)原式=(3x)2-22
=9x2-4
(2)
原式=
(-x)2
-
(2y)2
=x2
-
4y2
(七)巩固练习
利用平方差公式计算:
(1)(3x-5)(3x+5)
(2)(-2a-b)(b-2a)
(3)(-7m+8n)(-8n-7m)
解:(1)原式=(3x)2-52=9x2-25
(2)原式=(-2a)2-b2=4a2-b2
(3)原式=(-7m)2-(8n)2=49m2-64n2
(八)课堂小结
1、试用语言表述平方差公式
两个数的和与这两个数的差的积,等于它们的平方差。
2、应用平方差公式时要注意一些什么?
运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式;
②对于不符合平方差公式标准形式者,要利用加法交换律,或提取两“?”号中的“?”号,变成公式标准形式后,再用公式。
板书设计
14.2.1平方差公式
平方差公式:两数和与这两数差的积,等于这两数的平方差。
用式子表示,即:
公式变形:
计算步骤:1、判断;2、调整;3、分步解。
平方差公式验证
例题
练习
作业布置
作业本:课本112页
习题14.2
第1题
教学反思:
