人教版八年级数学上册教学案:12.2三角形全等的判定ASA、AAS(5)(表格式)
文档属性
| 名称 | 人教版八年级数学上册教学案:12.2三角形全等的判定ASA、AAS(5)(表格式) |  | |
| 格式 | zip | ||
| 文件大小 | 104.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 20:57:35 | ||
图片预览

文档简介
12.2三角形全等的判定ASA、AAS(5)
年级
八年级
主备人
课型
新授
教学目标
知识与技能:掌握“角边角”及“角角边”条件的内容,能初步应用“角边角”及“角角边”条件判定两个三角形全等.
过程与方法:经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。
情感态度与价值观:通过对问题的共同探讨,培养学生的协作精神。
教学重点
“角边角”条件及“角角边”条件.
教学难点
分析问题,寻找判定两个三角形全等的条件.
教法
启发,讨论,研究
学法
分组讨论,自主归纳
教学过程(师生活动)
复习过程
提出问题
1.复习:(1)三角形中已知三个元素,包括哪几种情况?
三个角、三个边、两边一角、两角一边.
(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?
三种:①定义;②SSS;③SAS.
2.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?
探究新知
深入学习
问题1:三角形中已知两角一边有几种可能?
.两角和它们的夹边.
.两角和其中一角的对边.
(探究)问题2:随意画一个三角形ABC,能不能作一个△A′B′C′,使∠A=∠A′、∠B=∠B′、AB=A′B′呢?
作法:①先用量角器量出∠A与∠B的度数,再用直尺量出AB的边长.
②画线段A′B′,使A′B′=AB.
③分别以A′、B′为顶点,A′B′为一边作∠DA′B′、∠EB′A,使∠D′AB=∠CAB,∠EB′A′=∠CBA.
④射线A′D与B′E交于一点,记为C′
即可得到△A′B′C′.
将△A′B′C′与△ABC重叠,发现两三角形全等.
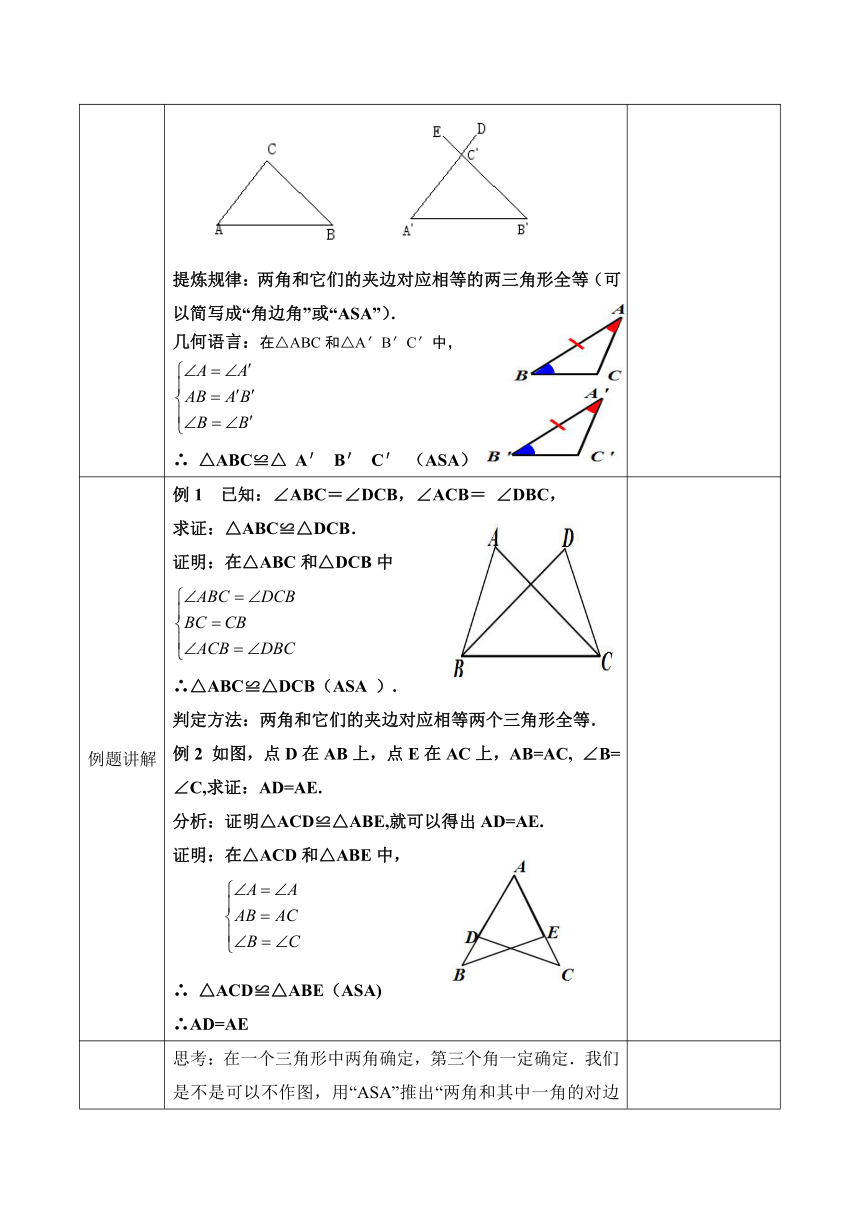
提炼规律:两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA”).
几何语言:在△ABC和△A′B′C′中,
∴
△ABC≌△
A′
B′
C′
(ASA).
例题讲解
例1
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:△ABC≌△DCB.
证明:在△ABC和△DCB中
∴△ABC≌△DCB(ASA
).
判定方法:两角和它们的夹边对应相等两个三角形全等.
例2
如图,点D在AB上,点E在AC上,AB=AC,
∠B=∠C,求证:AD=AE.
分析:证明△ACD≌△ABE,就可以得出AD=AE.
证明:在△ACD和△ABE中,
∴
△ACD≌△ABE(ASA)
∴AD=AE
合作探究
深入学习
思考:在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢?
(探究)问题3:
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180°
∠A=∠D,∠B=∠E
∴∠A+∠B=∠D+∠E
∴∠C=∠F
在△ABC和△DEF中
∴△ABC≌△DEF(ASA).
推论:两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
几何语言表示:在△ABC和△A′B′C′中,
∴
△ABC≌△
A′
B′
C′
(AAS).
例3、已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
课堂练习
练习:图中的两个三角形全等吗?请说明理由.
答案:图(1)中由“ASA”可证得△ACD≌△ACB.图(2)由“AAS”可证得△ACE≌△BDC.
到此为止,在三角形中已知三个条件探索两个三角形全等问题已全部结束.请同学们把两个三角形全等的判定方法作一个小结.
学生活动:自我回忆总结,然后小组讨论交流、补充。
小结与作业
课堂小结
今天我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的两个判定,它们分别是:
角边角公理:两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
推论:两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”。
布置作业
教学反思
年级
八年级
主备人
课型
新授
教学目标
知识与技能:掌握“角边角”及“角角边”条件的内容,能初步应用“角边角”及“角角边”条件判定两个三角形全等.
过程与方法:经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。
情感态度与价值观:通过对问题的共同探讨,培养学生的协作精神。
教学重点
“角边角”条件及“角角边”条件.
教学难点
分析问题,寻找判定两个三角形全等的条件.
教法
启发,讨论,研究
学法
分组讨论,自主归纳
教学过程(师生活动)
复习过程
提出问题
1.复习:(1)三角形中已知三个元素,包括哪几种情况?
三个角、三个边、两边一角、两角一边.
(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?
三种:①定义;②SSS;③SAS.
2.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?
探究新知
深入学习
问题1:三角形中已知两角一边有几种可能?
.两角和它们的夹边.
.两角和其中一角的对边.
(探究)问题2:随意画一个三角形ABC,能不能作一个△A′B′C′,使∠A=∠A′、∠B=∠B′、AB=A′B′呢?
作法:①先用量角器量出∠A与∠B的度数,再用直尺量出AB的边长.
②画线段A′B′,使A′B′=AB.
③分别以A′、B′为顶点,A′B′为一边作∠DA′B′、∠EB′A,使∠D′AB=∠CAB,∠EB′A′=∠CBA.
④射线A′D与B′E交于一点,记为C′
即可得到△A′B′C′.
将△A′B′C′与△ABC重叠,发现两三角形全等.
提炼规律:两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA”).
几何语言:在△ABC和△A′B′C′中,
∴
△ABC≌△
A′
B′
C′
(ASA).
例题讲解
例1
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:△ABC≌△DCB.
证明:在△ABC和△DCB中
∴△ABC≌△DCB(ASA
).
判定方法:两角和它们的夹边对应相等两个三角形全等.
例2
如图,点D在AB上,点E在AC上,AB=AC,
∠B=∠C,求证:AD=AE.
分析:证明△ACD≌△ABE,就可以得出AD=AE.
证明:在△ACD和△ABE中,
∴
△ACD≌△ABE(ASA)
∴AD=AE
合作探究
深入学习
思考:在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢?
(探究)问题3:
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180°
∠A=∠D,∠B=∠E
∴∠A+∠B=∠D+∠E
∴∠C=∠F
在△ABC和△DEF中
∴△ABC≌△DEF(ASA).
推论:两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
几何语言表示:在△ABC和△A′B′C′中,
∴
△ABC≌△
A′
B′
C′
(AAS).
例3、已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
课堂练习
练习:图中的两个三角形全等吗?请说明理由.
答案:图(1)中由“ASA”可证得△ACD≌△ACB.图(2)由“AAS”可证得△ACE≌△BDC.
到此为止,在三角形中已知三个条件探索两个三角形全等问题已全部结束.请同学们把两个三角形全等的判定方法作一个小结.
学生活动:自我回忆总结,然后小组讨论交流、补充。
小结与作业
课堂小结
今天我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的两个判定,它们分别是:
角边角公理:两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
推论:两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”。
布置作业
教学反思
