苏科版 八年级数学上册 3.1 勾股定理 教案(表格式)
文档属性
| 名称 | 苏科版 八年级数学上册 3.1 勾股定理 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 672.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 00:00:00 | ||
图片预览

文档简介
3.1《勾股定理》(1)教学设计
设计者
教学内容
《勾股定理》
学时
一课时
学科(版本)
初中数学·苏科版(八年级上册)
章节
第78-79页
教学目标
1、经历探索勾股定理的过程,发展合情推理的能力,体会数形结合的思想
2、能应用勾股定理求直角三角形中未知边的长
3、发展有条理的思考与表达能力,感受勾股定理的文化价值
学情分析
八年级学生已有直角三角形、正方形等几何图形的基本认识,能利用直尺在方格纸中画出直角三角形和正方形,对图形旋转有一定的认识,有开展合作学习的能力,有初步的“数形结合”思想意识,能进行简单的逻辑推理,有利于探索发现勾股定理。
教学重点
及解决措施
教学重点:探索勾股定理
解决措施:利用flash课件,让学生进行拼一拼、数一数、画一画等操作活动,发现数与形之间的联系,用大量的实践合情推理,探索勾股定理。
教学难点
及解决措施
教学难点:探索发现勾股定理的过程及其中以直角三角形斜边为边长的正方形面积计算和绘制环节
解决措施:课件展示引导学生发现,多种方法演示以直角三角形斜边为边长的正方形面积的计算过程,让学生从大量操作中发现勾股定理。
教学资源
准备
教学一体机(白板)、视频展台
教师:flash教学课件
学生:直尺、方格纸、练习纸等
教学环节
教学内容
活动设计
活动目标
信息技术使用及分析
一、情境引入
观察纪念邮票,初步感知
1、展示1955年希腊为纪念毕达哥拉斯学派根据勾股定理设计并发行的纪念邮票。
2、观察邮票上有哪些图案及图案中各正方形内小方格的个数,你有哪些发现?
激发学生探索勾股定理的热情
【信息技术使用】
展示1955年希腊为纪念毕达哥拉斯学派根据勾股定理设计并发行的纪念邮票。
【使用分析】
运用呈现功能,向学生呈现出放大的、清晰的纪念邮票图片。与课本中图片相比,图像更清晰,便于学生观察。
二、探索活动
探索勾股定理
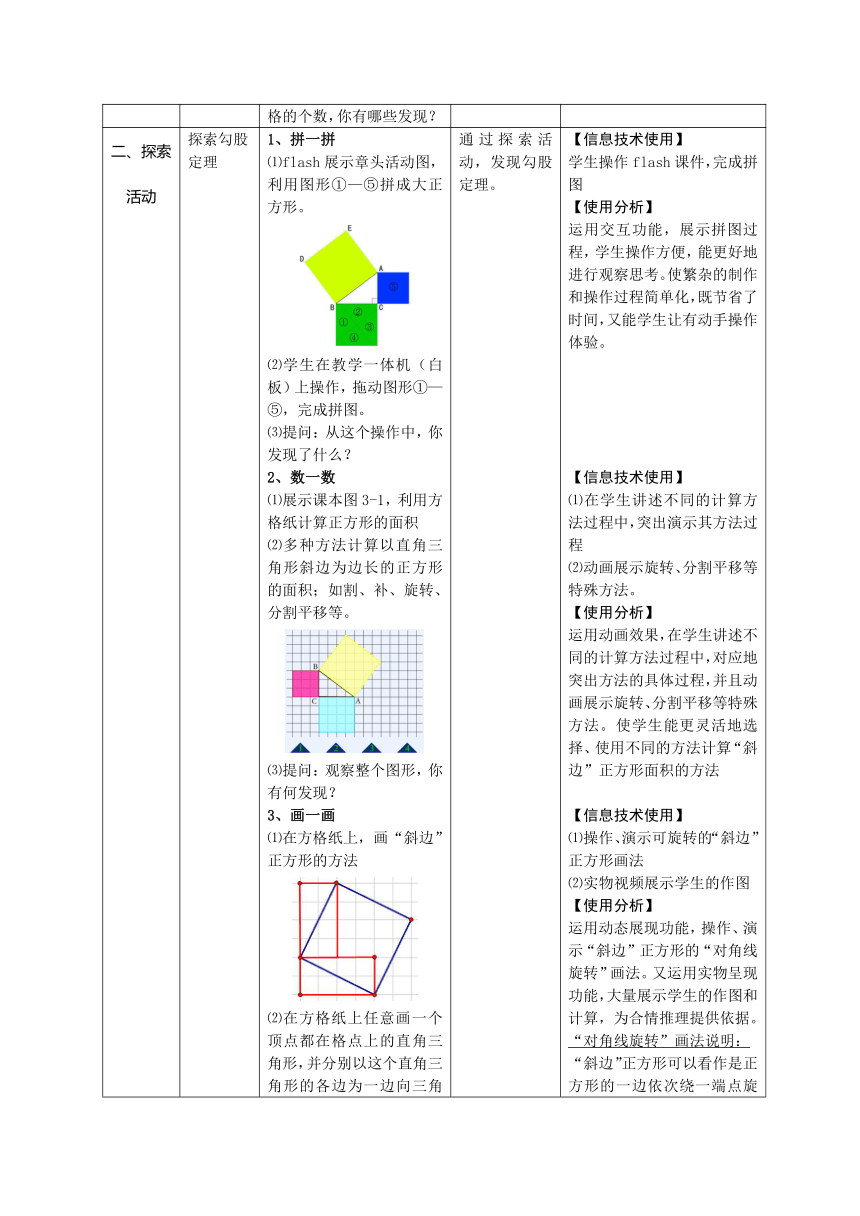
1、拼一拼
⑴flash展示章头活动图,利用图形①—⑤拼成大正方形。
⑵学生在教学一体机(白板)上操作,拖动图形①—⑤,完成拼图。
⑶提问:从这个操作中,你发现了什么?
2、数一数
⑴展示课本图3-1,利用方格纸计算正方形的面积
⑵多种方法计算以直角三角形斜边为边长的正方形的面积;如割、补、旋转、分割平移等。
⑶提问:观察整个图形,你有何发现?
3、画一画
⑴在方格纸上,画“斜边”正方形的方法
⑵在方格纸上任意画一个顶点都在格点上的直角三角形,并分别以这个直角三角形的各边为一边向三角形外部作正方形,并求出各个正方形的面积。
⑶展示学生的操作图
⑷通过大量的实践操作,你能说说直角三角形的三边之间有什么关系?
4、指导归纳
⑴勾股定理
直角三角形两条直角边的平方和等于斜边的平方
⑵勾股定理几何符号表示:在Rt△ABC中,∠C=90°,两条直角边和斜边长分别为,则三边关系为
通过探索活动,发现勾股定理。
【信息技术使用】
学生操作flash课件,完成拼图
【使用分析】
运用交互功能,展示拼图过程,学生操作方便,能更好地进行观察思考。使繁杂的制作和操作过程简单化,既节省了时间,又能学生让有动手操作体验。
【信息技术使用】
⑴在学生讲述不同的计算方法过程中,突出演示其方法过程
⑵动画展示旋转、分割平移等特殊方法。
【使用分析】
运用动画效果,在学生讲述不同的计算方法过程中,对应地突出方法的具体过程,并且动画展示旋转、分割平移等特殊方法。使学生能更灵活地选择、使用不同的方法计算“斜边”正方形面积的方法
【信息技术使用】
⑴操作、演示可旋转的“斜边”正方形画法
⑵实物视频展示学生的作图
【使用分析】
运用动态展现功能,操作、演示“斜边”正方形的“对角线旋转”画法。又运用实物呈现功能,大量展示学生的作图和计算,为合情推理提供依据。
“对角线旋转”画法说明:
“斜边”正方形可以看作是正方形的一边依次绕一端点旋转90°后围成的图形。正方形的一边可以看作某个长方形的对角线,将长方形绕顶点旋转90°对于学生理解起来更容易些。
三、介绍背景
勾股定理的背景介绍
1、观看视频,介绍勾股定理历史。
通过视频观看,让学生感受到勾股定理的文化价值。
【信息技术使用】
播放介绍勾股定理的国内外历史的视频。
【使用分析】
运用精彩的视频更能让学生感受到勾股定理的价值。
四、练习巩固
练习题训练
1、直接运用勾股定理求直角三角形未知边的长
2、运用勾股定理解决简单的实际问题。
巩固勾股定理,运用其解决简单的问题。
【信息技术使用】
对简单应用问题中的实物图进行抽象,演变成直角三角形,再用勾股定理解决。
【使用分析】
运用“淡化”“突显”功能,将实际问题情境中的实物图片抽象成具体的直角三角形,能更好地帮助学生分析问题、解决问题。
五、全课小结
通过这节课学习,你掌握了什么知识?还想知道些什么呢?
回顾学习内容
板书设计:
3.1
勾股定理
1、内容:直角三角形两条直角边的平方和等于斜边的平方
2、几何符号:
教学流程图:
设计者
教学内容
《勾股定理》
学时
一课时
学科(版本)
初中数学·苏科版(八年级上册)
章节
第78-79页
教学目标
1、经历探索勾股定理的过程,发展合情推理的能力,体会数形结合的思想
2、能应用勾股定理求直角三角形中未知边的长
3、发展有条理的思考与表达能力,感受勾股定理的文化价值
学情分析
八年级学生已有直角三角形、正方形等几何图形的基本认识,能利用直尺在方格纸中画出直角三角形和正方形,对图形旋转有一定的认识,有开展合作学习的能力,有初步的“数形结合”思想意识,能进行简单的逻辑推理,有利于探索发现勾股定理。
教学重点
及解决措施
教学重点:探索勾股定理
解决措施:利用flash课件,让学生进行拼一拼、数一数、画一画等操作活动,发现数与形之间的联系,用大量的实践合情推理,探索勾股定理。
教学难点
及解决措施
教学难点:探索发现勾股定理的过程及其中以直角三角形斜边为边长的正方形面积计算和绘制环节
解决措施:课件展示引导学生发现,多种方法演示以直角三角形斜边为边长的正方形面积的计算过程,让学生从大量操作中发现勾股定理。
教学资源
准备
教学一体机(白板)、视频展台
教师:flash教学课件
学生:直尺、方格纸、练习纸等
教学环节
教学内容
活动设计
活动目标
信息技术使用及分析
一、情境引入
观察纪念邮票,初步感知
1、展示1955年希腊为纪念毕达哥拉斯学派根据勾股定理设计并发行的纪念邮票。
2、观察邮票上有哪些图案及图案中各正方形内小方格的个数,你有哪些发现?
激发学生探索勾股定理的热情
【信息技术使用】
展示1955年希腊为纪念毕达哥拉斯学派根据勾股定理设计并发行的纪念邮票。
【使用分析】
运用呈现功能,向学生呈现出放大的、清晰的纪念邮票图片。与课本中图片相比,图像更清晰,便于学生观察。
二、探索活动
探索勾股定理
1、拼一拼
⑴flash展示章头活动图,利用图形①—⑤拼成大正方形。
⑵学生在教学一体机(白板)上操作,拖动图形①—⑤,完成拼图。
⑶提问:从这个操作中,你发现了什么?
2、数一数
⑴展示课本图3-1,利用方格纸计算正方形的面积
⑵多种方法计算以直角三角形斜边为边长的正方形的面积;如割、补、旋转、分割平移等。
⑶提问:观察整个图形,你有何发现?
3、画一画
⑴在方格纸上,画“斜边”正方形的方法
⑵在方格纸上任意画一个顶点都在格点上的直角三角形,并分别以这个直角三角形的各边为一边向三角形外部作正方形,并求出各个正方形的面积。
⑶展示学生的操作图
⑷通过大量的实践操作,你能说说直角三角形的三边之间有什么关系?
4、指导归纳
⑴勾股定理
直角三角形两条直角边的平方和等于斜边的平方
⑵勾股定理几何符号表示:在Rt△ABC中,∠C=90°,两条直角边和斜边长分别为,则三边关系为
通过探索活动,发现勾股定理。
【信息技术使用】
学生操作flash课件,完成拼图
【使用分析】
运用交互功能,展示拼图过程,学生操作方便,能更好地进行观察思考。使繁杂的制作和操作过程简单化,既节省了时间,又能学生让有动手操作体验。
【信息技术使用】
⑴在学生讲述不同的计算方法过程中,突出演示其方法过程
⑵动画展示旋转、分割平移等特殊方法。
【使用分析】
运用动画效果,在学生讲述不同的计算方法过程中,对应地突出方法的具体过程,并且动画展示旋转、分割平移等特殊方法。使学生能更灵活地选择、使用不同的方法计算“斜边”正方形面积的方法
【信息技术使用】
⑴操作、演示可旋转的“斜边”正方形画法
⑵实物视频展示学生的作图
【使用分析】
运用动态展现功能,操作、演示“斜边”正方形的“对角线旋转”画法。又运用实物呈现功能,大量展示学生的作图和计算,为合情推理提供依据。
“对角线旋转”画法说明:
“斜边”正方形可以看作是正方形的一边依次绕一端点旋转90°后围成的图形。正方形的一边可以看作某个长方形的对角线,将长方形绕顶点旋转90°对于学生理解起来更容易些。
三、介绍背景
勾股定理的背景介绍
1、观看视频,介绍勾股定理历史。
通过视频观看,让学生感受到勾股定理的文化价值。
【信息技术使用】
播放介绍勾股定理的国内外历史的视频。
【使用分析】
运用精彩的视频更能让学生感受到勾股定理的价值。
四、练习巩固
练习题训练
1、直接运用勾股定理求直角三角形未知边的长
2、运用勾股定理解决简单的实际问题。
巩固勾股定理,运用其解决简单的问题。
【信息技术使用】
对简单应用问题中的实物图进行抽象,演变成直角三角形,再用勾股定理解决。
【使用分析】
运用“淡化”“突显”功能,将实际问题情境中的实物图片抽象成具体的直角三角形,能更好地帮助学生分析问题、解决问题。
五、全课小结
通过这节课学习,你掌握了什么知识?还想知道些什么呢?
回顾学习内容
板书设计:
3.1
勾股定理
1、内容:直角三角形两条直角边的平方和等于斜边的平方
2、几何符号:
教学流程图:
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
