人教版八年级下册数学 17.2勾股定理的逆定理 同步练习(Word版含解析)
文档属性
| 名称 | 人教版八年级下册数学 17.2勾股定理的逆定理 同步练习(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 119.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 07:42:12 | ||
图片预览



文档简介
17.2勾股定理的逆定理 同步练习
一.选择题
1.下面的每组数分别是一个三角形的三边长,其中能构成直角三角形的是( )
A.,, B.2,2,5 C.32,42,52 D.3,4,5
2.在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,下列条件中不能说明△ABC是直角三角形的是( )
A.b2=a2﹣c2 B.∠C=∠A+∠B
C.∠A:∠B:∠C=3:4:5 D.a:b:c=5:12:13
3.三角形三边长分别为①3,4,5②5,12,13③17,8,15④1,3,2.其中直角三角形有( )
A.1个 B.2个 C.3个 D.4个
4.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3
B.三边长的平方之比为1:2:3
C.三边长之比为3:4:5
D.三内角之比为3:4:5
5.若一个三角形三边满足(a+b)2﹣c2=2ab,则这个三角形是( )
A.直角三角形 B.等腰直角三角形
C.等腰三角形 D.以上结论都不对
6.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A﹣∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2﹣c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
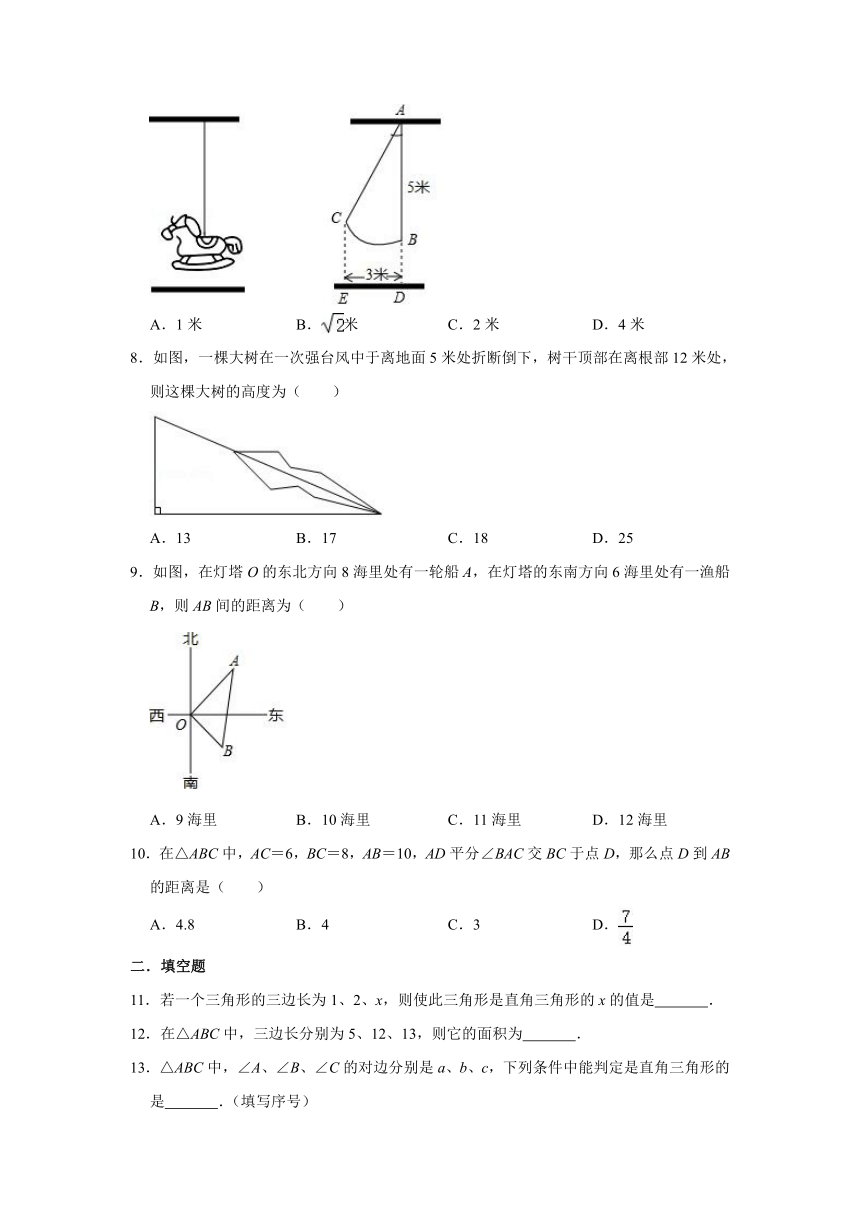
7.如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( )
A.1米 B.米 C.2米 D.4米
8.如图,一棵大树在一次强台风中于离地面5米处折断倒下,树干顶部在离根部12米处,则这棵大树的高度为( )
A.13 B.17 C.18 D.25
9.如图,在灯塔O的东北方向8海里处有一轮船A,在灯塔的东南方向6海里处有一渔船B,则AB间的距离为( )
A.9海里 B.10海里 C.11海里 D.12海里
10.在△ABC中,AC=6,BC=8,AB=10,AD平分∠BAC交BC于点D,那么点D到AB的距离是( )
A.4.8 B.4 C.3 D.
二.填空题
11.若一个三角形的三边长为1、2、x,则使此三角形是直角三角形的x的值是 .
12.在△ABC中,三边长分别为5、12、13,则它的面积为 .
13.△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中能判定是直角三角形的是 .(填写序号)
(1)a:b:c=5:12:13,(2)a=1.5,b=2.5,c=2,(3)(a﹣b)2+2ab=c2,(4)∠A:∠B:∠C=3:4:5,(5)a=n2﹣1,b=2n,c=n2+1(n为大于1的正整数)
14.木工师傅为了让尺子经久耐用,常常在尺子的直角顶点A处与斜边BC之间加一根小木条AD.已知∠BAC=90°,AB=5dm,AC=12dm,则小木条AD的最短长度为 dm.
15.若正整数a,n满足a2+n2=(n+1)2,这样的三个整数a,n,n+1(如:3,4,5或5,12,13)我们称它们为一组“完美勾股数”.当n<150时,共有 组这样的“完美勾股数”.
三.解答题
16.在△ABC中,D是BC上一点,AB=10,BD=6,AD=8,AC=17,求△ABC的面积.
17.如图,已知在△ABC中,CD⊥AB于D,AC=4,BC=3,BD=.
(1)求AD= ;
(2)求证:△ABC是直角三角形.
18.如图是一块四边形木板,其中AB=16cm,BC=24cm,CD=9cm,AD=25cm,∠B=∠C=90°.李师傅找到BC边的中点P,连接AP,DP,发现△APD是直角三角形,请你通过计算说明理由.
参考答案
一.选择题
1.解:A、()2+()2≠()2,故不能构成直角三角形,故此选项不符合题意;
B、22+22≠52,故不能构成直角三角形,故此选项不符合题意
C、因为32=9,42=16,52=25,92+162≠252,故不能构成直角三角形,故此选项不符合题意;
D、32+42=52,故能构成直角三角形,故此选项符合题意.
故选:D.
2.解:A、b2=a2﹣c2,即a2=b2+c2,符合勾股定理的逆定理,能够判定△ABC为直角三角形,不符合题意;
B、∠C=∠A+∠B,此时∠C是直角,能够判定△ABC是直角三角形,不符合题意;
C、∠A:∠B:∠C=3:4:5,那么∠A=45°、∠B=60°、∠C=75°,△ABC不是直角三角形,符合题意;
D、132=52+122,符合勾股定理的逆定理,能够判定△ABC为直角三角形,不符合题意.
故选:C.
3.解:①32+42=52,符合勾股定理的逆定理,能构成直角三角形;
②52+122=132,符合勾股定理的逆定理,能构成直角三角形;
③82+152=172,符合勾股定理的逆定理,能构成直角三角形;
④12+(2)2=32,符合勾股定理的逆定理,能构成直角三角形.
故选:D.
4.解:A、根据三角形内角和公式,求得各角分别为30°,60°,90°,所以此三角形是直角三角形;
B、三边符合勾股定理的逆定理,所以其是直角三角形;
C、32+42=52,符合勾股定理的逆定理,所以是直角三角形;
D、根据三角形内角和公式,求得各角分别为45°,60°,75°,所以此三角形不是直角三角形;
故选:D.
5.解:∵(a+b)2﹣c2=2ab,
∴a2+b2+2ab﹣c2=2ab,
∴a2+b2=c2,
∴这个三角形为直角三角形.
故选:A.
6.解:如果∠A﹣∠B=∠C,那么△ABC是直角三角形,A正确;
如果a2=b2﹣c2,那么△ABC是直角三角形且∠B=90°,B错误;
如果∠A:∠B:∠C=1:3:2,
设∠A=x,则∠B=2x,∠C=3x,
则x+3x+2x=180°,
解得,x=30°,
则3x=90°,
那么△ABC是直角三角形,C正确;
如果a2:b2:c2=9:16:25,
则如果a2+b2=c2,
那么△ABC是直角三角形,D正确;
故选:B.
7.解:过点C作CF⊥AB于点F,
根据题意得:AB=AC=5,CF=DE=3,
由勾股定理可得AF2+CF2=AC2,
∴AF=,
∴BF=AB﹣AF=5﹣4=1,
∴此时木马上升的高度为1米,
故选:A.
8.解:由勾股定理得,BC==13(m).
则大树折断前的高度为:13+5=18(m).
故选:C.
9.解:已知东北方向和东南方向刚好是一直角,
∴∠AOB=90°,
又∵OA=8海里,OB=6海里,
∴AB==10(海里).
故选:B.
10.解:如图,过点D作DE⊥AB于E,
在△ABC中,AC=6,BC=8,AB=10,
∴62+82=102,
∴△ABC是直角三角形,∠C=90°,
∵AD平分∠BAC,
∴CD=ED,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,
∴BE=AB﹣AE=10﹣6=4,
设CD=DE=x,则BD=8﹣x,
在Rt△BDE中,DE2+BE2=BD2,
x2+42=(8﹣x)2,
解得x=3.
故DE的长为3.
故选:C.
二.填空题
11.解:设第三边为x,
(1)若2是直角边,则第三边x是斜边,由勾股定理,得:
12+22=x2,所以x=;
(2)若2是斜边,则第三边x为直角边,由勾股定理,得:
12+x2=22,所以x=;
综上所述:x的值为或,
故答案为:或.
12.解:在△ABC中,三边长分别为5、12、13,
∵52+122=132,
∴三角形是直角三角形,
∴面积为×5×12=30.
故答案为:30.
13.解:(1)(5x)2+(12x)2=(13x)2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
(2)(1.5)2+(2)2=(2.5)2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
(3)由(a﹣b)2+2ab=c2,可得:a2+b2=c2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
(4)∠A:∠B:∠C=3:4:5,此时∠C=100°,不能够判断△ABC是直角三角形,不符合题意;
(5)(n2﹣1)2+(2n)2=(n2+1)2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
故答案为:(1)(2)(3)(5).
14.解:∵∠BAC=90°,AB=5dm,AC=12dm,
∴BC===13(dm),
当AD⊥BC时,AD最短,则AD×BC=AB×AC,
则AD===(dm).
故答案是:.
15.解:∵n<150,(n+1)2﹣n2=2n+1,
又∵149+150=299,大于等于9小于297的非偶数完全平方数有9,25,49,81,121,169,225,289,一共8个,
∴共有8组这样的“完美勾股数”.
故答案为:8.
三.解答题
16.解:∵BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,
∴AD⊥BC,
在Rt△ACD中,CD==15,
∴BC=BD+CD=6+15=21,
∴S△ABC=BC?AD=×21×8=84.
因此△ABC的面积为84.
故答案为84.
17.(1)解:∵CD⊥AB,
∴∠BDC=∠ADC=90°,
在Rt△BDC中,由勾股定理得:CD===,
在Rt△ADC中,由勾股定理得:AD===,
故答案为:;
(2)证明:由(1)知:AD=,
∵BD=,
∴AB=BD+AD=+=5,
∵BC=3,AC=4,
∴AC2+BC2=AB2,
∴∠ACB=90°,
即△ABC是直角三角形.
18.解:∵点P为BC中点,
∴BP=CP=BC=12(cm),
∵∠B=90°,
在Rt△ABP中,根据勾股定理可得:AB2+BP2=AP2,
162+122=AP2,
解得:AP=20(cm),
同理可得:DP=15(cm),
∵152+202=252,
∴AP2+DP2=AD2,
∴△APD是直角三角形,∠APD=90°.
一.选择题
1.下面的每组数分别是一个三角形的三边长,其中能构成直角三角形的是( )
A.,, B.2,2,5 C.32,42,52 D.3,4,5
2.在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,下列条件中不能说明△ABC是直角三角形的是( )
A.b2=a2﹣c2 B.∠C=∠A+∠B
C.∠A:∠B:∠C=3:4:5 D.a:b:c=5:12:13
3.三角形三边长分别为①3,4,5②5,12,13③17,8,15④1,3,2.其中直角三角形有( )
A.1个 B.2个 C.3个 D.4个
4.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3
B.三边长的平方之比为1:2:3
C.三边长之比为3:4:5
D.三内角之比为3:4:5
5.若一个三角形三边满足(a+b)2﹣c2=2ab,则这个三角形是( )
A.直角三角形 B.等腰直角三角形
C.等腰三角形 D.以上结论都不对
6.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A﹣∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2﹣c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
7.如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( )
A.1米 B.米 C.2米 D.4米
8.如图,一棵大树在一次强台风中于离地面5米处折断倒下,树干顶部在离根部12米处,则这棵大树的高度为( )
A.13 B.17 C.18 D.25
9.如图,在灯塔O的东北方向8海里处有一轮船A,在灯塔的东南方向6海里处有一渔船B,则AB间的距离为( )
A.9海里 B.10海里 C.11海里 D.12海里
10.在△ABC中,AC=6,BC=8,AB=10,AD平分∠BAC交BC于点D,那么点D到AB的距离是( )
A.4.8 B.4 C.3 D.
二.填空题
11.若一个三角形的三边长为1、2、x,则使此三角形是直角三角形的x的值是 .
12.在△ABC中,三边长分别为5、12、13,则它的面积为 .
13.△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中能判定是直角三角形的是 .(填写序号)
(1)a:b:c=5:12:13,(2)a=1.5,b=2.5,c=2,(3)(a﹣b)2+2ab=c2,(4)∠A:∠B:∠C=3:4:5,(5)a=n2﹣1,b=2n,c=n2+1(n为大于1的正整数)
14.木工师傅为了让尺子经久耐用,常常在尺子的直角顶点A处与斜边BC之间加一根小木条AD.已知∠BAC=90°,AB=5dm,AC=12dm,则小木条AD的最短长度为 dm.
15.若正整数a,n满足a2+n2=(n+1)2,这样的三个整数a,n,n+1(如:3,4,5或5,12,13)我们称它们为一组“完美勾股数”.当n<150时,共有 组这样的“完美勾股数”.
三.解答题
16.在△ABC中,D是BC上一点,AB=10,BD=6,AD=8,AC=17,求△ABC的面积.
17.如图,已知在△ABC中,CD⊥AB于D,AC=4,BC=3,BD=.
(1)求AD= ;
(2)求证:△ABC是直角三角形.
18.如图是一块四边形木板,其中AB=16cm,BC=24cm,CD=9cm,AD=25cm,∠B=∠C=90°.李师傅找到BC边的中点P,连接AP,DP,发现△APD是直角三角形,请你通过计算说明理由.
参考答案
一.选择题
1.解:A、()2+()2≠()2,故不能构成直角三角形,故此选项不符合题意;
B、22+22≠52,故不能构成直角三角形,故此选项不符合题意
C、因为32=9,42=16,52=25,92+162≠252,故不能构成直角三角形,故此选项不符合题意;
D、32+42=52,故能构成直角三角形,故此选项符合题意.
故选:D.
2.解:A、b2=a2﹣c2,即a2=b2+c2,符合勾股定理的逆定理,能够判定△ABC为直角三角形,不符合题意;
B、∠C=∠A+∠B,此时∠C是直角,能够判定△ABC是直角三角形,不符合题意;
C、∠A:∠B:∠C=3:4:5,那么∠A=45°、∠B=60°、∠C=75°,△ABC不是直角三角形,符合题意;
D、132=52+122,符合勾股定理的逆定理,能够判定△ABC为直角三角形,不符合题意.
故选:C.
3.解:①32+42=52,符合勾股定理的逆定理,能构成直角三角形;
②52+122=132,符合勾股定理的逆定理,能构成直角三角形;
③82+152=172,符合勾股定理的逆定理,能构成直角三角形;
④12+(2)2=32,符合勾股定理的逆定理,能构成直角三角形.
故选:D.
4.解:A、根据三角形内角和公式,求得各角分别为30°,60°,90°,所以此三角形是直角三角形;
B、三边符合勾股定理的逆定理,所以其是直角三角形;
C、32+42=52,符合勾股定理的逆定理,所以是直角三角形;
D、根据三角形内角和公式,求得各角分别为45°,60°,75°,所以此三角形不是直角三角形;
故选:D.
5.解:∵(a+b)2﹣c2=2ab,
∴a2+b2+2ab﹣c2=2ab,
∴a2+b2=c2,
∴这个三角形为直角三角形.
故选:A.
6.解:如果∠A﹣∠B=∠C,那么△ABC是直角三角形,A正确;
如果a2=b2﹣c2,那么△ABC是直角三角形且∠B=90°,B错误;
如果∠A:∠B:∠C=1:3:2,
设∠A=x,则∠B=2x,∠C=3x,
则x+3x+2x=180°,
解得,x=30°,
则3x=90°,
那么△ABC是直角三角形,C正确;
如果a2:b2:c2=9:16:25,
则如果a2+b2=c2,
那么△ABC是直角三角形,D正确;
故选:B.
7.解:过点C作CF⊥AB于点F,
根据题意得:AB=AC=5,CF=DE=3,
由勾股定理可得AF2+CF2=AC2,
∴AF=,
∴BF=AB﹣AF=5﹣4=1,
∴此时木马上升的高度为1米,
故选:A.
8.解:由勾股定理得,BC==13(m).
则大树折断前的高度为:13+5=18(m).
故选:C.
9.解:已知东北方向和东南方向刚好是一直角,
∴∠AOB=90°,
又∵OA=8海里,OB=6海里,
∴AB==10(海里).
故选:B.
10.解:如图,过点D作DE⊥AB于E,
在△ABC中,AC=6,BC=8,AB=10,
∴62+82=102,
∴△ABC是直角三角形,∠C=90°,
∵AD平分∠BAC,
∴CD=ED,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,
∴BE=AB﹣AE=10﹣6=4,
设CD=DE=x,则BD=8﹣x,
在Rt△BDE中,DE2+BE2=BD2,
x2+42=(8﹣x)2,
解得x=3.
故DE的长为3.
故选:C.
二.填空题
11.解:设第三边为x,
(1)若2是直角边,则第三边x是斜边,由勾股定理,得:
12+22=x2,所以x=;
(2)若2是斜边,则第三边x为直角边,由勾股定理,得:
12+x2=22,所以x=;
综上所述:x的值为或,
故答案为:或.
12.解:在△ABC中,三边长分别为5、12、13,
∵52+122=132,
∴三角形是直角三角形,
∴面积为×5×12=30.
故答案为:30.
13.解:(1)(5x)2+(12x)2=(13x)2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
(2)(1.5)2+(2)2=(2.5)2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
(3)由(a﹣b)2+2ab=c2,可得:a2+b2=c2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
(4)∠A:∠B:∠C=3:4:5,此时∠C=100°,不能够判断△ABC是直角三角形,不符合题意;
(5)(n2﹣1)2+(2n)2=(n2+1)2,符合勾股定理的逆定理,能够判断△ABC是直角三角形,符合题意;
故答案为:(1)(2)(3)(5).
14.解:∵∠BAC=90°,AB=5dm,AC=12dm,
∴BC===13(dm),
当AD⊥BC时,AD最短,则AD×BC=AB×AC,
则AD===(dm).
故答案是:.
15.解:∵n<150,(n+1)2﹣n2=2n+1,
又∵149+150=299,大于等于9小于297的非偶数完全平方数有9,25,49,81,121,169,225,289,一共8个,
∴共有8组这样的“完美勾股数”.
故答案为:8.
三.解答题
16.解:∵BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,
∴AD⊥BC,
在Rt△ACD中,CD==15,
∴BC=BD+CD=6+15=21,
∴S△ABC=BC?AD=×21×8=84.
因此△ABC的面积为84.
故答案为84.
17.(1)解:∵CD⊥AB,
∴∠BDC=∠ADC=90°,
在Rt△BDC中,由勾股定理得:CD===,
在Rt△ADC中,由勾股定理得:AD===,
故答案为:;
(2)证明:由(1)知:AD=,
∵BD=,
∴AB=BD+AD=+=5,
∵BC=3,AC=4,
∴AC2+BC2=AB2,
∴∠ACB=90°,
即△ABC是直角三角形.
18.解:∵点P为BC中点,
∴BP=CP=BC=12(cm),
∵∠B=90°,
在Rt△ABP中,根据勾股定理可得:AB2+BP2=AP2,
162+122=AP2,
解得:AP=20(cm),
同理可得:DP=15(cm),
∵152+202=252,
∴AP2+DP2=AD2,
∴△APD是直角三角形,∠APD=90°.
