人教版九年级数学下册 第27章 相似 单元测试题(Word版 有答案)
文档属性
| 名称 | 人教版九年级数学下册 第27章 相似 单元测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 180.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 07:12:28 | ||
图片预览

文档简介
1049020010693400123190000第27章 相似 单元测试题
(满分100分;时间:90分钟)
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
?1. 下列说法不一定正确的是( )
A.所有的等边三角形都相似 B.所有的等腰直角三角形都相似
C.所有的菱形都相似 D.所有的正方形都相似
?2. 如图,四边形ABCD?四边形EFGH,若 ∠A=∠D=100?,∠G=65?,则∠F=(? ? ? ? )
A.65? B.95? C.100? D.105?
?
3. 在△ABC中,DE?//?BC,AD=6,DB=3,AE=4,则EC的长为(? ? ? ??)
A.1 B.2 C.3 D.4
?
4. 若a3=b4=c5,则a+bb+c的值为( )
A.79 B.43 C.45 D.87
?
5. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,ODDA=23,则△DEF与△ABC的面积比为( )
A.2:3 B.4:9 C.2:5 D.4:25
?
6. 三条线段满足ab=bc,若a=2,c=8,则b的长度为( )
A.±4 B.4 C.2 D.6
?
7. 下列说法不正确的是( )
A.含30?角的直角三角形与含60?角的直角三角形是相似的
B.所有的矩形是相似的
C.所有边数相等的正多边形是相似的
D.所有的等边三角形都是相似的
?
8. 把△ABC的每一个点横坐标都乘-1,得到△A'B'C',这一变换是( )
A.位似变换 B.旋转变换 C.中心对称变换 D.轴对称变换
?
9. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )
A.4.2米 B.4.8米 C.6.4米 D.16.8米
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 ) ?
10. 已知线段AB的长20cm,点p为AB的黄金分割点,则线段AP的长为________.
?
11. 如图,在△ABC中,D为AC边上一点,要使△CBD∽△CAB,需添加一个条件是________.
?
12. 用100倍的放大镜看一个正方形,则所看到正方形与原正方形的形状关系是________.
?
13. 已知xy=2,则x+3y2y=________.
?
14. 如图,直线l1?//?l2?//?l3,已知AG=0.6cm,BG=1.2cm,CD=1.5cm,CH=________cm.
?
15. 如图,△ABC中∠C=90?,AC=3,BC=6,D为BC中点,E是线段AB上一动点,当BE=________时△BDE∽△BAC.
?
16. 已知两数3和12,试写出第三个数,使这三个数中,其中一个数是其余两数的比例中项,第三个数是________.(只需写出一个即可).
?
17. 已知3(x+2y)=4(x-y),则x:y=________,x+yx=________.
?
18. 如图,四边形ABCD中,AD?//?BC,∠B=∠ACD=90?,AB=2,DC=3,则△ABC与△DCA的面积比为________.
?
19. 如图,在△ABC中,AB≠AC,D,E分别为边AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:________,可以使得△FDB与△ADE相似.
三、 解答题 (本题共计 7 小题 ,共计66分 ) ?
20. 如图所示,已知△ABC中,DE?//?BC,AD=2,BD=5,AC=5,求AE的长.
?
21. 如图,∠B=∠ACD.
1求证:△ABC?△ACD;
2如果AC=6,AD=4,求DB的长.
?
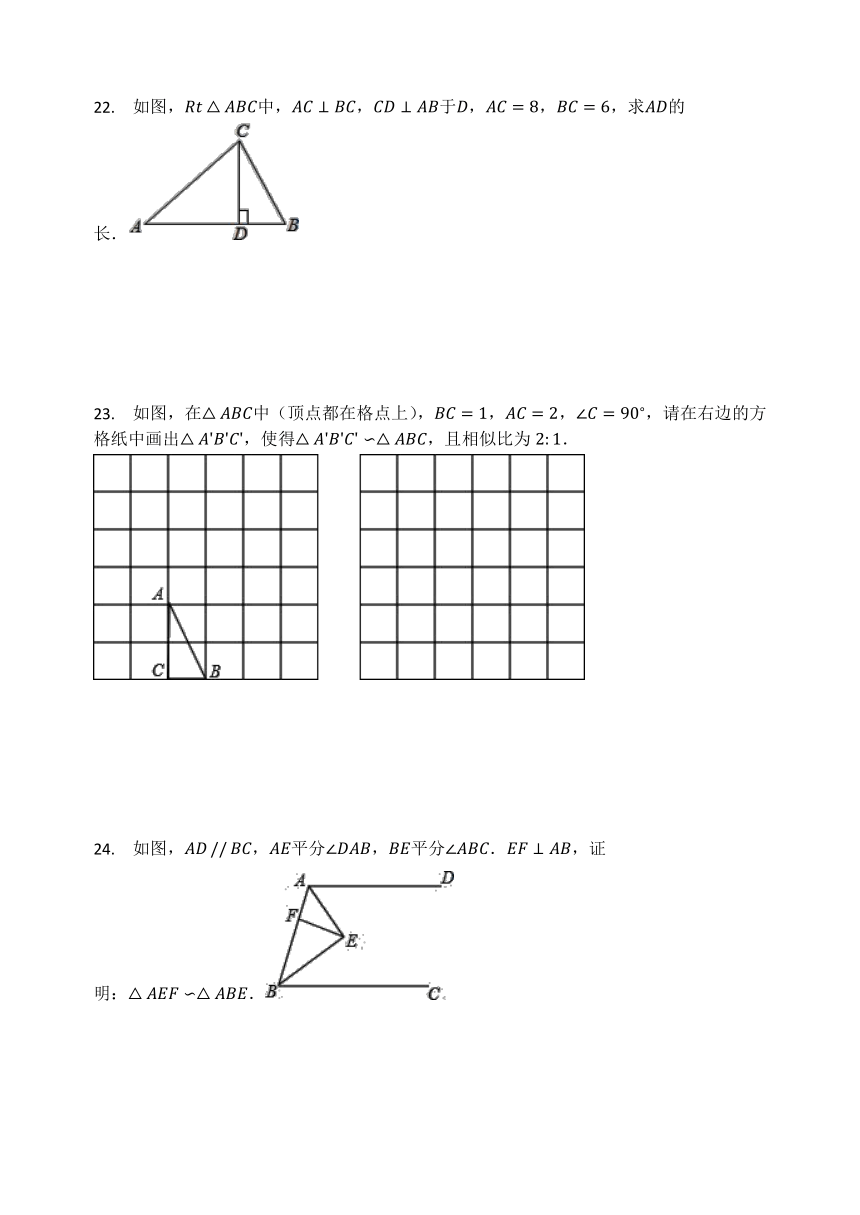
22. 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,求AD的长.
?
23. 如图,在△ABC中(顶点都在格点上),BC=1,AC=2,∠C=90?,请在右边的方格纸中画出△A'B'C',使得△A'B'C'∽△ABC,且相似比为2:1.
?
24. 如图,AD?//?BC,AE平分∠DAB,BE平分∠ABC.EF⊥AB,证明:△AEF∽△ABE.
?
25. 在等边△ABC中,D,E分别是射线BC、AB上的点,∠ADE=60?
(1)求证:△ADE∽△ABD.
(2)点D在BC延长线上,延长AC交DE于M,
①如图2,若ABAD=34,求ABBE
②如图3,点N在DE上,AD=DN且.AN交BD于点H,若BHDM=23,直接写出BEAB的值.
图1 图2
?
26. 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)
参考答案
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
1.
【答案】
C
【解答】
解:A、所有的等边三角形都相似,正确;
B、所有的等腰直角三角形都相似,正确;
C、所有的菱形不一定都相似,故错误;
D、所有的正方形都相似,正确.
故选C.
2.
【答案】
B
【解答】
解:∵ 四边形ABCD?四边形EFGH,
∴ ∠A=∠D=∠E=∠H=100?.
∵ ∠G=65?,
∴ ∠F=360?-100?-100?-65?=95?.
故选B.
3.
【答案】
B
【解答】
解:∵ DE?//?BC,
∴ ADDB=AEEC,
即63=4EC,
解得:EC=2.
故选B.
4.
【答案】
A
【解答】
解:设a3=b4=c5=k,
则a=3k,b=4k,c=5k,
则a+bb+c=3k+4k4k+5k=7k9k=79;
故选:A.
5.
【答案】
D
【解答】
∵ △DEF是由△ABC经过位似变换得到的,
∴ △DEF∽△ABC,DF?//?AC,
∴ △ODF∽△OAC,
∴ DFAC=ODOA=25,
∴ △DEF与△ABC的面积比=(25)2=4:25,
6.
【答案】
B
【解答】
解;∵ ab=bc,
∴ b2=ac=2×8=16,
∵ b>0,
∴ b=4,
故选:B.
7.
【答案】
B
【解答】
解:A、两三角形对应角相等,故相似;
B、所有的矩形的对应角相等,对应边的比不相等,故不相似;
C、所有边数相等的正多边形相似的;
D、所有的等边三角形都相似.
故选B.
8.
【答案】
D
【解答】
解:∵ 把△ABC的每一个点横坐标都乘-1,则对应点的横坐标都互为相反数,纵坐标不变,
∴ △ABC与△A'B'C'关于y轴对称.
故选D.
9.
【答案】
A
【解答】
解:过点E作EF⊥BD于点E,则∠1=∠2,
∵ ∠DEF=∠BEF=90?,
∴ ∠DEC=∠AEB,
∵ CD⊥BD,AB⊥BD,
∴ ∠CDE=∠ABE=90?,
∴ △CDE∽△ABE,
∴ DEBE=CDAB,
∵ DE=3.2米,CD=1.6米,EB=8.4米,
∴ 3.28.4=1.6AB,
解得AB=4.2(米).
故选A.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
10.
【答案】
(105-10)cm或(30-105)cm
【解答】
解:∵ P为线段AB=20cm的黄金分割点,
∴ AP=20×5-12=105-10(cm),
或AP=20×(1-5-12)=30-105(cm).
故答案为:(105-10)cm或(30-105)cm.
11.
【答案】
∠CBD=∠A
【解答】
解:添加∠CBD=∠A.
∵ ∠C=∠C,∠CBD=∠A,
∴ △CBD∽△CAB.
故答案为:∠CBD=∠A.
12.
【答案】
相似
【解答】
解:根据相似图形的定义知,用100倍的放大镜看一个正方形,则所看到正方形与原正方形的形状相同,只是大小不相同.所以所看到正方形与原正方形的形状关系是相似.
13.
【答案】
52
【解答】
解:∵ xy=2,
∴ x=2y,
∴ x+3y2y=2y+3y2y=52.
故答案为:52.
14.
【答案】
0.5
【解答】
解:∵ l1?//?l2?//?l3,
∴ AGBG=CHDH,
∵ AG=0.6cm,BG=1.2cm,CD=1.5cm,
设CH=xcm,则DH=1.5-x(cm),
∴ 0.61.2=x1.5-x,
解得:x=0.5.
即CH=0.5cm.
故答案为:0.5.
15.
【答案】
655
【解答】
解:∵ △ABC中∠C=90?,AC=3,BC=6,
∴ AB=AC2+BC2=35,
∵ D为BC中点,
∴ BD=12BC=3,
∵ ∠B=∠B,
当BDAB=BEAC时,△BDE∽△BAC,
即335=BE6,
∴ BE=655,
∴ 当BE=655时,△BDE∽△BAC.
故答案为:655.
16.
【答案】
6(答案不唯一)
【解答】
解:设第三个数是x.根据比例中项的概念,得x2=36,x=±6;或12x=9,x=34;或3x=144,x=1443,故填6(答案不唯一).
17.
【答案】
8,98
【解答】
解:∵ 3(x+2y)=4(x-y),
∴ 3x+6y=4x-2y.
∴ 6y+2y=4x-3x.
∴ 8y=x.
∴ x:y=8y:y=8.
x+yx=8y+y8y=98.
故答案为:8;98.
18.
【答案】
4:9
【解答】
∵ AD?//?BC,
∴ ∠ACB=∠DAC
又∵ ∠B=∠ACD=90?,
∴ △CBA∽△ACD,
ABCD=23,
∵ S△ABCS△DCA=(23)2=49,
∴ △ABC与△DCA的面积比为4:9.
19.
【答案】
答案不唯一,DF?//?AC,或∠BFD=∠A,或∠BDF=∠ADE等
【解答】
此题暂无解答
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
20.
【答案】
解:∵ DE?//?BC,
∴ ADAB=AEAC,即22+5=AE5,
∴ AE=107.
【解答】
解:∵ DE?//?BC,
∴ ADAB=AEAC,即22+5=AE5,
∴ AE=107.
21.
【答案】
1证明:∵ ∠A=∠A,∠ACD=∠B,
∴ △ABC?△ACD.
2∵ △ABC?△ACD,
∴ ACAD=ABAC,
∴ 64=AB6,
∴ AB=9,
∴ BD=AB-AD=9-4=5.
【解答】
1证明:∵ ∠A=∠A,∠ACD=∠B,
∴ △ABC?△ACD.
2∵ △ABC?△ACD,
∴ ACAD=ABAC,
∴ 64=AB6,
∴ AB=9,
∴ BD=AB-AD=9-4=5.
22.
【答案】
解:∵ AC⊥BC,AC=8,BC=6,
∴ AB=AC2+BC2=10,
∵ AC⊥BC,CD⊥AB,
∴ AC2=AD?AB,
∴ AD=AC2AB=6.4.
【解答】
解:∵ AC⊥BC,AC=8,BC=6,
∴ AB=AC2+BC2=10,
∵ AC⊥BC,CD⊥AB,
∴ AC2=AD?AB,
∴ AD=AC2AB=6.4.
23.
【答案】
解:
.
【解答】
解:
.
24.
【答案】
证明:∵ AE平分∠DAB,BE平分∠ABC,
∴ ∠FAE=12∠DAB,∠ABE=12∠ABC,
∵ AD?//?BC,
∴ ∠DAB+∠ABC=180?,
∴ ∠BAE+∠ABE=90?,
∴ ∠AEB=90?,
∵ EF⊥AB,
∴ ∠AFE=90?,
又∵ ∠BAE=∠BAF,
∴ △AEF∽△ABE.
【解答】
证明:∵ AE平分∠DAB,BE平分∠ABC,
∴ ∠FAE=12∠DAB,∠ABE=12∠ABC,
∵ AD?//?BC,
∴ ∠DAB+∠ABC=180?,
∴ ∠BAE+∠ABE=90?,
∴ ∠AEB=90?,
∵ EF⊥AB,
∴ ∠AFE=90?,
又∵ ∠BAE=∠BAF,
∴ △AEF∽△ABE.
25.
【答案】
1
1
【解答】
1
1
26.
【答案】
解:由题意得:∠CAD=∠MND=90?,∠CDA=MDN,
∴ △CAD?△MND,
∴ CAMN=ADND,
∴ 1.6MN=1×0.8(5+1)×0.8,
∴ MN=9.6,
又∵ ∠EBF=∠MNF=90?,
∠EFB=∠MFN,
∴ △EFB?△MFN,
∴ EBMN=BFNF,
∴ EB9.6=2×0.8(2+9)×0.8
∴ EB≈1.75,
∴ 小军身高约为1.75米.
【解答】
解:由题意得:∠CAD=∠MND=90?,∠CDA=MDN,
∴ △CAD?△MND,
∴ CAMN=ADND,
∴ 1.6MN=1×0.8(5+1)×0.8,
∴ MN=9.6,
又∵ ∠EBF=∠MNF=90?,
∠EFB=∠MFN,
∴ △EFB?△MFN,
∴ EBMN=BFNF,
∴ EB9.6=2×0.8(2+9)×0.8
∴ EB≈1.75,
∴ 小军身高约为1.75米.
(满分100分;时间:90分钟)
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
?1. 下列说法不一定正确的是( )
A.所有的等边三角形都相似 B.所有的等腰直角三角形都相似
C.所有的菱形都相似 D.所有的正方形都相似
?2. 如图,四边形ABCD?四边形EFGH,若 ∠A=∠D=100?,∠G=65?,则∠F=(? ? ? ? )
A.65? B.95? C.100? D.105?
?
3. 在△ABC中,DE?//?BC,AD=6,DB=3,AE=4,则EC的长为(? ? ? ??)
A.1 B.2 C.3 D.4
?
4. 若a3=b4=c5,则a+bb+c的值为( )
A.79 B.43 C.45 D.87
?
5. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,ODDA=23,则△DEF与△ABC的面积比为( )
A.2:3 B.4:9 C.2:5 D.4:25
?
6. 三条线段满足ab=bc,若a=2,c=8,则b的长度为( )
A.±4 B.4 C.2 D.6
?
7. 下列说法不正确的是( )
A.含30?角的直角三角形与含60?角的直角三角形是相似的
B.所有的矩形是相似的
C.所有边数相等的正多边形是相似的
D.所有的等边三角形都是相似的
?
8. 把△ABC的每一个点横坐标都乘-1,得到△A'B'C',这一变换是( )
A.位似变换 B.旋转变换 C.中心对称变换 D.轴对称变换
?
9. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )
A.4.2米 B.4.8米 C.6.4米 D.16.8米
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 ) ?
10. 已知线段AB的长20cm,点p为AB的黄金分割点,则线段AP的长为________.
?
11. 如图,在△ABC中,D为AC边上一点,要使△CBD∽△CAB,需添加一个条件是________.
?
12. 用100倍的放大镜看一个正方形,则所看到正方形与原正方形的形状关系是________.
?
13. 已知xy=2,则x+3y2y=________.
?
14. 如图,直线l1?//?l2?//?l3,已知AG=0.6cm,BG=1.2cm,CD=1.5cm,CH=________cm.
?
15. 如图,△ABC中∠C=90?,AC=3,BC=6,D为BC中点,E是线段AB上一动点,当BE=________时△BDE∽△BAC.
?
16. 已知两数3和12,试写出第三个数,使这三个数中,其中一个数是其余两数的比例中项,第三个数是________.(只需写出一个即可).
?
17. 已知3(x+2y)=4(x-y),则x:y=________,x+yx=________.
?
18. 如图,四边形ABCD中,AD?//?BC,∠B=∠ACD=90?,AB=2,DC=3,则△ABC与△DCA的面积比为________.
?
19. 如图,在△ABC中,AB≠AC,D,E分别为边AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:________,可以使得△FDB与△ADE相似.
三、 解答题 (本题共计 7 小题 ,共计66分 ) ?
20. 如图所示,已知△ABC中,DE?//?BC,AD=2,BD=5,AC=5,求AE的长.
?
21. 如图,∠B=∠ACD.
1求证:△ABC?△ACD;
2如果AC=6,AD=4,求DB的长.
?
22. 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,求AD的长.
?
23. 如图,在△ABC中(顶点都在格点上),BC=1,AC=2,∠C=90?,请在右边的方格纸中画出△A'B'C',使得△A'B'C'∽△ABC,且相似比为2:1.
?
24. 如图,AD?//?BC,AE平分∠DAB,BE平分∠ABC.EF⊥AB,证明:△AEF∽△ABE.
?
25. 在等边△ABC中,D,E分别是射线BC、AB上的点,∠ADE=60?
(1)求证:△ADE∽△ABD.
(2)点D在BC延长线上,延长AC交DE于M,
①如图2,若ABAD=34,求ABBE
②如图3,点N在DE上,AD=DN且.AN交BD于点H,若BHDM=23,直接写出BEAB的值.
图1 图2
?
26. 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)
参考答案
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
1.
【答案】
C
【解答】
解:A、所有的等边三角形都相似,正确;
B、所有的等腰直角三角形都相似,正确;
C、所有的菱形不一定都相似,故错误;
D、所有的正方形都相似,正确.
故选C.
2.
【答案】
B
【解答】
解:∵ 四边形ABCD?四边形EFGH,
∴ ∠A=∠D=∠E=∠H=100?.
∵ ∠G=65?,
∴ ∠F=360?-100?-100?-65?=95?.
故选B.
3.
【答案】
B
【解答】
解:∵ DE?//?BC,
∴ ADDB=AEEC,
即63=4EC,
解得:EC=2.
故选B.
4.
【答案】
A
【解答】
解:设a3=b4=c5=k,
则a=3k,b=4k,c=5k,
则a+bb+c=3k+4k4k+5k=7k9k=79;
故选:A.
5.
【答案】
D
【解答】
∵ △DEF是由△ABC经过位似变换得到的,
∴ △DEF∽△ABC,DF?//?AC,
∴ △ODF∽△OAC,
∴ DFAC=ODOA=25,
∴ △DEF与△ABC的面积比=(25)2=4:25,
6.
【答案】
B
【解答】
解;∵ ab=bc,
∴ b2=ac=2×8=16,
∵ b>0,
∴ b=4,
故选:B.
7.
【答案】
B
【解答】
解:A、两三角形对应角相等,故相似;
B、所有的矩形的对应角相等,对应边的比不相等,故不相似;
C、所有边数相等的正多边形相似的;
D、所有的等边三角形都相似.
故选B.
8.
【答案】
D
【解答】
解:∵ 把△ABC的每一个点横坐标都乘-1,则对应点的横坐标都互为相反数,纵坐标不变,
∴ △ABC与△A'B'C'关于y轴对称.
故选D.
9.
【答案】
A
【解答】
解:过点E作EF⊥BD于点E,则∠1=∠2,
∵ ∠DEF=∠BEF=90?,
∴ ∠DEC=∠AEB,
∵ CD⊥BD,AB⊥BD,
∴ ∠CDE=∠ABE=90?,
∴ △CDE∽△ABE,
∴ DEBE=CDAB,
∵ DE=3.2米,CD=1.6米,EB=8.4米,
∴ 3.28.4=1.6AB,
解得AB=4.2(米).
故选A.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
10.
【答案】
(105-10)cm或(30-105)cm
【解答】
解:∵ P为线段AB=20cm的黄金分割点,
∴ AP=20×5-12=105-10(cm),
或AP=20×(1-5-12)=30-105(cm).
故答案为:(105-10)cm或(30-105)cm.
11.
【答案】
∠CBD=∠A
【解答】
解:添加∠CBD=∠A.
∵ ∠C=∠C,∠CBD=∠A,
∴ △CBD∽△CAB.
故答案为:∠CBD=∠A.
12.
【答案】
相似
【解答】
解:根据相似图形的定义知,用100倍的放大镜看一个正方形,则所看到正方形与原正方形的形状相同,只是大小不相同.所以所看到正方形与原正方形的形状关系是相似.
13.
【答案】
52
【解答】
解:∵ xy=2,
∴ x=2y,
∴ x+3y2y=2y+3y2y=52.
故答案为:52.
14.
【答案】
0.5
【解答】
解:∵ l1?//?l2?//?l3,
∴ AGBG=CHDH,
∵ AG=0.6cm,BG=1.2cm,CD=1.5cm,
设CH=xcm,则DH=1.5-x(cm),
∴ 0.61.2=x1.5-x,
解得:x=0.5.
即CH=0.5cm.
故答案为:0.5.
15.
【答案】
655
【解答】
解:∵ △ABC中∠C=90?,AC=3,BC=6,
∴ AB=AC2+BC2=35,
∵ D为BC中点,
∴ BD=12BC=3,
∵ ∠B=∠B,
当BDAB=BEAC时,△BDE∽△BAC,
即335=BE6,
∴ BE=655,
∴ 当BE=655时,△BDE∽△BAC.
故答案为:655.
16.
【答案】
6(答案不唯一)
【解答】
解:设第三个数是x.根据比例中项的概念,得x2=36,x=±6;或12x=9,x=34;或3x=144,x=1443,故填6(答案不唯一).
17.
【答案】
8,98
【解答】
解:∵ 3(x+2y)=4(x-y),
∴ 3x+6y=4x-2y.
∴ 6y+2y=4x-3x.
∴ 8y=x.
∴ x:y=8y:y=8.
x+yx=8y+y8y=98.
故答案为:8;98.
18.
【答案】
4:9
【解答】
∵ AD?//?BC,
∴ ∠ACB=∠DAC
又∵ ∠B=∠ACD=90?,
∴ △CBA∽△ACD,
ABCD=23,
∵ S△ABCS△DCA=(23)2=49,
∴ △ABC与△DCA的面积比为4:9.
19.
【答案】
答案不唯一,DF?//?AC,或∠BFD=∠A,或∠BDF=∠ADE等
【解答】
此题暂无解答
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
20.
【答案】
解:∵ DE?//?BC,
∴ ADAB=AEAC,即22+5=AE5,
∴ AE=107.
【解答】
解:∵ DE?//?BC,
∴ ADAB=AEAC,即22+5=AE5,
∴ AE=107.
21.
【答案】
1证明:∵ ∠A=∠A,∠ACD=∠B,
∴ △ABC?△ACD.
2∵ △ABC?△ACD,
∴ ACAD=ABAC,
∴ 64=AB6,
∴ AB=9,
∴ BD=AB-AD=9-4=5.
【解答】
1证明:∵ ∠A=∠A,∠ACD=∠B,
∴ △ABC?△ACD.
2∵ △ABC?△ACD,
∴ ACAD=ABAC,
∴ 64=AB6,
∴ AB=9,
∴ BD=AB-AD=9-4=5.
22.
【答案】
解:∵ AC⊥BC,AC=8,BC=6,
∴ AB=AC2+BC2=10,
∵ AC⊥BC,CD⊥AB,
∴ AC2=AD?AB,
∴ AD=AC2AB=6.4.
【解答】
解:∵ AC⊥BC,AC=8,BC=6,
∴ AB=AC2+BC2=10,
∵ AC⊥BC,CD⊥AB,
∴ AC2=AD?AB,
∴ AD=AC2AB=6.4.
23.
【答案】
解:
.
【解答】
解:
.
24.
【答案】
证明:∵ AE平分∠DAB,BE平分∠ABC,
∴ ∠FAE=12∠DAB,∠ABE=12∠ABC,
∵ AD?//?BC,
∴ ∠DAB+∠ABC=180?,
∴ ∠BAE+∠ABE=90?,
∴ ∠AEB=90?,
∵ EF⊥AB,
∴ ∠AFE=90?,
又∵ ∠BAE=∠BAF,
∴ △AEF∽△ABE.
【解答】
证明:∵ AE平分∠DAB,BE平分∠ABC,
∴ ∠FAE=12∠DAB,∠ABE=12∠ABC,
∵ AD?//?BC,
∴ ∠DAB+∠ABC=180?,
∴ ∠BAE+∠ABE=90?,
∴ ∠AEB=90?,
∵ EF⊥AB,
∴ ∠AFE=90?,
又∵ ∠BAE=∠BAF,
∴ △AEF∽△ABE.
25.
【答案】
1
1
【解答】
1
1
26.
【答案】
解:由题意得:∠CAD=∠MND=90?,∠CDA=MDN,
∴ △CAD?△MND,
∴ CAMN=ADND,
∴ 1.6MN=1×0.8(5+1)×0.8,
∴ MN=9.6,
又∵ ∠EBF=∠MNF=90?,
∠EFB=∠MFN,
∴ △EFB?△MFN,
∴ EBMN=BFNF,
∴ EB9.6=2×0.8(2+9)×0.8
∴ EB≈1.75,
∴ 小军身高约为1.75米.
【解答】
解:由题意得:∠CAD=∠MND=90?,∠CDA=MDN,
∴ △CAD?△MND,
∴ CAMN=ADND,
∴ 1.6MN=1×0.8(5+1)×0.8,
∴ MN=9.6,
又∵ ∠EBF=∠MNF=90?,
∠EFB=∠MFN,
∴ △EFB?△MFN,
∴ EBMN=BFNF,
∴ EB9.6=2×0.8(2+9)×0.8
∴ EB≈1.75,
∴ 小军身高约为1.75米.
