人教版九年级数学下册 26.1 反比例函数 同步测试题(Word版有答案)
文档属性
| 名称 | 人教版九年级数学下册 26.1 反比例函数 同步测试题(Word版有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 07:47:21 | ||
图片预览


文档简介
104902001069340012319000026.1 反比例函数 同步测试题
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 已知反比例函数y=kx,当x=2时,y=-12,那么k等于( )
A.1 B.-l C.-4 D.-14
?2. 已知反比例函数y=kx的图象经过P(-2,?6),则这个函数的图象位于(? ? ? ? )
A.第二、三象限 B.第一、三象限 C.第三、四象限 D.第二、四象限
?
3. 已知反比例函数y=kx(k≠0)的图象经过点M(-2,?2),则k的值是(?????????)
A.-4 B.-1 C.1 D.4
?
4. 已知反比例函数y=2k-1x,当x<0时,y随x的增大而减小,则k的范围( )
A.k>12 B.k<12 C.k=12 D.k≠12
?
5. 如图,在同一平面直角坐标系中,反比例函数y=-kx与一次函数y=kx-3(k为常数,且k≠0)的图象可能是(? ? ? ? )
A. B.
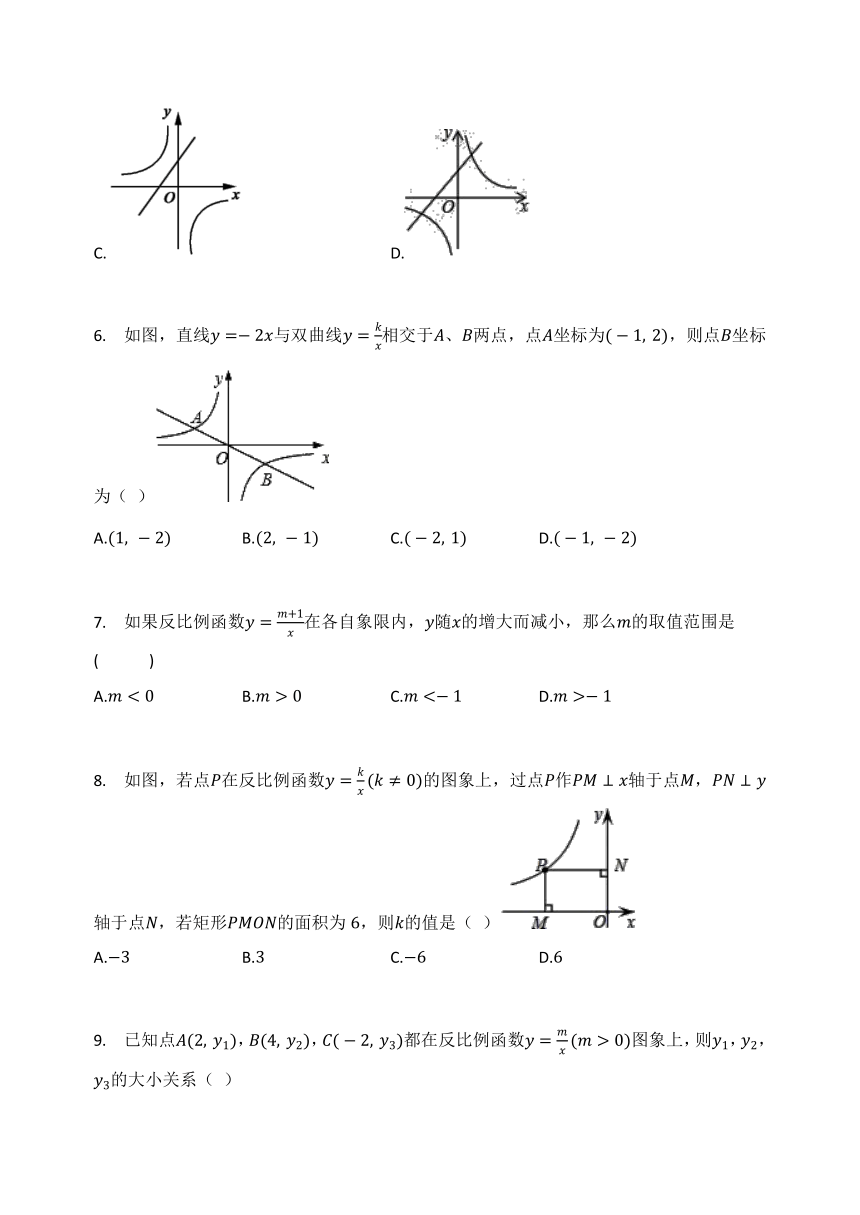
C. D.
6. 如图,直线y=-2x与双曲线y=kx相交于A、B两点,点A坐标为(-1,?2),则点B坐标为( )
A.(1,?-2) B.(2,?-1) C.(-2,?1) D.(-1,?-2)
?
7. 如果反比例函数y=m+1x在各自象限内,y随x的增大而减小,那么m的取值范围是(? ? ? ? )
A.m<0 B.m>0 C.m<-1 D.m>-1
?
8. 如图,若点P在反比例函数y=kx(k≠0)的图象上,过点P作PM⊥x轴于点M,PN⊥y轴于点N,若矩形PMON的面积为6,则k的值是( )
A.-3 B.3 C.-6 D.6
?
9. 已知点A(2,?y1),B(4,?y2),C(-2,?y3)都在反比例函数y=mx(m>0)图象上,则y1,y2,y3的大小关系( )
A.y2>y1>y3 B.y1>y2>y3 C.y3>y2>y1 D.y1>y3>y2
?
10. 如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(4a,?a)是反比例函数y=kx(k>0)的图象上与正方形的一个交点,若图中阴影部分的面积等于16,则k的值为( )
A.16 B.1 C.4 D.-16
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 已知反比例函数y=kx,当x=2时,y=-3,则k=________.
?
12. 已知反比例函数y=kx的图象经过点(-2,?-3),则k=________.
?
13. 若反比例函数y=kx的图象不经过第二象限,则k的取值范围是________.
?
14. 反比例函数的表达式为y=(m-1)xm2-2,则m=________.
?
15. 写出一个图象位于二、四象限的反比例函数的表达式,y=________.
?
16. 在平面直角坐标系xOy中,A(1,?1),B(3,?1),双曲线y=kx与线段AB有公共点,则k的取值范围是________.
?
17. 点P(2m-3,?1)在反比例函数y=1x的图象上,则m=________.
?
18. 若函数y=y1-y2,其中y1与x+1成正比例,y2与x成反比例,且当x=1和x=-1时,y的值都是-2,则当y=-5时,x的值为________.
?
19. 已知反比例函数y=2x,则当x>0时,函数值y随x增大而________(填“增大”或“减小”).
?
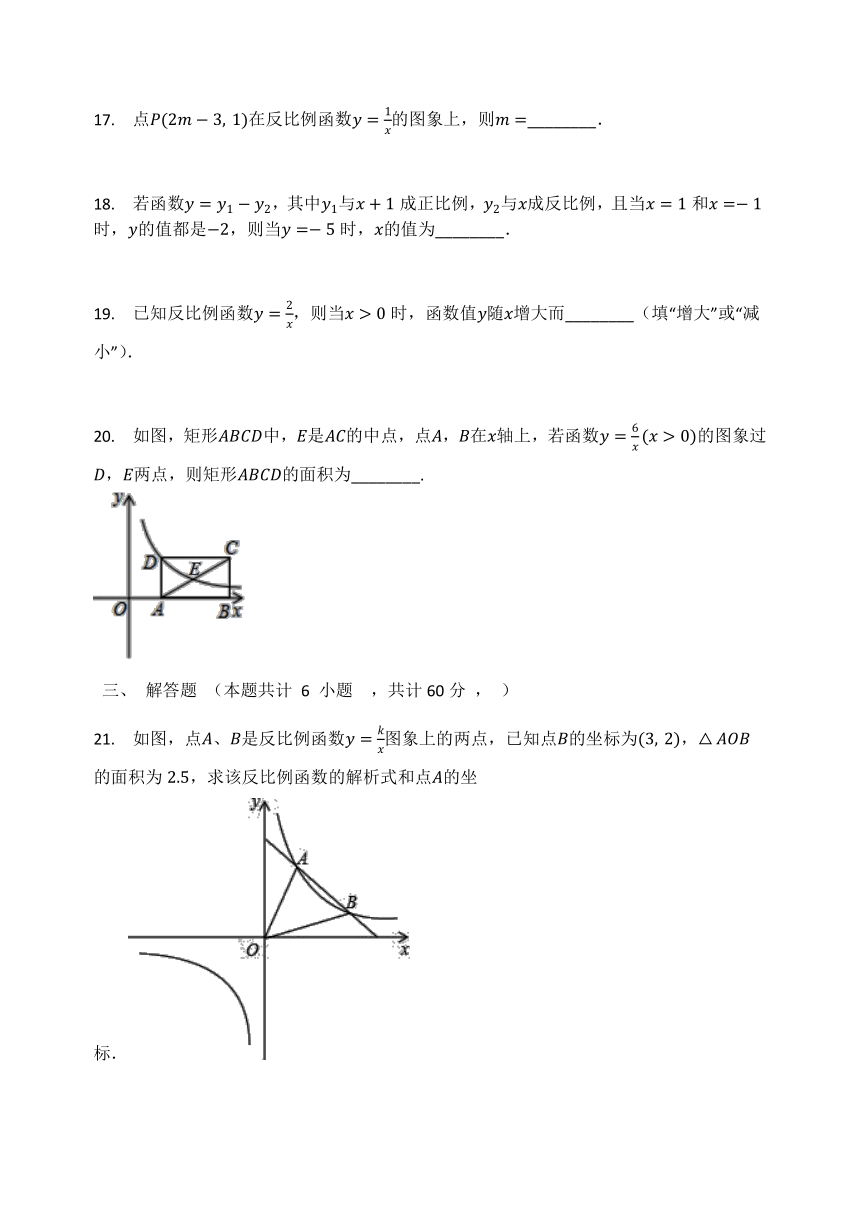
20. 如图,矩形ABCD中,E是AC的中点,点A,B在x轴上,若函数y=6x(x>0)的图象过D,E两点,则矩形ABCD的面积为________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,点A、B是反比例函数y=kx图象上的两点,已知点B的坐标为(3,?2),△AOB的面积为2.5,求该反比例函数的解析式和点A的坐标.
?
22. 在平面直角坐标系xOy中,已知:直线y=-x反比例函数y=kx的图象的一个交点为A(a,?3).
(1)试确定反比例函数的解析式;
(2)写出该反比例函数与已知直线l的另一个交点坐标.
?
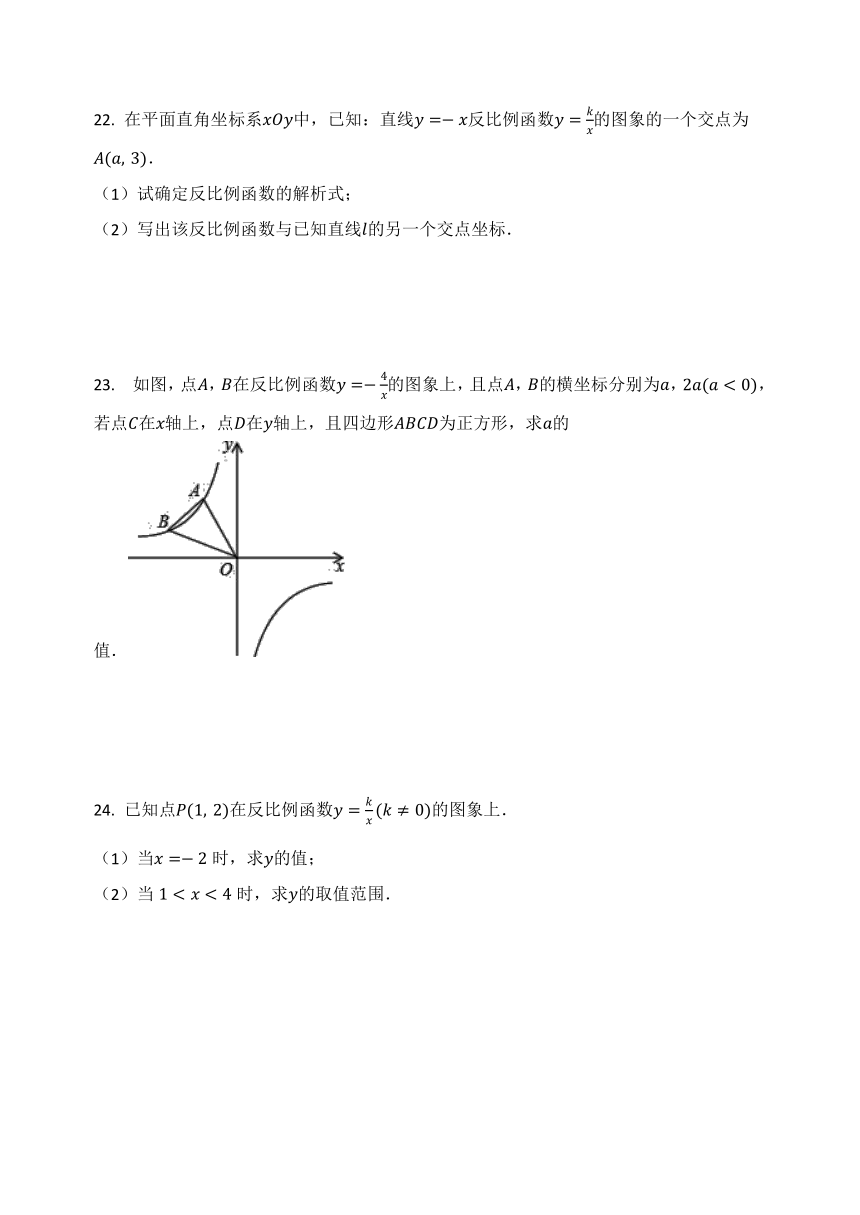
23. 如图,点A,B在反比例函数y=-4x的图象上,且点A,B的横坐标分别为a,2a(a<0),若点C在x轴上,点D在y轴上,且四边形ABCD为正方形,求a的值.
?
24. 已知点P(1,?2)在反比例函数y=kx(k≠0)的图象上.
(1)当x=-2时,求y的值;
(2)当1?
25. 在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长的数值与面积的数值相等,则点P是和谐点.
(1)判断点M(3,?6)是否为和谐点,并说明理由;
(2)若和谐点P(a,?3)(a>0)在双曲线y=kx(k为常数)上,求a,k的值.
?
26. 如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC=6.对角线AC,BD相交于点E,反比例函数y=kx(x>0)的图象经过点E,分别与AB,CD交于点F,G.
(1)若OC=8,求k的值;
(2)连接EG,若BF-BE=2,求△CEG的面积.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ 当x=2时,y=-12,
∴ -12=k2,
解得,k=-1.
故选:B.
2.
【答案】
D
【解答】
解:∵ 反比例函数y=kx的图象经过点(-2,?6),
∴ k=-12,
∵ k<0,
∴ 反比例函数的图象在第二、四象限,
故选D.
3.
【答案】
A
【解答】
解:把点M(-2,?2)代入反比例函数y=kx(k≠0)中,
得2=k-2,
∴ k=-4.
故选A.
4.
【答案】
A
【解答】
解:∵ 反比例函数y=2k-1x,当x<0时,y随x的增大而减小,
∴ 2k-1>0,
解得,k>12.
故选A.
5.
【答案】
A
【解答】
解:由一次函数图象知k>0,∴ 一次函数的图象经过第一、三、四象限,故选项C,D错误;
此时反比例函数图象分别在第二、四象限,故A选项正确,B选项错误.
故选A.
6.
【答案】
A
【解答】
解:由于点A和点B关于原点对称,点A坐标为(-1,?2),则点B坐标为(1,?-2).
故选A.
7.
【答案】
D
【解答】
解:∵ 反比例函数y=m+1x的图象在所在象限内,y的值随x值的增大而减小,
∴ m+1>0,解得m>-1.
故选D.
8.
【答案】
C
【解答】
解:设PN=a,PM=b,
则ab=6,
∵ P点在第二象限,
∴ P(-a,?b),代入y=kx中,得
k=-ab=-6,故选C.
9.
【答案】
B
【解答】
∵ 反比例函数y=mx(m>0),
∴ 函数图象的两个分式分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵ -2<2<4,
∴ 点C(-2,?y3)位于第三象限,
∴ y3<0,
∴ A(2,?y1)和B(4,?y2)位于第一象限,
∴ y1>0,y2>0,
∵ 2<4,
∴ y1>y2,
∴ y1>y2>y3.
10.
【答案】
C
【解答】
解:∵ 图中阴影部分的面积等于16,
∴ 正方形OABC的面积=16,
∵ P点坐标为(4a,?a),
∴ 4a×4a=16,
∴ a=1(a=-1舍去),
∴ P点坐标为(4,?1),
把P(4,?1)代入y=kx,得
k=4×1=4.
故选:C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
-6
【解答】
解:把x=2,y=-3代入y=kx得:k2=-3,
解得:k=-6.
故答案是:-6.
12.
【答案】
6
【解答】
解:由y=kx,得
k=xy,
∵ 反比例函数y=kx的图象经过点(-2,?-3),
∴ k=(-2)×(-3)=6.
故答案是:6.
13.
【答案】
k>0
【解答】
反比例函数y=kx的图象不经过第二象限,
则经过一三象限,
∴ k>0.
14.
【答案】
-1
【解答】
解:依题意有m2-2=-1且(m-1)≠0,所以m=-1.
故答案为:-1.
15.
【答案】
答案不唯一,如y=-1x等
【解答】
解:根据反比例函数的性质,其图象位于第二、四象限,则其系数k<0;
故只要给出k小于0的反比例函数即可;答案不唯一,如y=-1x等.
16.
【答案】
1≤k≤3
【解答】
解:当(1,?1)在y=kx上时,k=1,
当(3,?1)在y=kx的图象上时,k=3.
若双曲线y=kx与线段AB有公共点,则k的取值范围是1≤k≤3.
故答案为:1≤k≤3.
17.
【答案】
2
【解答】
解:∵ 点P(2m-3,?1)在反比例函数y=1x的图象上,∴ (2m-3)×1=1,解得m=2.
故答案为:2.
18.
【答案】
-12或2
【解答】
解:∵ y1与x+1成正比例,
∴ y=k1(x+1).
∵ y2与x成反比例,
∴ y2=k2x.
y=k1(x+1)-k2x.
当x=±1时,y=-2;
∴ 2k1-k2=-2k2=-2
解得:k1=-2k2=-2,
∴ y=-2(x+1)+2x.
当x=-5时,-5=-2(x+1)+2x,
解得x=-12或x=2
故答案为-12或2.
19.
【答案】
减小
【解答】
解:∵ k=2>0,
∴ 图象在第一、三象限,且在每一个象限y随x的增大而减小.
故答案为:减小.
20.
【答案】
12
【解答】
解:过E作EF⊥AB于F,如图,
∵ 点E是矩形ABCD对角线的交点,
∴ AE=CE,
∴ EF是△ABC的中位线,
∴ AD=2EF.
设点D的横坐标为m,且点D在反比例函数y=6x(x>0)上,
∴ D点坐标为(m,?6m),
∴ AD=6m,
∴ EF=3m,
∴ E(2m,?3m),
∴ AF=m,
∴ AB=2m,
∴ 矩形ABCD的面积=2m?6m=12.
故答案为:12.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:把点B的坐标(3,?2)代入y=kx,得
k=xy=3×2=6,
则该反比例函数为解析式为:y=6x.
如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
设A(a,?6a).
∵ 点A、B是反比例函数y=kx图象上的两点,
∴ S△AOC=S△BOD,
∴ S△AOB=S△AOC+S梯形ACDB-S△BOD=S梯形ACDB,
则2.5=2+6a2×(3-a),
整理,得
(a-2)(a+9)=0,
解得a1=2,a2=-9(舍去).
则A(2,?3).
综上所述,该反比例函数的解析式是y=6x,点A的坐标是(2,?3).
【解答】
解:把点B的坐标(3,?2)代入y=kx,得
k=xy=3×2=6,
则该反比例函数为解析式为:y=6x.
如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
设A(a,?6a).
∵ 点A、B是反比例函数y=kx图象上的两点,
∴ S△AOC=S△BOD,
∴ S△AOB=S△AOC+S梯形ACDB-S△BOD=S梯形ACDB,
则2.5=2+6a2×(3-a),
整理,得
(a-2)(a+9)=0,
解得a1=2,a2=-9(舍去).
则A(2,?3).
综上所述,该反比例函数的解析式是y=6x,点A的坐标是(2,?3).
22.
【答案】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
【解答】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
23.
【答案】
解:作BE⊥x轴于E,AF⊥y轴于F,
∵ 四边形ABCD是正方形,
∴ AB=BC=CD=DA,∠A=∠B=∠C=∠D=90?,
∴ ∠BCE=∠CDO=∠DAF,
在△BEC和△COD和△DFA中,
∠BCE=∠CDO=∠DAF∠BEC=∠COD=∠DFABC=CD=DA,
∴ △BEC?△COD?△DFA,
∴ BE=CO=DF,EC=OD=AF,
∵ 点A,B的横坐标分别为a,2a(a<0),
∴ EC=OD=AF=-a,EC+OC=-2a,
∴ BE=CO=DF=-a,
∴ B(2a,?-a),
∵ 点B在反比例函数y=-4x的图象上,
∴ -a=-42a,解得,a=-2.
【解答】
解:作BE⊥x轴于E,AF⊥y轴于F,
∵ 四边形ABCD是正方形,
∴ AB=BC=CD=DA,∠A=∠B=∠C=∠D=90?,
∴ ∠BCE=∠CDO=∠DAF,
在△BEC和△COD和△DFA中,
∠BCE=∠CDO=∠DAF∠BEC=∠COD=∠DFABC=CD=DA,
∴ △BEC?△COD?△DFA,
∴ BE=CO=DF,EC=OD=AF,
∵ 点A,B的横坐标分别为a,2a(a<0),
∴ EC=OD=AF=-a,EC+OC=-2a,
∴ BE=CO=DF=-a,
∴ B(2a,?-a),
∵ 点B在反比例函数y=-4x的图象上,
∴ -a=-42a,解得,a=-2.
24.
【答案】
解:(1)∵ 点P(1,?2)在反比例函数y=kx的图象上,
∴ 2=k1,
∴ k=2,
∴ y=2x,
当x=-2时,y=2-2=-1;
(2)∵ 当x=1时,y=2;当x=4时,y=12;
又∵ 反比例函数y=2x在x>0时,y值随x的增大而减小,
∴ 当1【解答】
解:(1)∵ 点P(1,?2)在反比例函数y=kx的图象上,
∴ 2=k1,
∴ k=2,
∴ y=2x,
当x=-2时,y=2-2=-1;
(2)∵ 当x=1时,y=2;当x=4时,y=12;
又∵ 反比例函数y=2x在x>0时,y值随x的增大而减小,
∴ 当125.
【答案】
解:(1)∵ 点M(3,?6),
∴ 矩形OAPB的周长=2(3+6)=18,
面积=3×6=18,
∵ 18=18,
∴ 则点P是和谐点;
(2)∵ 点P(a,?3),
∴ 矩形OAPB的周长=2(a+3),
面积=3a,
∵ 点P是和谐点.
∴ 2(a+3)=3a,
解得a=6,
所以,点P(6,?3),
∵ 点P在双曲线y=kx上,
∴ k6=3,
解得k=18.
【解答】
解:(1)∵ 点M(3,?6),
∴ 矩形OAPB的周长=2(3+6)=18,
面积=3×6=18,
∵ 18=18,
∴ 则点P是和谐点;
(2)∵ 点P(a,?3),
∴ 矩形OAPB的周长=2(a+3),
面积=3a,
∵ 点P是和谐点.
∴ 2(a+3)=3a,
解得a=6,
所以,点P(6,?3),
∵ 点P在双曲线y=kx上,
∴ k6=3,
解得k=18.
26.
【答案】
∵ 在矩形ABCD的顶点B,AB=8,BC=6,
而OC=8,
∴ B(2,?0),A(2,?8),C(8,?0),
∵ 对角线AC,BD相交于点E,
∴ 点E为AC的中点,
∴ E(5,?4),
把E(5,?4)代入y=kx得k=5×4=20;
∵ AC=62+82=10,
∴ BE=EC=5,
∵ BF-BE=2,
∴ BF=7,
设OB=t,则F(t,?7),E(t+3,?4),
∵ 反比例函数y=kx(x>0)的图象经过点E、F,
∴ 7t=4(t+3),解得t=4,
∴ k=7t=28,
∴ 反比例函数解析式为y=28x,
当x=10时,y=2810=145,
∴ G(10,?145),
∴ △CEG的面积=12×3×145=215.
【解答】
∵ 在矩形ABCD的顶点B,AB=8,BC=6,
而OC=8,
∴ B(2,?0),A(2,?8),C(8,?0),
∵ 对角线AC,BD相交于点E,
∴ 点E为AC的中点,
∴ E(5,?4),
把E(5,?4)代入y=kx得k=5×4=20;
∵ AC=62+82=10,
∴ BE=EC=5,
∵ BF-BE=2,
∴ BF=7,
设OB=t,则F(t,?7),E(t+3,?4),
∵ 反比例函数y=kx(x>0)的图象经过点E、F,
∴ 7t=4(t+3),解得t=4,
∴ k=7t=28,
∴ 反比例函数解析式为y=28x,
当x=10时,y=2810=145,
∴ G(10,?145),
∴ △CEG的面积=12×3×145=215.
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 已知反比例函数y=kx,当x=2时,y=-12,那么k等于( )
A.1 B.-l C.-4 D.-14
?2. 已知反比例函数y=kx的图象经过P(-2,?6),则这个函数的图象位于(? ? ? ? )
A.第二、三象限 B.第一、三象限 C.第三、四象限 D.第二、四象限
?
3. 已知反比例函数y=kx(k≠0)的图象经过点M(-2,?2),则k的值是(?????????)
A.-4 B.-1 C.1 D.4
?
4. 已知反比例函数y=2k-1x,当x<0时,y随x的增大而减小,则k的范围( )
A.k>12 B.k<12 C.k=12 D.k≠12
?
5. 如图,在同一平面直角坐标系中,反比例函数y=-kx与一次函数y=kx-3(k为常数,且k≠0)的图象可能是(? ? ? ? )
A. B.
C. D.
6. 如图,直线y=-2x与双曲线y=kx相交于A、B两点,点A坐标为(-1,?2),则点B坐标为( )
A.(1,?-2) B.(2,?-1) C.(-2,?1) D.(-1,?-2)
?
7. 如果反比例函数y=m+1x在各自象限内,y随x的增大而减小,那么m的取值范围是(? ? ? ? )
A.m<0 B.m>0 C.m<-1 D.m>-1
?
8. 如图,若点P在反比例函数y=kx(k≠0)的图象上,过点P作PM⊥x轴于点M,PN⊥y轴于点N,若矩形PMON的面积为6,则k的值是( )
A.-3 B.3 C.-6 D.6
?
9. 已知点A(2,?y1),B(4,?y2),C(-2,?y3)都在反比例函数y=mx(m>0)图象上,则y1,y2,y3的大小关系( )
A.y2>y1>y3 B.y1>y2>y3 C.y3>y2>y1 D.y1>y3>y2
?
10. 如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(4a,?a)是反比例函数y=kx(k>0)的图象上与正方形的一个交点,若图中阴影部分的面积等于16,则k的值为( )
A.16 B.1 C.4 D.-16
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 已知反比例函数y=kx,当x=2时,y=-3,则k=________.
?
12. 已知反比例函数y=kx的图象经过点(-2,?-3),则k=________.
?
13. 若反比例函数y=kx的图象不经过第二象限,则k的取值范围是________.
?
14. 反比例函数的表达式为y=(m-1)xm2-2,则m=________.
?
15. 写出一个图象位于二、四象限的反比例函数的表达式,y=________.
?
16. 在平面直角坐标系xOy中,A(1,?1),B(3,?1),双曲线y=kx与线段AB有公共点,则k的取值范围是________.
?
17. 点P(2m-3,?1)在反比例函数y=1x的图象上,则m=________.
?
18. 若函数y=y1-y2,其中y1与x+1成正比例,y2与x成反比例,且当x=1和x=-1时,y的值都是-2,则当y=-5时,x的值为________.
?
19. 已知反比例函数y=2x,则当x>0时,函数值y随x增大而________(填“增大”或“减小”).
?
20. 如图,矩形ABCD中,E是AC的中点,点A,B在x轴上,若函数y=6x(x>0)的图象过D,E两点,则矩形ABCD的面积为________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,点A、B是反比例函数y=kx图象上的两点,已知点B的坐标为(3,?2),△AOB的面积为2.5,求该反比例函数的解析式和点A的坐标.
?
22. 在平面直角坐标系xOy中,已知:直线y=-x反比例函数y=kx的图象的一个交点为A(a,?3).
(1)试确定反比例函数的解析式;
(2)写出该反比例函数与已知直线l的另一个交点坐标.
?
23. 如图,点A,B在反比例函数y=-4x的图象上,且点A,B的横坐标分别为a,2a(a<0),若点C在x轴上,点D在y轴上,且四边形ABCD为正方形,求a的值.
?
24. 已知点P(1,?2)在反比例函数y=kx(k≠0)的图象上.
(1)当x=-2时,求y的值;
(2)当1
25. 在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长的数值与面积的数值相等,则点P是和谐点.
(1)判断点M(3,?6)是否为和谐点,并说明理由;
(2)若和谐点P(a,?3)(a>0)在双曲线y=kx(k为常数)上,求a,k的值.
?
26. 如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC=6.对角线AC,BD相交于点E,反比例函数y=kx(x>0)的图象经过点E,分别与AB,CD交于点F,G.
(1)若OC=8,求k的值;
(2)连接EG,若BF-BE=2,求△CEG的面积.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ 当x=2时,y=-12,
∴ -12=k2,
解得,k=-1.
故选:B.
2.
【答案】
D
【解答】
解:∵ 反比例函数y=kx的图象经过点(-2,?6),
∴ k=-12,
∵ k<0,
∴ 反比例函数的图象在第二、四象限,
故选D.
3.
【答案】
A
【解答】
解:把点M(-2,?2)代入反比例函数y=kx(k≠0)中,
得2=k-2,
∴ k=-4.
故选A.
4.
【答案】
A
【解答】
解:∵ 反比例函数y=2k-1x,当x<0时,y随x的增大而减小,
∴ 2k-1>0,
解得,k>12.
故选A.
5.
【答案】
A
【解答】
解:由一次函数图象知k>0,∴ 一次函数的图象经过第一、三、四象限,故选项C,D错误;
此时反比例函数图象分别在第二、四象限,故A选项正确,B选项错误.
故选A.
6.
【答案】
A
【解答】
解:由于点A和点B关于原点对称,点A坐标为(-1,?2),则点B坐标为(1,?-2).
故选A.
7.
【答案】
D
【解答】
解:∵ 反比例函数y=m+1x的图象在所在象限内,y的值随x值的增大而减小,
∴ m+1>0,解得m>-1.
故选D.
8.
【答案】
C
【解答】
解:设PN=a,PM=b,
则ab=6,
∵ P点在第二象限,
∴ P(-a,?b),代入y=kx中,得
k=-ab=-6,故选C.
9.
【答案】
B
【解答】
∵ 反比例函数y=mx(m>0),
∴ 函数图象的两个分式分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵ -2<2<4,
∴ 点C(-2,?y3)位于第三象限,
∴ y3<0,
∴ A(2,?y1)和B(4,?y2)位于第一象限,
∴ y1>0,y2>0,
∵ 2<4,
∴ y1>y2,
∴ y1>y2>y3.
10.
【答案】
C
【解答】
解:∵ 图中阴影部分的面积等于16,
∴ 正方形OABC的面积=16,
∵ P点坐标为(4a,?a),
∴ 4a×4a=16,
∴ a=1(a=-1舍去),
∴ P点坐标为(4,?1),
把P(4,?1)代入y=kx,得
k=4×1=4.
故选:C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
-6
【解答】
解:把x=2,y=-3代入y=kx得:k2=-3,
解得:k=-6.
故答案是:-6.
12.
【答案】
6
【解答】
解:由y=kx,得
k=xy,
∵ 反比例函数y=kx的图象经过点(-2,?-3),
∴ k=(-2)×(-3)=6.
故答案是:6.
13.
【答案】
k>0
【解答】
反比例函数y=kx的图象不经过第二象限,
则经过一三象限,
∴ k>0.
14.
【答案】
-1
【解答】
解:依题意有m2-2=-1且(m-1)≠0,所以m=-1.
故答案为:-1.
15.
【答案】
答案不唯一,如y=-1x等
【解答】
解:根据反比例函数的性质,其图象位于第二、四象限,则其系数k<0;
故只要给出k小于0的反比例函数即可;答案不唯一,如y=-1x等.
16.
【答案】
1≤k≤3
【解答】
解:当(1,?1)在y=kx上时,k=1,
当(3,?1)在y=kx的图象上时,k=3.
若双曲线y=kx与线段AB有公共点,则k的取值范围是1≤k≤3.
故答案为:1≤k≤3.
17.
【答案】
2
【解答】
解:∵ 点P(2m-3,?1)在反比例函数y=1x的图象上,∴ (2m-3)×1=1,解得m=2.
故答案为:2.
18.
【答案】
-12或2
【解答】
解:∵ y1与x+1成正比例,
∴ y=k1(x+1).
∵ y2与x成反比例,
∴ y2=k2x.
y=k1(x+1)-k2x.
当x=±1时,y=-2;
∴ 2k1-k2=-2k2=-2
解得:k1=-2k2=-2,
∴ y=-2(x+1)+2x.
当x=-5时,-5=-2(x+1)+2x,
解得x=-12或x=2
故答案为-12或2.
19.
【答案】
减小
【解答】
解:∵ k=2>0,
∴ 图象在第一、三象限,且在每一个象限y随x的增大而减小.
故答案为:减小.
20.
【答案】
12
【解答】
解:过E作EF⊥AB于F,如图,
∵ 点E是矩形ABCD对角线的交点,
∴ AE=CE,
∴ EF是△ABC的中位线,
∴ AD=2EF.
设点D的横坐标为m,且点D在反比例函数y=6x(x>0)上,
∴ D点坐标为(m,?6m),
∴ AD=6m,
∴ EF=3m,
∴ E(2m,?3m),
∴ AF=m,
∴ AB=2m,
∴ 矩形ABCD的面积=2m?6m=12.
故答案为:12.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:把点B的坐标(3,?2)代入y=kx,得
k=xy=3×2=6,
则该反比例函数为解析式为:y=6x.
如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
设A(a,?6a).
∵ 点A、B是反比例函数y=kx图象上的两点,
∴ S△AOC=S△BOD,
∴ S△AOB=S△AOC+S梯形ACDB-S△BOD=S梯形ACDB,
则2.5=2+6a2×(3-a),
整理,得
(a-2)(a+9)=0,
解得a1=2,a2=-9(舍去).
则A(2,?3).
综上所述,该反比例函数的解析式是y=6x,点A的坐标是(2,?3).
【解答】
解:把点B的坐标(3,?2)代入y=kx,得
k=xy=3×2=6,
则该反比例函数为解析式为:y=6x.
如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
设A(a,?6a).
∵ 点A、B是反比例函数y=kx图象上的两点,
∴ S△AOC=S△BOD,
∴ S△AOB=S△AOC+S梯形ACDB-S△BOD=S梯形ACDB,
则2.5=2+6a2×(3-a),
整理,得
(a-2)(a+9)=0,
解得a1=2,a2=-9(舍去).
则A(2,?3).
综上所述,该反比例函数的解析式是y=6x,点A的坐标是(2,?3).
22.
【答案】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
【解答】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
23.
【答案】
解:作BE⊥x轴于E,AF⊥y轴于F,
∵ 四边形ABCD是正方形,
∴ AB=BC=CD=DA,∠A=∠B=∠C=∠D=90?,
∴ ∠BCE=∠CDO=∠DAF,
在△BEC和△COD和△DFA中,
∠BCE=∠CDO=∠DAF∠BEC=∠COD=∠DFABC=CD=DA,
∴ △BEC?△COD?△DFA,
∴ BE=CO=DF,EC=OD=AF,
∵ 点A,B的横坐标分别为a,2a(a<0),
∴ EC=OD=AF=-a,EC+OC=-2a,
∴ BE=CO=DF=-a,
∴ B(2a,?-a),
∵ 点B在反比例函数y=-4x的图象上,
∴ -a=-42a,解得,a=-2.
【解答】
解:作BE⊥x轴于E,AF⊥y轴于F,
∵ 四边形ABCD是正方形,
∴ AB=BC=CD=DA,∠A=∠B=∠C=∠D=90?,
∴ ∠BCE=∠CDO=∠DAF,
在△BEC和△COD和△DFA中,
∠BCE=∠CDO=∠DAF∠BEC=∠COD=∠DFABC=CD=DA,
∴ △BEC?△COD?△DFA,
∴ BE=CO=DF,EC=OD=AF,
∵ 点A,B的横坐标分别为a,2a(a<0),
∴ EC=OD=AF=-a,EC+OC=-2a,
∴ BE=CO=DF=-a,
∴ B(2a,?-a),
∵ 点B在反比例函数y=-4x的图象上,
∴ -a=-42a,解得,a=-2.
24.
【答案】
解:(1)∵ 点P(1,?2)在反比例函数y=kx的图象上,
∴ 2=k1,
∴ k=2,
∴ y=2x,
当x=-2时,y=2-2=-1;
(2)∵ 当x=1时,y=2;当x=4时,y=12;
又∵ 反比例函数y=2x在x>0时,y值随x的增大而减小,
∴ 当1
解:(1)∵ 点P(1,?2)在反比例函数y=kx的图象上,
∴ 2=k1,
∴ k=2,
∴ y=2x,
当x=-2时,y=2-2=-1;
(2)∵ 当x=1时,y=2;当x=4时,y=12;
又∵ 反比例函数y=2x在x>0时,y值随x的增大而减小,
∴ 当1
【答案】
解:(1)∵ 点M(3,?6),
∴ 矩形OAPB的周长=2(3+6)=18,
面积=3×6=18,
∵ 18=18,
∴ 则点P是和谐点;
(2)∵ 点P(a,?3),
∴ 矩形OAPB的周长=2(a+3),
面积=3a,
∵ 点P是和谐点.
∴ 2(a+3)=3a,
解得a=6,
所以,点P(6,?3),
∵ 点P在双曲线y=kx上,
∴ k6=3,
解得k=18.
【解答】
解:(1)∵ 点M(3,?6),
∴ 矩形OAPB的周长=2(3+6)=18,
面积=3×6=18,
∵ 18=18,
∴ 则点P是和谐点;
(2)∵ 点P(a,?3),
∴ 矩形OAPB的周长=2(a+3),
面积=3a,
∵ 点P是和谐点.
∴ 2(a+3)=3a,
解得a=6,
所以,点P(6,?3),
∵ 点P在双曲线y=kx上,
∴ k6=3,
解得k=18.
26.
【答案】
∵ 在矩形ABCD的顶点B,AB=8,BC=6,
而OC=8,
∴ B(2,?0),A(2,?8),C(8,?0),
∵ 对角线AC,BD相交于点E,
∴ 点E为AC的中点,
∴ E(5,?4),
把E(5,?4)代入y=kx得k=5×4=20;
∵ AC=62+82=10,
∴ BE=EC=5,
∵ BF-BE=2,
∴ BF=7,
设OB=t,则F(t,?7),E(t+3,?4),
∵ 反比例函数y=kx(x>0)的图象经过点E、F,
∴ 7t=4(t+3),解得t=4,
∴ k=7t=28,
∴ 反比例函数解析式为y=28x,
当x=10时,y=2810=145,
∴ G(10,?145),
∴ △CEG的面积=12×3×145=215.
【解答】
∵ 在矩形ABCD的顶点B,AB=8,BC=6,
而OC=8,
∴ B(2,?0),A(2,?8),C(8,?0),
∵ 对角线AC,BD相交于点E,
∴ 点E为AC的中点,
∴ E(5,?4),
把E(5,?4)代入y=kx得k=5×4=20;
∵ AC=62+82=10,
∴ BE=EC=5,
∵ BF-BE=2,
∴ BF=7,
设OB=t,则F(t,?7),E(t+3,?4),
∵ 反比例函数y=kx(x>0)的图象经过点E、F,
∴ 7t=4(t+3),解得t=4,
∴ k=7t=28,
∴ 反比例函数解析式为y=28x,
当x=10时,y=2810=145,
∴ G(10,?145),
∴ △CEG的面积=12×3×145=215.
