北师大版 七年级下册数学 1.6 完全平方公式 同步测试 (Word版 含解析)
文档属性
| 名称 | 北师大版 七年级下册数学 1.6 完全平方公式 同步测试 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 68.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 07:22:21 | ||
图片预览


文档简介
1.6完全平方公式 同步测试
一.选择题
1.下列代数式不是完全平方式的是( )
A.112mn+49m2+64n2 B.4m2+20mn+25n2
C.m2n2+2mn+4 D.m2+16m+64
2.下列等式一定成立的是( )
A.a2+a2=a5 B.(a+b)2=a2+b2
C.(2ab2)3=6a3b4 D.(x﹣a)(x﹣a)=x2﹣2ax+a2
3.如果x2+6xy+m是一个完全平方式,则m的值为( )
A.9y2 B.3y2 C.y2 D.6y2
4.若x2+y2=(x+y)2+A=(x﹣y)2﹣B,则A、B的数量关系为( )
A.相等 B.互为相反数 C.互为倒数 D.无法确定
5.计算(x﹣2)(2x+3)﹣(3x+1)2的结果中,x项的系数为( )
A.5 B.﹣5 C.7 D.﹣7
6.若25x2+kxy+4y2是完全平方公式,则k的值为( )
A.10或﹣20 B.﹣20 或20 C.5或﹣5 D.10或﹣10
7.若x2+2(m﹣5)x+16是完全平方式,则m的值是( )
A.5 B.9 C.9或1 D.5或1
8.小淇将(2019x+2020)2展开后得到a1x2+b1x+c1;小尧将(2020x﹣2019)2展开后得到a2x2+b2x+c2,若两人计算过程无误,则a1﹣a2的值为( )
A.﹣1 B.﹣4039 C.4039 D.1
9.若长方形的周长为36,其中一边长为x(x>0),面积为y,则y与x之间的关系为( )
A.y=(18﹣x)x B.y=x2 C.y=(36﹣x)x D.y=(18﹣x)2
10.如图,在边长为a+b的正方形的四个角上,分别剪去直角边长分别为a,b的四个直角三角形,则剩余部分面积,即图中的阴影部分的面积是( )
A.a2﹣b2 B.2ab C.a2+b2 D.4ab
二.填空题
11.代数式4x2+2(m﹣1)x+9是完全平方式,则m= .
12.若ab=﹣2,a2+b2=5,则(a﹣b)2的值为 .
13.以下四个结论正确的是 .(填序号)
①若(x﹣1)x+1=1,则x只能是2
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,则a=﹣1
③若a+b=10,ab=24,则a﹣b=2或a﹣b=﹣2
④若4x=a,8y=b,则22x﹣3y可表示为
14.如图1中的小长方形的长为x,宽为y,将四个同样的小长方形拼成如图2所示的正方形,则小长方形的面积为 .
15.如图所示,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么阴影部分的面积是 .
三.解答题
16.用简便方法计算(结果用科学记数法表示):
(1)0.259×220×259×643;
(2)20012﹣4002+1.
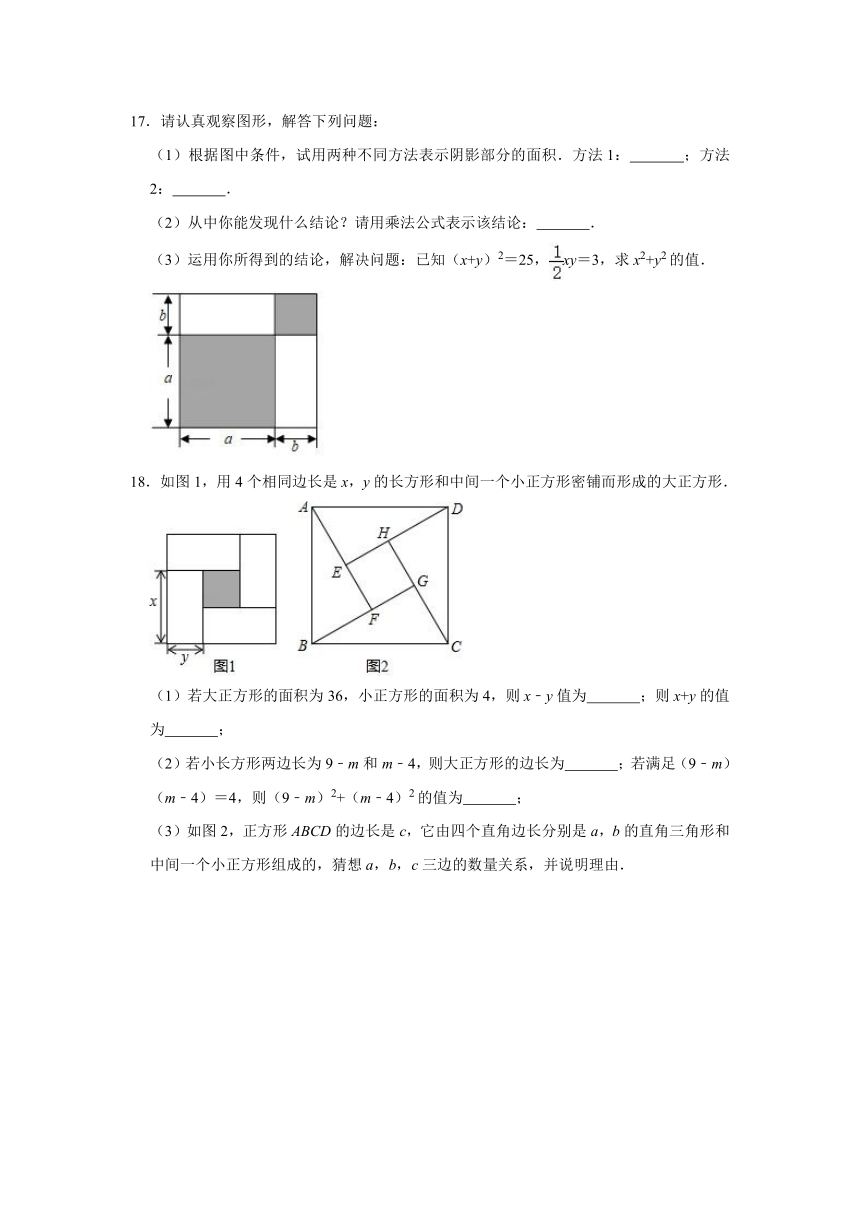
17.请认真观察图形,解答下列问题:
(1)根据图中条件,试用两种不同方法表示阴影部分的面积.方法1: ;方法2: .
(2)从中你能发现什么结论?请用乘法公式表示该结论: .
(3)运用你所得到的结论,解决问题:已知(x+y)2=25,xy=3,求x2+y2的值.
18.如图1,用4个相同边长是x,y的长方形和中间一个小正方形密铺而形成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则x﹣y值为 ;则x+y的值为 ;
(2)若小长方形两边长为9﹣m和m﹣4,则大正方形的边长为 ;若满足(9﹣m)(m﹣4)=4,则(9﹣m)2+(m﹣4)2的值为 ;
(3)如图2,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,猜想a,b,c三边的数量关系,并说明理由.
参考答案
一.选择题
1.解:A、原式=(7m+8n)2,故本选项不符合题意.
B、原式=(2m+5n)2,故本选项不符合题意.
C、该代数式不是完全平方式,故本选项符合题意.
D、原式=(m+8)2,故本选项不符合题意.
故选:C.
2.解:A、原式=2a2,所以A选项错误;
B、原式=a2+2ab+b2,所以B选项错误;
C、原式=8a2b6,所以C选项错误;
D、原式=(x﹣a)2=x2﹣2ax+a2,所以D选项正确.
故选:D.
3.解:∵x2+6xy+m是一个完全平方式,
∴m==9y2.
故选:A.
4.解:∵x2+y2=(x+y)2+(﹣2xy)=(x﹣y)2﹣(﹣2xy),
∴A=﹣2xy,B=﹣2xy,
∴A=B.
故选:A.
5.解:(x﹣2)(2x+3)﹣(3x+1)2
=2x2+3x﹣4x﹣6﹣9x2﹣6x﹣1
=﹣7x2﹣7x﹣7,
故选:D.
6.解:∵25x2+kxy+4y2是完全平方公式,
∴k=±2×5×2=±20,
故选:B.
7.解:∵x2+2(m﹣5)x+16是完全平方式,
∴m﹣5=±4,
解得:m=9或1,
则m的值是9或1.
故选:C.
8.解:∵(2019x+2020)2展开后得到a1x2+b1x+c1;
∴a1=20192,
∵(2020x﹣2019)2展开后得到a2x2+b2x+c2,
∴a2=20202,
∴a1﹣a2=20192﹣20202=(2019+2020)(2019﹣2020)=﹣4039,
故选:B.
9.解:长方形的周长为36,其中一边长为x(x>0),则另一边长为
36÷2﹣x=18﹣x,
∴y=x(18﹣x)
故选:A.
10.解:由题意得,S阴影部分=S正方形﹣4S三角形=(a+b)2﹣ab×4=a2+2ab+b2﹣2ab═a2+b2,
故选:C.
二.填空题
11.解:∵(2x±3)2=4x2±12x+9,
∴2(m﹣1)=±12,
∴m﹣1=±6,
∴m=7或m=﹣5.
故答案为:7或﹣5.
12.解:∵ab=﹣2,a2+b2=5,
∴(a﹣b)2=a2﹣2ab+b2,
=a2+b2﹣2ab
=5﹣2×(﹣2)
=9.
故答案为:9.
13.解:当(x﹣1)x+1=1时,x=﹣1时也成立,故①错误;
(x﹣1)(x2+ax+1)=x3+ax2+x﹣x2﹣ax﹣1
=x3+(a﹣1)x2+(1﹣a)x﹣1,
∵(x﹣1)(x2+ax+1)的运算结果中不含x2项,
∴a﹣1=0,
解得:a=1,故②错误;
∵a+b=10,ab=24,
∴(a﹣b)2=(a+b)2﹣4ab=102﹣4×24=4,
∴a﹣b=2或a﹣b=﹣2,故③正确;
∵4x=a,8y=b,
∴22x=a,23y=b,
∴22x﹣3y==,故④正确;
故答案为:③④.
14.解:由图2可知,
,
解得:,
则小长方形的面积为xy=3.
故答案为:3.
15.解:由图可知,
五边形ABGFD的面积=正方形ABCD的面积+梯形DCGF的面积,
=a2+(a+b)b
=,
阴影部分的面积=五边形ABGFD的面积﹣三角形ABD﹣三角形BCF
=﹣﹣
=
=,
∵a+b=10,ab=20,
∴a2+b2=(a+b)2﹣2ab=102﹣2×20=60,
∴阴影部分的面积为=30.
故答案为:30.
三.解答题
16.解:(1)原式=0.259×220×518×49=(0.25×4)9×(2×5)18×22=1×1018×4=4×1018;
(2)原式=20012﹣2×2001×1+1=(2001﹣1)2=20002=4000000=4×106.
17.解:(1)方法1,两个正方形的面积和,即a2+b2,
方法2,大正方形的面积减去两个长方形的面积,即(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)根据方法1与方法2所表示的面积相等得,a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)∵xy=3,
∴xy=6,
又∵(x+y)2=25,
∴x2+y2=(x+y)2﹣2xy=25﹣12=13.
18.解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴(x+y)2=36,(x﹣y)2=4,
又∵x>y>0,
∴x+y=6,x﹣y=2,
故答案为:2,6;
(2)大正方形的边长为x+y=9﹣m+m﹣4=5,
∵(9﹣m)(m﹣4)=4,
∴(9﹣m)2+(m﹣4)2=[(9﹣m)+(m﹣4)]2﹣2(9﹣m)(m﹣4)=52﹣8=17,
故答案为:5,17;
(3)a,b,c三边的数量关系为a2+b2=c2.理由如下:
由拼图可得,小正方形的边长为a﹣b,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
(a﹣b)2+ab×4=c2,
即a2+b2=c2.
一.选择题
1.下列代数式不是完全平方式的是( )
A.112mn+49m2+64n2 B.4m2+20mn+25n2
C.m2n2+2mn+4 D.m2+16m+64
2.下列等式一定成立的是( )
A.a2+a2=a5 B.(a+b)2=a2+b2
C.(2ab2)3=6a3b4 D.(x﹣a)(x﹣a)=x2﹣2ax+a2
3.如果x2+6xy+m是一个完全平方式,则m的值为( )
A.9y2 B.3y2 C.y2 D.6y2
4.若x2+y2=(x+y)2+A=(x﹣y)2﹣B,则A、B的数量关系为( )
A.相等 B.互为相反数 C.互为倒数 D.无法确定
5.计算(x﹣2)(2x+3)﹣(3x+1)2的结果中,x项的系数为( )
A.5 B.﹣5 C.7 D.﹣7
6.若25x2+kxy+4y2是完全平方公式,则k的值为( )
A.10或﹣20 B.﹣20 或20 C.5或﹣5 D.10或﹣10
7.若x2+2(m﹣5)x+16是完全平方式,则m的值是( )
A.5 B.9 C.9或1 D.5或1
8.小淇将(2019x+2020)2展开后得到a1x2+b1x+c1;小尧将(2020x﹣2019)2展开后得到a2x2+b2x+c2,若两人计算过程无误,则a1﹣a2的值为( )
A.﹣1 B.﹣4039 C.4039 D.1
9.若长方形的周长为36,其中一边长为x(x>0),面积为y,则y与x之间的关系为( )
A.y=(18﹣x)x B.y=x2 C.y=(36﹣x)x D.y=(18﹣x)2
10.如图,在边长为a+b的正方形的四个角上,分别剪去直角边长分别为a,b的四个直角三角形,则剩余部分面积,即图中的阴影部分的面积是( )
A.a2﹣b2 B.2ab C.a2+b2 D.4ab
二.填空题
11.代数式4x2+2(m﹣1)x+9是完全平方式,则m= .
12.若ab=﹣2,a2+b2=5,则(a﹣b)2的值为 .
13.以下四个结论正确的是 .(填序号)
①若(x﹣1)x+1=1,则x只能是2
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,则a=﹣1
③若a+b=10,ab=24,则a﹣b=2或a﹣b=﹣2
④若4x=a,8y=b,则22x﹣3y可表示为
14.如图1中的小长方形的长为x,宽为y,将四个同样的小长方形拼成如图2所示的正方形,则小长方形的面积为 .
15.如图所示,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么阴影部分的面积是 .
三.解答题
16.用简便方法计算(结果用科学记数法表示):
(1)0.259×220×259×643;
(2)20012﹣4002+1.
17.请认真观察图形,解答下列问题:
(1)根据图中条件,试用两种不同方法表示阴影部分的面积.方法1: ;方法2: .
(2)从中你能发现什么结论?请用乘法公式表示该结论: .
(3)运用你所得到的结论,解决问题:已知(x+y)2=25,xy=3,求x2+y2的值.
18.如图1,用4个相同边长是x,y的长方形和中间一个小正方形密铺而形成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则x﹣y值为 ;则x+y的值为 ;
(2)若小长方形两边长为9﹣m和m﹣4,则大正方形的边长为 ;若满足(9﹣m)(m﹣4)=4,则(9﹣m)2+(m﹣4)2的值为 ;
(3)如图2,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,猜想a,b,c三边的数量关系,并说明理由.
参考答案
一.选择题
1.解:A、原式=(7m+8n)2,故本选项不符合题意.
B、原式=(2m+5n)2,故本选项不符合题意.
C、该代数式不是完全平方式,故本选项符合题意.
D、原式=(m+8)2,故本选项不符合题意.
故选:C.
2.解:A、原式=2a2,所以A选项错误;
B、原式=a2+2ab+b2,所以B选项错误;
C、原式=8a2b6,所以C选项错误;
D、原式=(x﹣a)2=x2﹣2ax+a2,所以D选项正确.
故选:D.
3.解:∵x2+6xy+m是一个完全平方式,
∴m==9y2.
故选:A.
4.解:∵x2+y2=(x+y)2+(﹣2xy)=(x﹣y)2﹣(﹣2xy),
∴A=﹣2xy,B=﹣2xy,
∴A=B.
故选:A.
5.解:(x﹣2)(2x+3)﹣(3x+1)2
=2x2+3x﹣4x﹣6﹣9x2﹣6x﹣1
=﹣7x2﹣7x﹣7,
故选:D.
6.解:∵25x2+kxy+4y2是完全平方公式,
∴k=±2×5×2=±20,
故选:B.
7.解:∵x2+2(m﹣5)x+16是完全平方式,
∴m﹣5=±4,
解得:m=9或1,
则m的值是9或1.
故选:C.
8.解:∵(2019x+2020)2展开后得到a1x2+b1x+c1;
∴a1=20192,
∵(2020x﹣2019)2展开后得到a2x2+b2x+c2,
∴a2=20202,
∴a1﹣a2=20192﹣20202=(2019+2020)(2019﹣2020)=﹣4039,
故选:B.
9.解:长方形的周长为36,其中一边长为x(x>0),则另一边长为
36÷2﹣x=18﹣x,
∴y=x(18﹣x)
故选:A.
10.解:由题意得,S阴影部分=S正方形﹣4S三角形=(a+b)2﹣ab×4=a2+2ab+b2﹣2ab═a2+b2,
故选:C.
二.填空题
11.解:∵(2x±3)2=4x2±12x+9,
∴2(m﹣1)=±12,
∴m﹣1=±6,
∴m=7或m=﹣5.
故答案为:7或﹣5.
12.解:∵ab=﹣2,a2+b2=5,
∴(a﹣b)2=a2﹣2ab+b2,
=a2+b2﹣2ab
=5﹣2×(﹣2)
=9.
故答案为:9.
13.解:当(x﹣1)x+1=1时,x=﹣1时也成立,故①错误;
(x﹣1)(x2+ax+1)=x3+ax2+x﹣x2﹣ax﹣1
=x3+(a﹣1)x2+(1﹣a)x﹣1,
∵(x﹣1)(x2+ax+1)的运算结果中不含x2项,
∴a﹣1=0,
解得:a=1,故②错误;
∵a+b=10,ab=24,
∴(a﹣b)2=(a+b)2﹣4ab=102﹣4×24=4,
∴a﹣b=2或a﹣b=﹣2,故③正确;
∵4x=a,8y=b,
∴22x=a,23y=b,
∴22x﹣3y==,故④正确;
故答案为:③④.
14.解:由图2可知,
,
解得:,
则小长方形的面积为xy=3.
故答案为:3.
15.解:由图可知,
五边形ABGFD的面积=正方形ABCD的面积+梯形DCGF的面积,
=a2+(a+b)b
=,
阴影部分的面积=五边形ABGFD的面积﹣三角形ABD﹣三角形BCF
=﹣﹣
=
=,
∵a+b=10,ab=20,
∴a2+b2=(a+b)2﹣2ab=102﹣2×20=60,
∴阴影部分的面积为=30.
故答案为:30.
三.解答题
16.解:(1)原式=0.259×220×518×49=(0.25×4)9×(2×5)18×22=1×1018×4=4×1018;
(2)原式=20012﹣2×2001×1+1=(2001﹣1)2=20002=4000000=4×106.
17.解:(1)方法1,两个正方形的面积和,即a2+b2,
方法2,大正方形的面积减去两个长方形的面积,即(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)根据方法1与方法2所表示的面积相等得,a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)∵xy=3,
∴xy=6,
又∵(x+y)2=25,
∴x2+y2=(x+y)2﹣2xy=25﹣12=13.
18.解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴(x+y)2=36,(x﹣y)2=4,
又∵x>y>0,
∴x+y=6,x﹣y=2,
故答案为:2,6;
(2)大正方形的边长为x+y=9﹣m+m﹣4=5,
∵(9﹣m)(m﹣4)=4,
∴(9﹣m)2+(m﹣4)2=[(9﹣m)+(m﹣4)]2﹣2(9﹣m)(m﹣4)=52﹣8=17,
故答案为:5,17;
(3)a,b,c三边的数量关系为a2+b2=c2.理由如下:
由拼图可得,小正方形的边长为a﹣b,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
(a﹣b)2+ab×4=c2,
即a2+b2=c2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
