北师大版(2012)九年级下册数学随堂小练:2.4二次函数的应用(Word版有答案)
文档属性
| 名称 | 北师大版(2012)九年级下册数学随堂小练:2.4二次函数的应用(Word版有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 09:09:02 | ||
图片预览



文档简介
数学随堂小练北师大版(2012)九年级下册:2.4二次函数的应用
一、单选题
1.跳台滑雪是冬季奥运会比赛项目之一运动员起跳后的飞行路线可以看作是抛物线的一部分.运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关.如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为(
)
A.
B.
C.
D.
2.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是(
)
A.此抛物线的解析式是
B.篮圈中心的坐标是
C.此抛物线的顶点坐标是
D.篮球出手时离地面的高度是2m
3.某大学生利用课余时间在网上销售一种成本为50元/件的商品,每月的销售量y(件)与销售单价x(元)之间的函数关系式为,要获得最大利润,该商品的售价应定为(
)
A.60元
B.70元
C.80元
D.90元
4.某运动员在10m跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面(
)
A.10m
B.
C.
D.
5.矩形的周长为12cm,设其一边长为,面积为,则y与x的函数解析式及其自变量x的取值范围均正确的是(
)
A.
B.
C.
D.
6.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售价为x元,则可卖出件商品,那么卖出商品所赚钱y(元)与售价x(元)之间的函数关系式为(
)
A.
B.
C.
D.
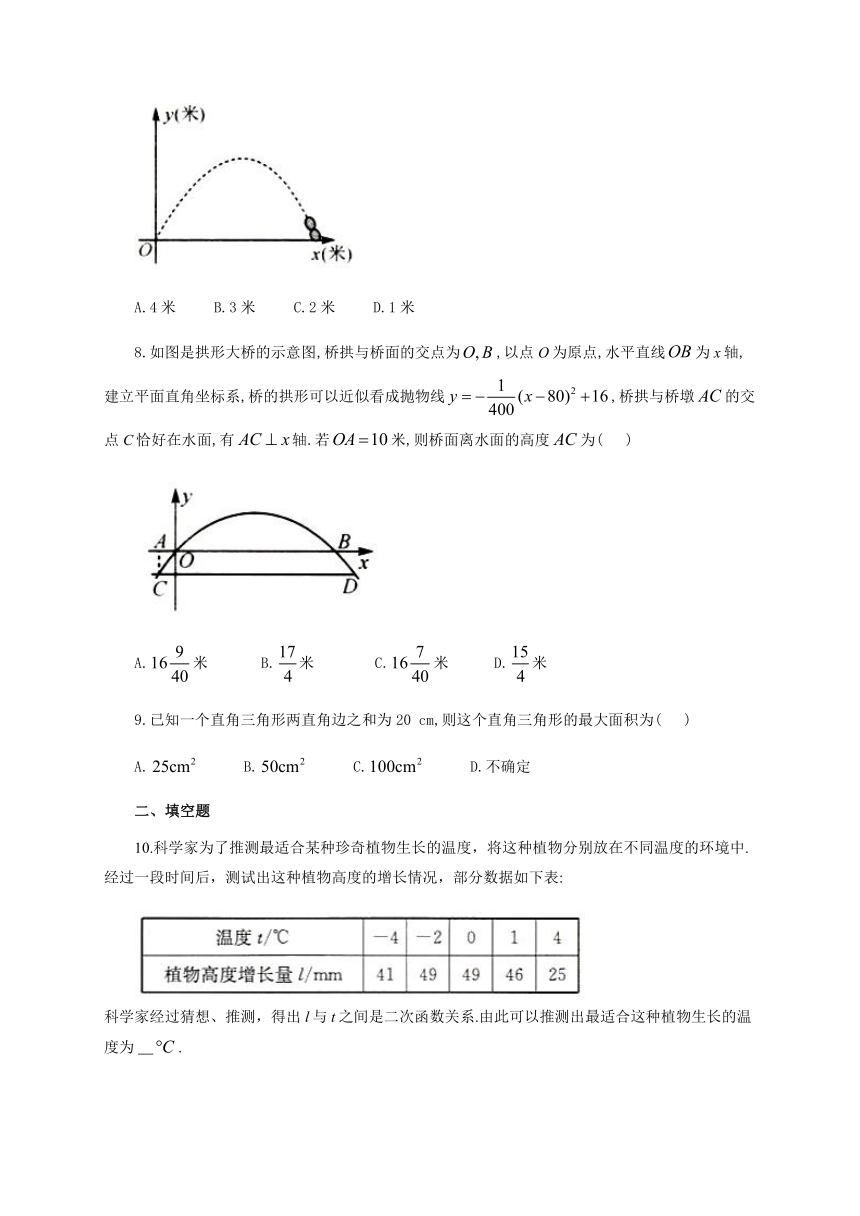
7.某广场有一喷水池.水从地面喷出.如图.以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是(
)
A.4米
B.3米
C.2米
D.1米
8.如图是拱形大桥的示意图,桥拱与桥面的交点为,以点O为原点,水平直线为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线,桥拱与桥墩的交点C恰好在水面,有轴.若米,则桥面离水面的高度为(
)
A.米
B.米
C.米
D.米
9.已知一个直角三角形两直角边之和为20
cm,则这个直角三角形的最大面积为(
)
A.
B.
C.
D.不确定
二、填空题
10.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中.经过一段时间后,测试出这种植物高度的增长情况,部分数据如下表:
科学家经过猜想、推测,得出l与t之间是二次函数关系.由此可以推测出最适合这种植物生长的温度为
.
11.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8
m,他在不弯腰的情况下,在棚内的横向活动范围是
m.
12.某花圃用花盆培育某种花苗,经过试验发现每盆的盈利数与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加2株(增加的株数为偶数),平均单株盈利就减少0.5元,则每盆植
株时能使单盆取得最大盈利;若需要单盆盈利不低于13元,则每盆需要植
株.
13.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(,且x为整数)出售,可卖出件,若使利润最大,则每件商品的售价应为
元.
三、解答题
14.科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程.
①在科研所到宿舍楼之间修一条高科技的道路;
②对宿舍楼进行防辐射处理,已知防辐射费y万元与科研所到宿舍楼的距离x
km之间的关系式为().当科研所到宿舍楼的距离为1
km时,防辐射费用为720万元;当科研所到宿舍楼的距离为3
km或大于3
km时,辐射影响忽略不计,不进行防辐射处理.
设修路的费用与成正比,且比例系数为m,配套工程费W=防辐射费+修路费.
(1)当科研所到宿舍楼的距离km时,防辐射费
万元,
,
.
(2)若,则当科研所到宿舍楼的距离为多少千米时,配套工程费最少?
(3)如果最低配套工程费不超过675万元,且科研所到宿舍楼的距离小于等于3
km,求m的范围.
参考答案
1.答案:B
根据题意知,抛物线经过点,
则
解得,
所以.
故选:B.
2.答案:A
抛物线的顶点坐标为,可设抛物线的函数关系式为.
篮圈中心的横坐标为,纵坐标为3.05,篮圈中心在抛物线上,
将它的坐标代入上式,得,,故A正确,B错误;
此抛物线的顶点坐标是,故C错误;当时,(m),
篮球出手时离地面2.25m,故D错误.
3.答案:C
设销售该商品每月所获总利润为W元,
则,
当时,W取得最大值,最大值为3600,
即售价为80元时,销售该商品所获利润最大,故选C
4.答案:D
抛物线的顶点坐标是,
运动员在空中运动的最大高度离水面
(m),故选D
5.答案:B
已知一边长为,则另一边长为cm.则化简得.故选B.
6.答案:B
每件商品售价为x元,则可卖出件商品,商品进价为每件21元.
商品所赚钱,
,
.
故选B.
7.答案:A
水在空中划出的曲线是抛物线的一部分,
水喷出的最大高度就是水在空中划出的抛物线的顶点的纵坐标,
,
顶点坐标为(2,4),
水喷出的最大高度为4米.
故选A.
8.答案:B
,
点A的横坐标为,
把代入中,得
,
则.
故选B.
9.答案:B
设直角三角形其中一条直角边为,则另一条直角边为.所以直角三角形的面积为,根据二次函数的性质可得函数图象开口向下,顶点坐标为(10,50),所以最大值为50,即三角形面积最大为.
故本题正确答案为B.
10.答案:
设l与t之间的关系式为,把分别代入得,解得,,即,
,当时,l取得最大值,为50,即当温度为时,最适合这种植物生长
11.答案:3
设抛物线的解析式为,由图得知点在抛物线上,列方程组得到抛物线的解析式为,根据题意求出时x的值,进而求出答案.
12.答案:7;7或9
根据已知假设每盆花苗(原来花盆中有3株)增加a(a为偶数)株,盈利为y元,则每盆花苗有株,得出平均单株盈利为元,由题意得,
根据二次函数的性质即可求得.
13.答案:25
设最大利润为w元,
则,
,
当时,二次函数有最大值25,
故答案为25.
14.答案:(1)0,-360,1080
(2)
①当时,配套工程费.
当时.;
②当时.,W随x增大而增大,
当时,.
当距离为2
km时,配套工程费最少.
(3),
,其对称轴,
当时,即,
,
,解得,
当时,即,
当时,,
解得:
故:
一、单选题
1.跳台滑雪是冬季奥运会比赛项目之一运动员起跳后的飞行路线可以看作是抛物线的一部分.运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关.如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为(
)
A.
B.
C.
D.
2.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是(
)
A.此抛物线的解析式是
B.篮圈中心的坐标是
C.此抛物线的顶点坐标是
D.篮球出手时离地面的高度是2m
3.某大学生利用课余时间在网上销售一种成本为50元/件的商品,每月的销售量y(件)与销售单价x(元)之间的函数关系式为,要获得最大利润,该商品的售价应定为(
)
A.60元
B.70元
C.80元
D.90元
4.某运动员在10m跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面(
)
A.10m
B.
C.
D.
5.矩形的周长为12cm,设其一边长为,面积为,则y与x的函数解析式及其自变量x的取值范围均正确的是(
)
A.
B.
C.
D.
6.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售价为x元,则可卖出件商品,那么卖出商品所赚钱y(元)与售价x(元)之间的函数关系式为(
)
A.
B.
C.
D.
7.某广场有一喷水池.水从地面喷出.如图.以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是(
)
A.4米
B.3米
C.2米
D.1米
8.如图是拱形大桥的示意图,桥拱与桥面的交点为,以点O为原点,水平直线为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线,桥拱与桥墩的交点C恰好在水面,有轴.若米,则桥面离水面的高度为(
)
A.米
B.米
C.米
D.米
9.已知一个直角三角形两直角边之和为20
cm,则这个直角三角形的最大面积为(
)
A.
B.
C.
D.不确定
二、填空题
10.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中.经过一段时间后,测试出这种植物高度的增长情况,部分数据如下表:
科学家经过猜想、推测,得出l与t之间是二次函数关系.由此可以推测出最适合这种植物生长的温度为
.
11.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8
m,他在不弯腰的情况下,在棚内的横向活动范围是
m.
12.某花圃用花盆培育某种花苗,经过试验发现每盆的盈利数与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加2株(增加的株数为偶数),平均单株盈利就减少0.5元,则每盆植
株时能使单盆取得最大盈利;若需要单盆盈利不低于13元,则每盆需要植
株.
13.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(,且x为整数)出售,可卖出件,若使利润最大,则每件商品的售价应为
元.
三、解答题
14.科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程.
①在科研所到宿舍楼之间修一条高科技的道路;
②对宿舍楼进行防辐射处理,已知防辐射费y万元与科研所到宿舍楼的距离x
km之间的关系式为().当科研所到宿舍楼的距离为1
km时,防辐射费用为720万元;当科研所到宿舍楼的距离为3
km或大于3
km时,辐射影响忽略不计,不进行防辐射处理.
设修路的费用与成正比,且比例系数为m,配套工程费W=防辐射费+修路费.
(1)当科研所到宿舍楼的距离km时,防辐射费
万元,
,
.
(2)若,则当科研所到宿舍楼的距离为多少千米时,配套工程费最少?
(3)如果最低配套工程费不超过675万元,且科研所到宿舍楼的距离小于等于3
km,求m的范围.
参考答案
1.答案:B
根据题意知,抛物线经过点,
则
解得,
所以.
故选:B.
2.答案:A
抛物线的顶点坐标为,可设抛物线的函数关系式为.
篮圈中心的横坐标为,纵坐标为3.05,篮圈中心在抛物线上,
将它的坐标代入上式,得,,故A正确,B错误;
此抛物线的顶点坐标是,故C错误;当时,(m),
篮球出手时离地面2.25m,故D错误.
3.答案:C
设销售该商品每月所获总利润为W元,
则,
当时,W取得最大值,最大值为3600,
即售价为80元时,销售该商品所获利润最大,故选C
4.答案:D
抛物线的顶点坐标是,
运动员在空中运动的最大高度离水面
(m),故选D
5.答案:B
已知一边长为,则另一边长为cm.则化简得.故选B.
6.答案:B
每件商品售价为x元,则可卖出件商品,商品进价为每件21元.
商品所赚钱,
,
.
故选B.
7.答案:A
水在空中划出的曲线是抛物线的一部分,
水喷出的最大高度就是水在空中划出的抛物线的顶点的纵坐标,
,
顶点坐标为(2,4),
水喷出的最大高度为4米.
故选A.
8.答案:B
,
点A的横坐标为,
把代入中,得
,
则.
故选B.
9.答案:B
设直角三角形其中一条直角边为,则另一条直角边为.所以直角三角形的面积为,根据二次函数的性质可得函数图象开口向下,顶点坐标为(10,50),所以最大值为50,即三角形面积最大为.
故本题正确答案为B.
10.答案:
设l与t之间的关系式为,把分别代入得,解得,,即,
,当时,l取得最大值,为50,即当温度为时,最适合这种植物生长
11.答案:3
设抛物线的解析式为,由图得知点在抛物线上,列方程组得到抛物线的解析式为,根据题意求出时x的值,进而求出答案.
12.答案:7;7或9
根据已知假设每盆花苗(原来花盆中有3株)增加a(a为偶数)株,盈利为y元,则每盆花苗有株,得出平均单株盈利为元,由题意得,
根据二次函数的性质即可求得.
13.答案:25
设最大利润为w元,
则,
,
当时,二次函数有最大值25,
故答案为25.
14.答案:(1)0,-360,1080
(2)
①当时,配套工程费.
当时.;
②当时.,W随x增大而增大,
当时,.
当距离为2
km时,配套工程费最少.
(3),
,其对称轴,
当时,即,
,
,解得,
当时,即,
当时,,
解得:
故:
