2020-2021学年上海市宝山区九年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市宝山区九年级上学期期中数学试卷 (Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 00:00:00 | ||
图片预览




文档简介
2020-2021学年上海市宝山区九年级第一学期期中数学试卷
一、选择题(共6小题).
1.(4分)如果4x﹣5y=0,那么的值是( )
A. B. C. D.4
2.(4分)如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A. B. C. D.
3.(4分)在直角坐标平面内有一点P(2,3),OP与x轴正半轴的夹角α的正弦值为( )
A. B. C. D.
4.(4分)已知线段a、b、c,求作线段x,使x=,则下列作法中(其中EF∥MN),正确的示意图是( )
A. B.
C. D.
5.(4分)已知是一个单位向量,、是非零向量,那么下列等式正确的是( )
A.||= B.||= C.= D.=
6.(4分)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
二、填空题(共12小题).
7.(4分)已知线段a=2厘米,c=8厘米,那么线段a和线段c的比例中项b= 厘米.
8.(4分)在比例尺为1:10000的地图上,如果点A与点B两点间的距离为5厘米,那么点A、B分别表示的两地间相距 米.
9.(4分)已知点M是线段AB的黄金分割点,线段AB的长度为12cm,那么较长的线段AM的长是 cm.
10.(4分)如图,△ABC中,点D在BC边上,如果要判定△ACD∽△BCA,那么需要增加的一个条件可以是 .
11.(4分)已知向量关系式3+4()=,那么用向量、表示向量= .
12.(4分)已知α是锐角,且sin(α+15°)=,那么tanα= .
13.(4分)如图,已知直线l1∥l2∥l3,如果DE:EF=2:3,AC=15,那么BC= .
14.(4分)如图,把一张矩形纸片沿着一条对称轴翻折,所得到的矩形ABCD与原矩形相似,已知原矩形纸片较短的边长为a,那么其较长边用含a的代数式表示为 .
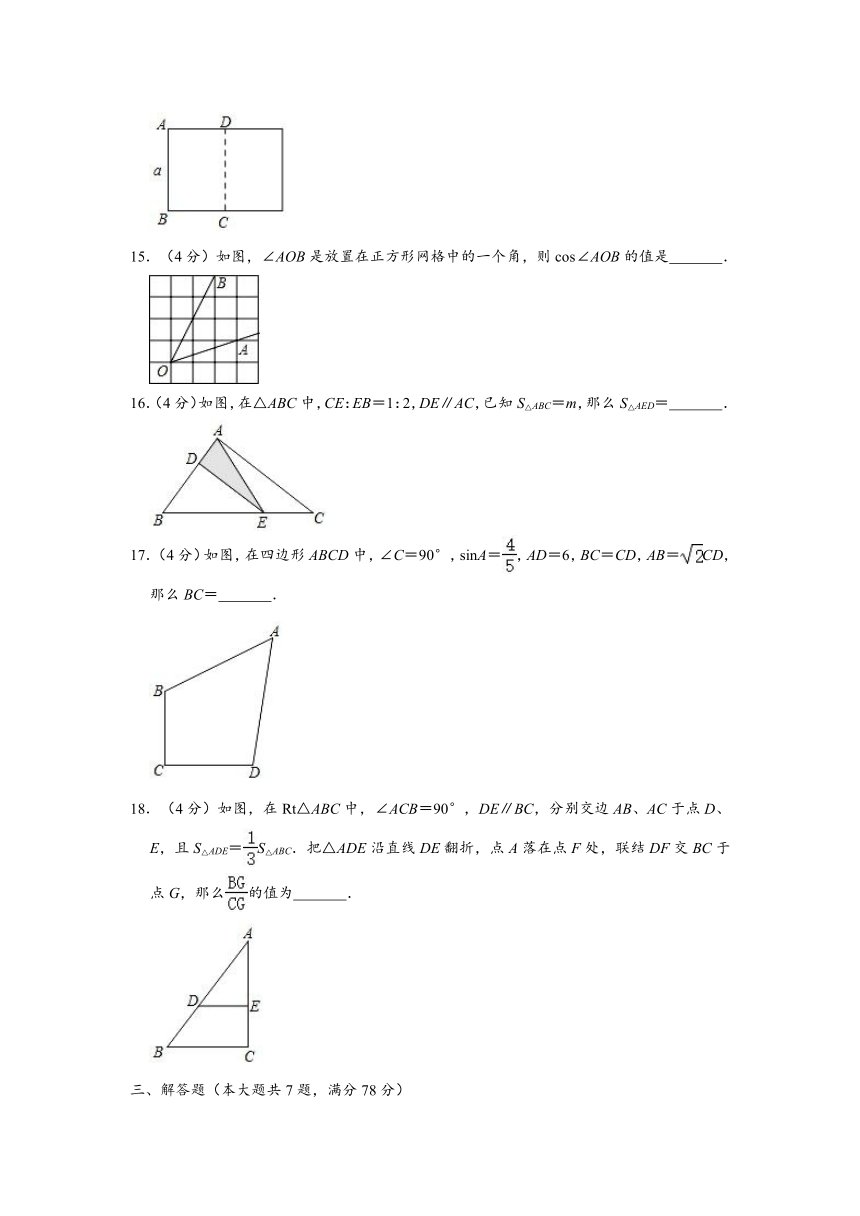
15.(4分)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
16.(4分)如图,在△ABC中,CE:EB=1:2,DE∥AC,已知S△ABC=m,那么S△AED= .
17.(4分)如图,在四边形ABCD中,∠C=90°,sinA=,AD=6,BC=CD,AB=CD,那么BC= .
18.(4分)如图,在Rt△ABC中,∠ACB=90°,DE∥BC,分别交边AB、AC于点D、E,且S△ADE=S△ABC.把△ADE沿直线DE翻折,点A落在点F处,联结DF交BC于点G,那么的值为 .
三、解答题(本大题共7题,满分78分)
19.(10分)求的值.
20.(10分)如图,已知向量、,先化简,再求作向量2+(﹣).(不要求写作法,但要指出图中表示结论的向量)
21.(10分)如图,已知点D、E分别在△ABC的边AB、AC上.
(1)如果=,且AD+DE+AE=15,求△ABC的周长;
(2)如果DE∥BC,过点D作DF∥AC,交BC于点F,且AE=7,CE=3,BF=,求FC的值.
22.(10分)如图,已知△ABC中,AD⊥BC,tanB=2,∠C=45°,AB=,点G是△ABC的重心,AG延长线交BC于点E.
(1)求BC的长;
(2)求证:DG∥AB.
23.(12分)如图,已知点M是平行四边形ABCD的对角线BD上的一点,射线AM与BC交于点F,与DC延长线交于点H.
(1)求证:AM2=MF?MH;
(2)如果CF:FB=1:2,求的值.
24.(12分)如图,在正方形ABCD中,点E、F分别在边AD、AB上,AE=ED,AF=BF.
(1)求证:△AEF∽△BFC;
(2)求cos∠ECF的值;
(3)联结BD,交CF于点M,交CE于点N,求的值.
25.(14分)如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD=3,BC=6,CD=4.点M是边BC上一个动点(不与点B重合),在边AB上取点E,连接DM、ME.
(1)若点M是BC的中点,且∠EMD=90°,求tan∠EDM的值;
(2)若∠EMD=∠B,设CM=x,BE=y,求y关于x的函数关系式;
(3)在(2)条件下,当△DME为等腰三角形时,求CM的长.
参考答案
一、选择题(共6小题).
1.(4分)如果4x﹣5y=0,那么的值是( )
A. B. C. D.4
解:∵4x﹣5y=0,
∴=,
∴=﹣1=﹣1=;
故选:C.
2.(4分)如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A. B. C. D.
解:A、∵,不能判定DE∥AC,选项符合题意;
B、∵,∴DE∥AC,选项不符合题意;
C、∵,∴,∴DE∥AC,选项不符合题意;
D、∵,∴,∴DE∥AC,选项不符合题意;
故选:A.
3.(4分)在直角坐标平面内有一点P(2,3),OP与x轴正半轴的夹角α的正弦值为( )
A. B. C. D.
解:如图,作PE⊥x轴于E.
∵P(2,3),
∴OE=2,PE=3,
∴OP===,
∴sinα===,
故选:D.
4.(4分)已知线段a、b、c,求作线段x,使x=,则下列作法中(其中EF∥MN),正确的示意图是( )
A. B.
C. D.
解:∵已知线段a、b、c,x=,
可得:,
故选:D.
5.(4分)已知是一个单位向量,、是非零向量,那么下列等式正确的是( )
A.||= B.||= C.= D.=
解:A、由于单位向量只限制长度,不确定方向,故本选项错误;
B、符合向量的长度及方向,故本选项正确;
C、得出的是a的方向不是单位向量,故本选项错误;
D、左边得出的是a的方向,右边得出的是b的方向,两者方向不一定相同,故本选项错误.
故选:B.
6.(4分)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
解:A、相似:∵∠A=55°∴∠B=90°﹣55°=35°∵∠D=35°∴∠B=∠D∵∠C=∠F∴△ABC∽△DEF;
B、相似:∵AC=9,BC=12,DF=6,EF=8,∴,∵∠C=∠F∴△ABC∽△DEF;
C、有一组角相等两边对应成比例,但该组角不是这两边的夹角,故不相似;
D、相似:由题意AB=10,AC=8,可得BC=6,∵DE=15,EF=9,∴,∵∠B=∠E,∴△ABC∽△DEF;
故选:C.
二、填空题(本大题共12题,每题4分,满分48分)
7.(4分)已知线段a=2厘米,c=8厘米,那么线段a和线段c的比例中项b= 4 厘米.
解:∵线段b是a、c的比例中项,
∴b2=ac=16,
解得:b=±4,
又∵线段是正数,
∴b=4(厘米).
故答案为:4.
8.(4分)在比例尺为1:10000的地图上,如果点A与点B两点间的距离为5厘米,那么点A、B分别表示的两地间相距 500 米.
解:设两地间的实际距离是x厘米,
∵比例尺为1:10000,量得两地间的距离为5厘米,
∴,
解得:x=50000,
∵50000厘米=500米,
∴两地间的实际距离是500米.
故答案为:500.
9.(4分)已知点M是线段AB的黄金分割点,线段AB的长度为12cm,那么较长的线段AM的长是 (6﹣6) cm.
解:∵点M是线段AB的黄金分割点,AM>BM,
∴AM=AB=(6﹣6)厘米,
故答案为:(6﹣6).
10.(4分)如图,△ABC中,点D在BC边上,如果要判定△ACD∽△BCA,那么需要增加的一个条件可以是 ∠DAC=∠ABC或∠ADC=∠BAC或 .
解:∵从图中可知∠C为公共角,
∴如果再加上∠DAC=∠ABC或∠ADC=∠BAC或都可判定△ADE∽△ABC,
故答案为:∠DAC=∠ABC或∠ADC=∠BAC或.
11.(4分)已知向量关系式3+4()=,那么用向量、表示向量= + .
解:∵3+4()=,
∴=+,
故答案为:+.
12.(4分)已知α是锐角,且sin(α+15°)=,那么tanα= 1 .
解:∵sin60°=,
∴α+15°=60°,
解得,α=45°,
∴tanα=tan45°=1,
故答案为:1.
13.(4分)如图,已知直线l1∥l2∥l3,如果DE:EF=2:3,AC=15,那么BC= 9 .
解:∵l1∥l2∥l3,
∴,
∴,
∵AC=15,
∴BC=9,
故答案为:9.
14.(4分)如图,把一张矩形纸片沿着一条对称轴翻折,所得到的矩形ABCD与原矩形相似,已知原矩形纸片较短的边长为a,那么其较长边用含a的代数式表示为 a .
解:设较长边为b,
∵所得到的矩形ABCD与原矩形相似,
∴=,
整理得,b2=2a2,
解得,b=a,
故答案为:a.
15.(4分)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
解:连接AB,
∵OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,
∴OA2+AB2=OB2,OA=AB,
∴△AOB是等腰直角三角形,即∠OAB=90°,
∴∠AOB=45°,
∴cos∠AOB=cos45°=.
故答案为:.
16.(4分)如图,在△ABC中,CE:EB=1:2,DE∥AC,已知S△ABC=m,那么S△AED= m .
解:∵CE:EB=1:2,设CE=k,则EB=2k,
∵DE∥AC,
∴BE:BC=2k:3k=2:3,
∴=()2,
∴S△BDE=m,
∵DE∥AC,
∴==,
∴==,
则S△ADE=S△BDE=m.
故答案为m.
17.(4分)如图,在四边形ABCD中,∠C=90°,sinA=,AD=6,BC=CD,AB=CD,那么BC= .
解:作BE⊥AD于E,连接BD,如图所示:
设BC=CD=x,则AB=x,
∵sinA==,
∴BE=AB=x,
∴AE===x,
∵BC=CD,∠C=90°,
∴BD=BC=x,
∴BD=AB,
∵BE⊥AD,
∴AE=DE=AD=3,
∴x=3,
解得:x=,
即BC=,
故答案为:.
18.(4分)如图,在Rt△ABC中,∠ACB=90°,DE∥BC,分别交边AB、AC于点D、E,且S△ADE=S△ABC.把△ADE沿直线DE翻折,点A落在点F处,联结DF交BC于点G,那么的值为 2+2 .
解:如图,
∵DE∥BC,
∴△ADE∽△ABC,
∴=()2,
∵S△ADE=S△ABC,
∴,
∴AE=AC,
∴EC=AC﹣AE=AC,
∵△ADE∽△ABC,
∴,
∴DE=BC,
∵把△ADE沿直线DE翻折,
∴AE=EF=AC,
∴CF=EF﹣EC=AC,
∵GC∥DE,
∴△GCF∽△DEF,
∴,
∴=2﹣,
∴GC=BC,
∴BG=BC﹣GC=BC,
∴=2+2,
故答案为:2+2.
三、解答题(本大题共7题,满分78分)
19.(10分)求的值.
解:原式=
=
=2﹣.
20.(10分)如图,已知向量、,先化简,再求作向量2+(﹣).(不要求写作法,但要指出图中表示结论的向量)
解:2+(﹣)
=2+﹣
=+.
如图,即为所求.
21.(10分)如图,已知点D、E分别在△ABC的边AB、AC上.
(1)如果=,且AD+DE+AE=15,求△ABC的周长;
(2)如果DE∥BC,过点D作DF∥AC,交BC于点F,且AE=7,CE=3,BF=,求FC的值.
解:(1)∵=,∠A=∠A,
∴△ADE∽△ABC,
∴,
∴,
∵AD+DE+AE=15,
∴AB+AC+BC=25,
∴△ABC的周长为25;
(2)如图,
∵DE∥BC,DF∥AC,
∴四边形DECF是平行四边形,
∴DF=EC=3,
∵DF∥AC,
∴△DFB∽△ACB,
∴,
∴=,
∴BC=6,
∴FC=BC﹣BF=6﹣=.
22.(10分)如图,已知△ABC中,AD⊥BC,tanB=2,∠C=45°,AB=,点G是△ABC的重心,AG延长线交BC于点E.
(1)求BC的长;
(2)求证:DG∥AB.
【解答】(1)解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∵tanB==2,
∴AD=2BD,
∵BD2+AD2=AB2,
∴BD2+4BD2=()2,解得BD=1,
∴AD=2,
在Rt△ADC中,∵∠C=45°,
∴CD=AD=2,
∴BC=BD+CD=1+2=3;
(2)解:∵点G是△ABC的重心,
∴AG=2GE,BE=CE=BC=,
∴DE=BE﹣BD=﹣1=,
∵=,==,
∴=,
而∠DEG=∠BEA,
∴△EDG∽△EBA,
∴∠EDG=∠B,
∴DG∥AB.
23.(12分)如图,已知点M是平行四边形ABCD的对角线BD上的一点,射线AM与BC交于点F,与DC延长线交于点H.
(1)求证:AM2=MF?MH;
(2)如果CF:FB=1:2,求的值.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥AD,
∴△ABM∽△HDM,△BFM∽△DAM,
∴,,
∴,
∴AM2=MF?MH;
(2)∵CF:FB=1:2,
∴=,
∵四边形ABCD是平行四边形,
∴AB∥CD,∠ADC=∠ABC,
∴∠H=∠BAF,
∴△BAF∽△DHA,
∴=()2=.
24.(12分)如图,在正方形ABCD中,点E、F分别在边AD、AB上,AE=ED,AF=BF.
(1)求证:△AEF∽△BFC;
(2)求cos∠ECF的值;
(3)联结BD,交CF于点M,交CE于点N,求的值.
【解答】(1)证明:设正方形的边长为4a,
∵四边形ABCD为正方形,
设正方形的边长为4a,
∴∠A=∠ABC=90°,
AD=AB=BC=4a,
∵AE=ED=a,AF=BF=2a,
∴==,==,
∴=,
而∠A=∠FBC,
∴△AEF∽△BFC;
(2)解:在Rt△AEF中,EF==a,
在Rt△BCF中,CF==2a,
在Rt△DEC中,CE==5a,
∵EF2+CF2=CE2,
∴△CEF为直角三角形,∠EFC=90°,
∴cos∠ECF===;
(3)解:∵BF∥CD,
∴△BMF∽△DMC,
∴===,
即BM=DM,
∴BM=BD,
∵DE∥BC,
∴△DEN∽△BCN,
∴===,
∴DN=BN=BD,
∴MN=BD﹣BM﹣DN=BD﹣BD﹣BD=BD,
∴=.
25.(14分)如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD=3,BC=6,CD=4.点M是边BC上一个动点(不与点B重合),在边AB上取点E,连接DM、ME.
(1)若点M是BC的中点,且∠EMD=90°,求tan∠EDM的值;
(2)若∠EMD=∠B,设CM=x,BE=y,求y关于x的函数关系式;
(3)在(2)条件下,当△DME为等腰三角形时,求CM的长.
解:(1)如图1,
∵点M是BC的中点,BC=6,
∴BM=CM=3,
∴MD===5,
∵AD=BM=3,AD∥BC,
∴四边形ABMD是平行四边形,
∴S平行四边形ABMD=BM×CD=MD×EM,
∴3×4=5EM,
∴EM=,
∴tan∠EDM===;
(2)如图2,过点M作MN⊥AB于N,
∵CM=x,BC=6,
∴BM=6﹣x,
由(1)可知sinB==,
∴sinB==,cosB=,
∴MN=(6﹣x),BN=(6﹣x),
∵∠EMC=∠B+∠BEM=∠EMD+∠DMC,∠B=∠EMD,
∴∠BEM=∠DMC,
又∵∠C=∠ENM,
∴△ENM∽△MCD,
∴,
∴=,
∴y=﹣+x+;
(3)当EM=DM时,
∵△ENM∽△MCD,
∴,
∴=1,
∴x=1,
∴CM=1,
当EM=DE时,如图3,过点E作EH⊥DM,
∴MH=DH,
∵cosB=cos∠DME=,
∴=,
∵△ENM∽△MCD,
∴,
∴=,
∴x=,
∴CM=;
当DE=DM时,如图4,过点D作DH⊥EM于H,
∴EH=HM,
∵cosB=cos∠DME==,
∴==,
∵△ENM∽△MCD,
∴,
∴=,
∴x=0(不合题意),
综上所述:CM=1或.
一、选择题(共6小题).
1.(4分)如果4x﹣5y=0,那么的值是( )
A. B. C. D.4
2.(4分)如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A. B. C. D.
3.(4分)在直角坐标平面内有一点P(2,3),OP与x轴正半轴的夹角α的正弦值为( )
A. B. C. D.
4.(4分)已知线段a、b、c,求作线段x,使x=,则下列作法中(其中EF∥MN),正确的示意图是( )
A. B.
C. D.
5.(4分)已知是一个单位向量,、是非零向量,那么下列等式正确的是( )
A.||= B.||= C.= D.=
6.(4分)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
二、填空题(共12小题).
7.(4分)已知线段a=2厘米,c=8厘米,那么线段a和线段c的比例中项b= 厘米.
8.(4分)在比例尺为1:10000的地图上,如果点A与点B两点间的距离为5厘米,那么点A、B分别表示的两地间相距 米.
9.(4分)已知点M是线段AB的黄金分割点,线段AB的长度为12cm,那么较长的线段AM的长是 cm.
10.(4分)如图,△ABC中,点D在BC边上,如果要判定△ACD∽△BCA,那么需要增加的一个条件可以是 .
11.(4分)已知向量关系式3+4()=,那么用向量、表示向量= .
12.(4分)已知α是锐角,且sin(α+15°)=,那么tanα= .
13.(4分)如图,已知直线l1∥l2∥l3,如果DE:EF=2:3,AC=15,那么BC= .
14.(4分)如图,把一张矩形纸片沿着一条对称轴翻折,所得到的矩形ABCD与原矩形相似,已知原矩形纸片较短的边长为a,那么其较长边用含a的代数式表示为 .
15.(4分)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
16.(4分)如图,在△ABC中,CE:EB=1:2,DE∥AC,已知S△ABC=m,那么S△AED= .
17.(4分)如图,在四边形ABCD中,∠C=90°,sinA=,AD=6,BC=CD,AB=CD,那么BC= .
18.(4分)如图,在Rt△ABC中,∠ACB=90°,DE∥BC,分别交边AB、AC于点D、E,且S△ADE=S△ABC.把△ADE沿直线DE翻折,点A落在点F处,联结DF交BC于点G,那么的值为 .
三、解答题(本大题共7题,满分78分)
19.(10分)求的值.
20.(10分)如图,已知向量、,先化简,再求作向量2+(﹣).(不要求写作法,但要指出图中表示结论的向量)
21.(10分)如图,已知点D、E分别在△ABC的边AB、AC上.
(1)如果=,且AD+DE+AE=15,求△ABC的周长;
(2)如果DE∥BC,过点D作DF∥AC,交BC于点F,且AE=7,CE=3,BF=,求FC的值.
22.(10分)如图,已知△ABC中,AD⊥BC,tanB=2,∠C=45°,AB=,点G是△ABC的重心,AG延长线交BC于点E.
(1)求BC的长;
(2)求证:DG∥AB.
23.(12分)如图,已知点M是平行四边形ABCD的对角线BD上的一点,射线AM与BC交于点F,与DC延长线交于点H.
(1)求证:AM2=MF?MH;
(2)如果CF:FB=1:2,求的值.
24.(12分)如图,在正方形ABCD中,点E、F分别在边AD、AB上,AE=ED,AF=BF.
(1)求证:△AEF∽△BFC;
(2)求cos∠ECF的值;
(3)联结BD,交CF于点M,交CE于点N,求的值.
25.(14分)如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD=3,BC=6,CD=4.点M是边BC上一个动点(不与点B重合),在边AB上取点E,连接DM、ME.
(1)若点M是BC的中点,且∠EMD=90°,求tan∠EDM的值;
(2)若∠EMD=∠B,设CM=x,BE=y,求y关于x的函数关系式;
(3)在(2)条件下,当△DME为等腰三角形时,求CM的长.
参考答案
一、选择题(共6小题).
1.(4分)如果4x﹣5y=0,那么的值是( )
A. B. C. D.4
解:∵4x﹣5y=0,
∴=,
∴=﹣1=﹣1=;
故选:C.
2.(4分)如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A. B. C. D.
解:A、∵,不能判定DE∥AC,选项符合题意;
B、∵,∴DE∥AC,选项不符合题意;
C、∵,∴,∴DE∥AC,选项不符合题意;
D、∵,∴,∴DE∥AC,选项不符合题意;
故选:A.
3.(4分)在直角坐标平面内有一点P(2,3),OP与x轴正半轴的夹角α的正弦值为( )
A. B. C. D.
解:如图,作PE⊥x轴于E.
∵P(2,3),
∴OE=2,PE=3,
∴OP===,
∴sinα===,
故选:D.
4.(4分)已知线段a、b、c,求作线段x,使x=,则下列作法中(其中EF∥MN),正确的示意图是( )
A. B.
C. D.
解:∵已知线段a、b、c,x=,
可得:,
故选:D.
5.(4分)已知是一个单位向量,、是非零向量,那么下列等式正确的是( )
A.||= B.||= C.= D.=
解:A、由于单位向量只限制长度,不确定方向,故本选项错误;
B、符合向量的长度及方向,故本选项正确;
C、得出的是a的方向不是单位向量,故本选项错误;
D、左边得出的是a的方向,右边得出的是b的方向,两者方向不一定相同,故本选项错误.
故选:B.
6.(4分)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
解:A、相似:∵∠A=55°∴∠B=90°﹣55°=35°∵∠D=35°∴∠B=∠D∵∠C=∠F∴△ABC∽△DEF;
B、相似:∵AC=9,BC=12,DF=6,EF=8,∴,∵∠C=∠F∴△ABC∽△DEF;
C、有一组角相等两边对应成比例,但该组角不是这两边的夹角,故不相似;
D、相似:由题意AB=10,AC=8,可得BC=6,∵DE=15,EF=9,∴,∵∠B=∠E,∴△ABC∽△DEF;
故选:C.
二、填空题(本大题共12题,每题4分,满分48分)
7.(4分)已知线段a=2厘米,c=8厘米,那么线段a和线段c的比例中项b= 4 厘米.
解:∵线段b是a、c的比例中项,
∴b2=ac=16,
解得:b=±4,
又∵线段是正数,
∴b=4(厘米).
故答案为:4.
8.(4分)在比例尺为1:10000的地图上,如果点A与点B两点间的距离为5厘米,那么点A、B分别表示的两地间相距 500 米.
解:设两地间的实际距离是x厘米,
∵比例尺为1:10000,量得两地间的距离为5厘米,
∴,
解得:x=50000,
∵50000厘米=500米,
∴两地间的实际距离是500米.
故答案为:500.
9.(4分)已知点M是线段AB的黄金分割点,线段AB的长度为12cm,那么较长的线段AM的长是 (6﹣6) cm.
解:∵点M是线段AB的黄金分割点,AM>BM,
∴AM=AB=(6﹣6)厘米,
故答案为:(6﹣6).
10.(4分)如图,△ABC中,点D在BC边上,如果要判定△ACD∽△BCA,那么需要增加的一个条件可以是 ∠DAC=∠ABC或∠ADC=∠BAC或 .
解:∵从图中可知∠C为公共角,
∴如果再加上∠DAC=∠ABC或∠ADC=∠BAC或都可判定△ADE∽△ABC,
故答案为:∠DAC=∠ABC或∠ADC=∠BAC或.
11.(4分)已知向量关系式3+4()=,那么用向量、表示向量= + .
解:∵3+4()=,
∴=+,
故答案为:+.
12.(4分)已知α是锐角,且sin(α+15°)=,那么tanα= 1 .
解:∵sin60°=,
∴α+15°=60°,
解得,α=45°,
∴tanα=tan45°=1,
故答案为:1.
13.(4分)如图,已知直线l1∥l2∥l3,如果DE:EF=2:3,AC=15,那么BC= 9 .
解:∵l1∥l2∥l3,
∴,
∴,
∵AC=15,
∴BC=9,
故答案为:9.
14.(4分)如图,把一张矩形纸片沿着一条对称轴翻折,所得到的矩形ABCD与原矩形相似,已知原矩形纸片较短的边长为a,那么其较长边用含a的代数式表示为 a .
解:设较长边为b,
∵所得到的矩形ABCD与原矩形相似,
∴=,
整理得,b2=2a2,
解得,b=a,
故答案为:a.
15.(4分)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
解:连接AB,
∵OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,
∴OA2+AB2=OB2,OA=AB,
∴△AOB是等腰直角三角形,即∠OAB=90°,
∴∠AOB=45°,
∴cos∠AOB=cos45°=.
故答案为:.
16.(4分)如图,在△ABC中,CE:EB=1:2,DE∥AC,已知S△ABC=m,那么S△AED= m .
解:∵CE:EB=1:2,设CE=k,则EB=2k,
∵DE∥AC,
∴BE:BC=2k:3k=2:3,
∴=()2,
∴S△BDE=m,
∵DE∥AC,
∴==,
∴==,
则S△ADE=S△BDE=m.
故答案为m.
17.(4分)如图,在四边形ABCD中,∠C=90°,sinA=,AD=6,BC=CD,AB=CD,那么BC= .
解:作BE⊥AD于E,连接BD,如图所示:
设BC=CD=x,则AB=x,
∵sinA==,
∴BE=AB=x,
∴AE===x,
∵BC=CD,∠C=90°,
∴BD=BC=x,
∴BD=AB,
∵BE⊥AD,
∴AE=DE=AD=3,
∴x=3,
解得:x=,
即BC=,
故答案为:.
18.(4分)如图,在Rt△ABC中,∠ACB=90°,DE∥BC,分别交边AB、AC于点D、E,且S△ADE=S△ABC.把△ADE沿直线DE翻折,点A落在点F处,联结DF交BC于点G,那么的值为 2+2 .
解:如图,
∵DE∥BC,
∴△ADE∽△ABC,
∴=()2,
∵S△ADE=S△ABC,
∴,
∴AE=AC,
∴EC=AC﹣AE=AC,
∵△ADE∽△ABC,
∴,
∴DE=BC,
∵把△ADE沿直线DE翻折,
∴AE=EF=AC,
∴CF=EF﹣EC=AC,
∵GC∥DE,
∴△GCF∽△DEF,
∴,
∴=2﹣,
∴GC=BC,
∴BG=BC﹣GC=BC,
∴=2+2,
故答案为:2+2.
三、解答题(本大题共7题,满分78分)
19.(10分)求的值.
解:原式=
=
=2﹣.
20.(10分)如图,已知向量、,先化简,再求作向量2+(﹣).(不要求写作法,但要指出图中表示结论的向量)
解:2+(﹣)
=2+﹣
=+.
如图,即为所求.
21.(10分)如图,已知点D、E分别在△ABC的边AB、AC上.
(1)如果=,且AD+DE+AE=15,求△ABC的周长;
(2)如果DE∥BC,过点D作DF∥AC,交BC于点F,且AE=7,CE=3,BF=,求FC的值.
解:(1)∵=,∠A=∠A,
∴△ADE∽△ABC,
∴,
∴,
∵AD+DE+AE=15,
∴AB+AC+BC=25,
∴△ABC的周长为25;
(2)如图,
∵DE∥BC,DF∥AC,
∴四边形DECF是平行四边形,
∴DF=EC=3,
∵DF∥AC,
∴△DFB∽△ACB,
∴,
∴=,
∴BC=6,
∴FC=BC﹣BF=6﹣=.
22.(10分)如图,已知△ABC中,AD⊥BC,tanB=2,∠C=45°,AB=,点G是△ABC的重心,AG延长线交BC于点E.
(1)求BC的长;
(2)求证:DG∥AB.
【解答】(1)解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∵tanB==2,
∴AD=2BD,
∵BD2+AD2=AB2,
∴BD2+4BD2=()2,解得BD=1,
∴AD=2,
在Rt△ADC中,∵∠C=45°,
∴CD=AD=2,
∴BC=BD+CD=1+2=3;
(2)解:∵点G是△ABC的重心,
∴AG=2GE,BE=CE=BC=,
∴DE=BE﹣BD=﹣1=,
∵=,==,
∴=,
而∠DEG=∠BEA,
∴△EDG∽△EBA,
∴∠EDG=∠B,
∴DG∥AB.
23.(12分)如图,已知点M是平行四边形ABCD的对角线BD上的一点,射线AM与BC交于点F,与DC延长线交于点H.
(1)求证:AM2=MF?MH;
(2)如果CF:FB=1:2,求的值.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥AD,
∴△ABM∽△HDM,△BFM∽△DAM,
∴,,
∴,
∴AM2=MF?MH;
(2)∵CF:FB=1:2,
∴=,
∵四边形ABCD是平行四边形,
∴AB∥CD,∠ADC=∠ABC,
∴∠H=∠BAF,
∴△BAF∽△DHA,
∴=()2=.
24.(12分)如图,在正方形ABCD中,点E、F分别在边AD、AB上,AE=ED,AF=BF.
(1)求证:△AEF∽△BFC;
(2)求cos∠ECF的值;
(3)联结BD,交CF于点M,交CE于点N,求的值.
【解答】(1)证明:设正方形的边长为4a,
∵四边形ABCD为正方形,
设正方形的边长为4a,
∴∠A=∠ABC=90°,
AD=AB=BC=4a,
∵AE=ED=a,AF=BF=2a,
∴==,==,
∴=,
而∠A=∠FBC,
∴△AEF∽△BFC;
(2)解:在Rt△AEF中,EF==a,
在Rt△BCF中,CF==2a,
在Rt△DEC中,CE==5a,
∵EF2+CF2=CE2,
∴△CEF为直角三角形,∠EFC=90°,
∴cos∠ECF===;
(3)解:∵BF∥CD,
∴△BMF∽△DMC,
∴===,
即BM=DM,
∴BM=BD,
∵DE∥BC,
∴△DEN∽△BCN,
∴===,
∴DN=BN=BD,
∴MN=BD﹣BM﹣DN=BD﹣BD﹣BD=BD,
∴=.
25.(14分)如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD=3,BC=6,CD=4.点M是边BC上一个动点(不与点B重合),在边AB上取点E,连接DM、ME.
(1)若点M是BC的中点,且∠EMD=90°,求tan∠EDM的值;
(2)若∠EMD=∠B,设CM=x,BE=y,求y关于x的函数关系式;
(3)在(2)条件下,当△DME为等腰三角形时,求CM的长.
解:(1)如图1,
∵点M是BC的中点,BC=6,
∴BM=CM=3,
∴MD===5,
∵AD=BM=3,AD∥BC,
∴四边形ABMD是平行四边形,
∴S平行四边形ABMD=BM×CD=MD×EM,
∴3×4=5EM,
∴EM=,
∴tan∠EDM===;
(2)如图2,过点M作MN⊥AB于N,
∵CM=x,BC=6,
∴BM=6﹣x,
由(1)可知sinB==,
∴sinB==,cosB=,
∴MN=(6﹣x),BN=(6﹣x),
∵∠EMC=∠B+∠BEM=∠EMD+∠DMC,∠B=∠EMD,
∴∠BEM=∠DMC,
又∵∠C=∠ENM,
∴△ENM∽△MCD,
∴,
∴=,
∴y=﹣+x+;
(3)当EM=DM时,
∵△ENM∽△MCD,
∴,
∴=1,
∴x=1,
∴CM=1,
当EM=DE时,如图3,过点E作EH⊥DM,
∴MH=DH,
∵cosB=cos∠DME=,
∴=,
∵△ENM∽△MCD,
∴,
∴=,
∴x=,
∴CM=;
当DE=DM时,如图4,过点D作DH⊥EM于H,
∴EH=HM,
∵cosB=cos∠DME==,
∴==,
∵△ENM∽△MCD,
∴,
∴=,
∴x=0(不合题意),
综上所述:CM=1或.
同课章节目录
