人教版数学七年级上册1.3. 1有理数的加法课件(17张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.3. 1有理数的加法课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 15:17:03 | ||
图片预览

文档简介
1.3.1 有理数的加法法则
我是火炬手
演示1
+1
-1
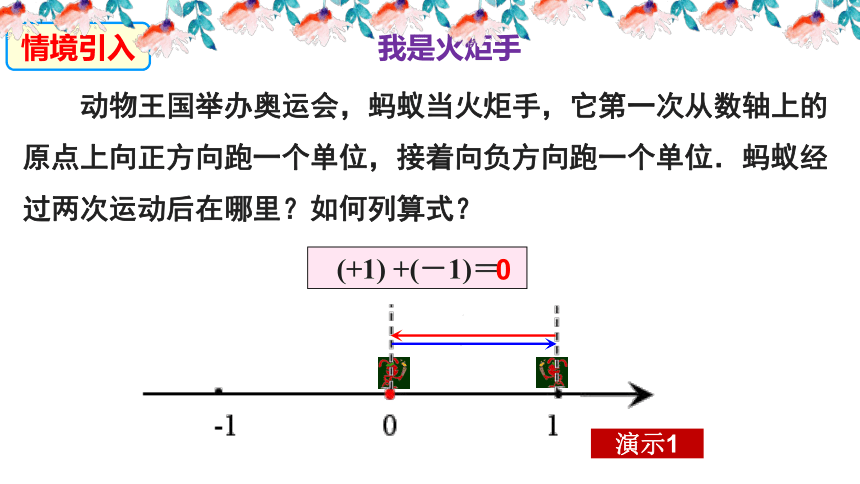
(+1) +(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
情境引入
合作探究
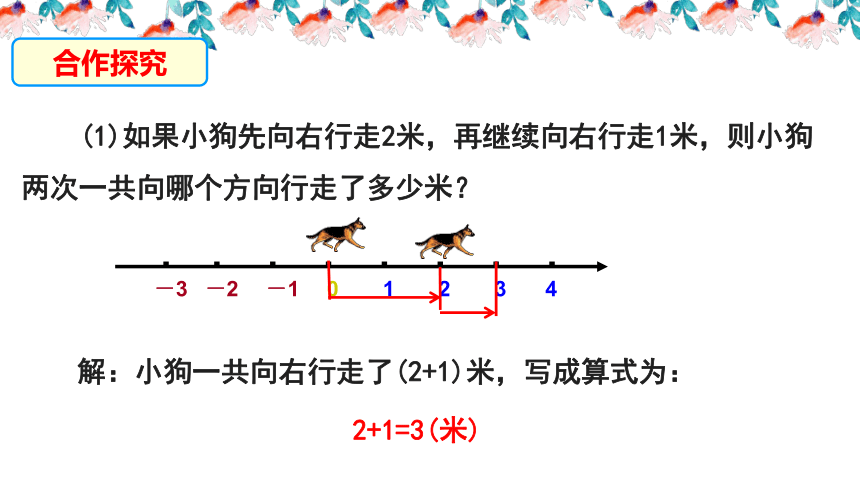
(1)如果小狗先向右行走2米,再继续向右行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
解:小狗一共向右行走了(2+1)米,写成算式为:
2+1=3(米)
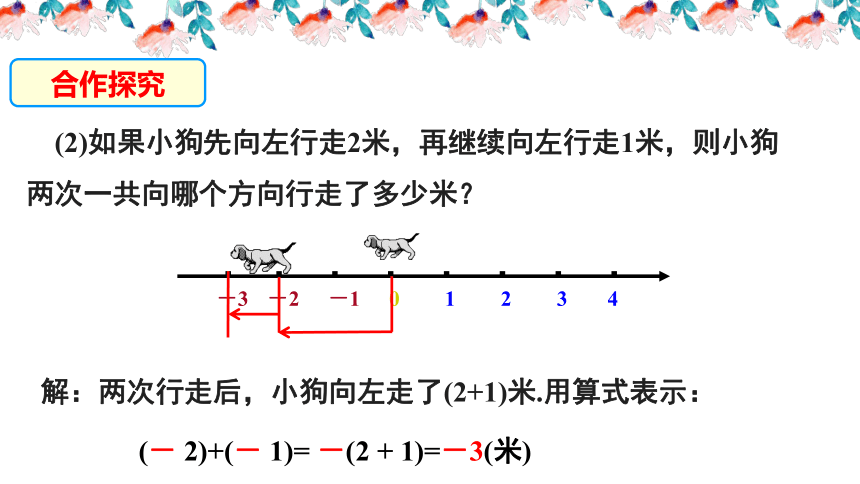
(2)如果小狗先向左行走2米,再继续向左行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
解:两次行走后,小狗向左走了(2+1)米.用算式表示:
(- 2)+(- 1)= -(2 + 1)=-3(米)
合作探究
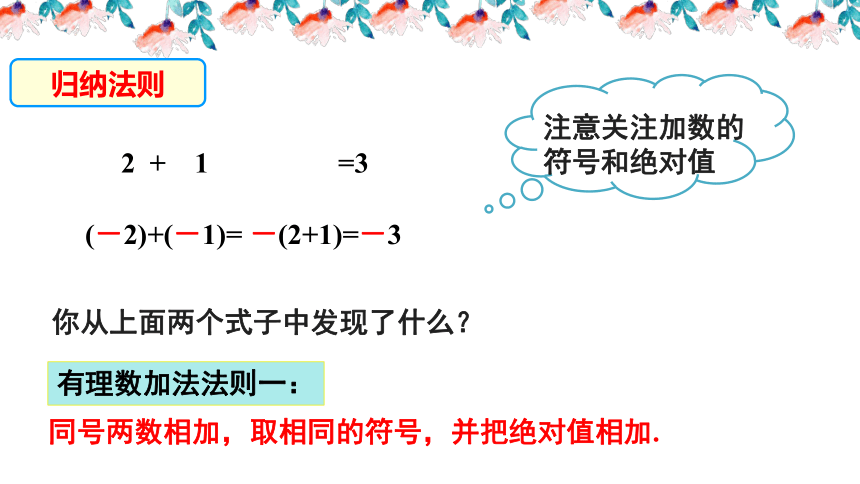
2 + 1 =3
(-2)+(-1)= -(2+1)=-3
你从上面两个式子中发现了什么?
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
归纳法则
注意关注加数的符号和绝对值
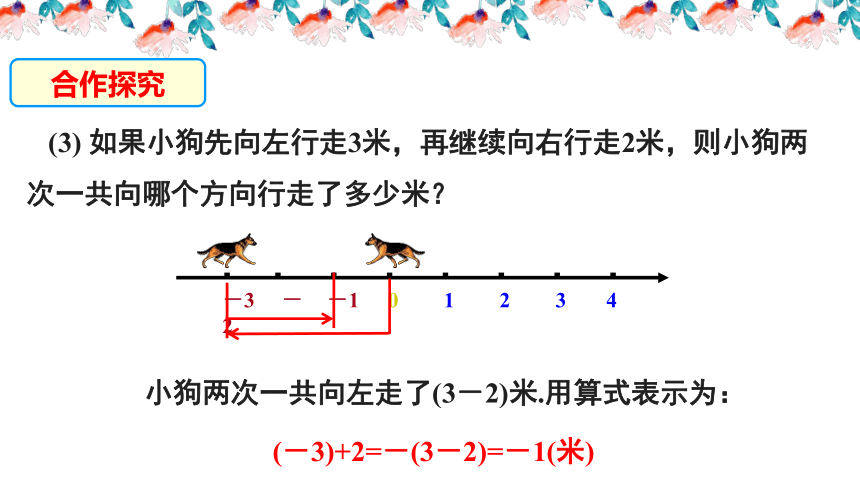
(3) 如果小狗先向左行走3米,再继续向右行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-3 -2
小狗两次一共向左走了(3-2)米.用算式表示为:
(-3)+2=-(3-2)=-1(米)
合作探究
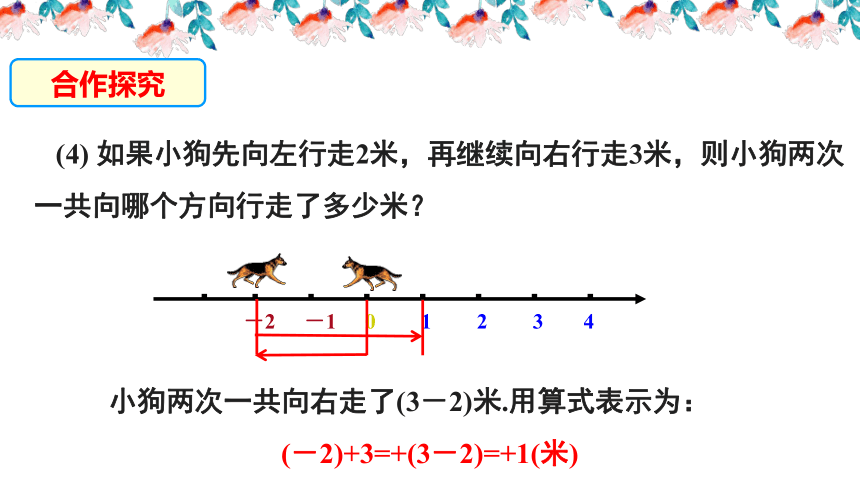
(4) 如果小狗先向左行走2米,再继续向右行走3米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
小狗两次一共向右走了(3-2)米.用算式表示为:
(-2)+3=+(3-2)=+1(米)
合作探究
(5) 如果小狗先向左行走2米,再继续向右行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
(-2)+2= 0(米)
解:小狗一共行走了0米.写成算式为:
合作探究
(-3) + 2= -(3-2)=-1
(-2) + 3 = +(3-2)=+1
(-2) + 2 = (2-2)= 0
你从上面三个式子中发现了什么?
归纳法则
注意关注加数的符号和绝对值
有理数加法法则二:
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
异号两数相加,互为相反数的两个数相加得0;
(6)如果小狗先向左行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
小狗向左行走了3米.写成算式为:
(-3)+0= -3(米)
有理数加法法则三:
一个数同0相加,仍得这个数.
合作探究
有理数加法法则
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值.互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
总结归纳
典例分析
例 计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
(3) 0+(-7);
(4)(-9)+9.
方法总结:1.先看类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
即“一看、二定、三算”.
练习:课本P18 T3
计算:(1)15+(-22);
(2)(-13)+(-8);
(3)(-0.9)+1.5;
课本 第18页 练习
1.用算式表示下面的结果:
(1)温度由-4 ?C上升7?C;(2)收入7元,又支出5元.
课堂练习
2.口算:
(1)(-4)+(-6); (2) 4+(-6); (3)(-4)+6;
(4)(-4)+4; (5)(-4)+14; (6)(-14)+4;
(7) 6+(-6); (8) 0+(-6).
3.用生活实例解释算式5+(-3)= 2;(-5)+(-3)=-8的意义
解:①冬季某天早晨温度为5度,到中午气温下降了3度, 气温为2度;
②取向东为正方向,先向西走了5 km,后又向西走了2 km,一共向西走了8 km.
1.同号两数相加,取相同符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去较小的绝对值,
互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
课堂小结
1. 数a,b表示的点如图所示,则
(1)a + b _____ 0;
(2)a + (-b)_____ 0;
(3)(-a) + b _____ 0;
(4)(-a) + (-b) _____0.
(填“>”“<”或“=”)
拓展延伸
3. 两个有理数的和为负数,则这两个数一定( )
A.都是负数 B.只有一个负数
C.至少有一个负数 D.无法确定
2. 两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
拓展延伸
4. 若a为有理数,则 的值 ( )
A.可能是负数 B.不可能是负数
C.只可能是正数 D.只能是0
拓展延伸
我是火炬手
演示1
+1
-1
(+1) +(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
情境引入
合作探究
(1)如果小狗先向右行走2米,再继续向右行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
解:小狗一共向右行走了(2+1)米,写成算式为:
2+1=3(米)
(2)如果小狗先向左行走2米,再继续向左行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
解:两次行走后,小狗向左走了(2+1)米.用算式表示:
(- 2)+(- 1)= -(2 + 1)=-3(米)
合作探究
2 + 1 =3
(-2)+(-1)= -(2+1)=-3
你从上面两个式子中发现了什么?
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
归纳法则
注意关注加数的符号和绝对值
(3) 如果小狗先向左行走3米,再继续向右行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-3 -2
小狗两次一共向左走了(3-2)米.用算式表示为:
(-3)+2=-(3-2)=-1(米)
合作探究
(4) 如果小狗先向左行走2米,再继续向右行走3米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
小狗两次一共向右走了(3-2)米.用算式表示为:
(-2)+3=+(3-2)=+1(米)
合作探究
(5) 如果小狗先向左行走2米,再继续向右行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
(-2)+2= 0(米)
解:小狗一共行走了0米.写成算式为:
合作探究
(-3) + 2= -(3-2)=-1
(-2) + 3 = +(3-2)=+1
(-2) + 2 = (2-2)= 0
你从上面三个式子中发现了什么?
归纳法则
注意关注加数的符号和绝对值
有理数加法法则二:
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
异号两数相加,互为相反数的两个数相加得0;
(6)如果小狗先向左行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
小狗向左行走了3米.写成算式为:
(-3)+0= -3(米)
有理数加法法则三:
一个数同0相加,仍得这个数.
合作探究
有理数加法法则
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值.互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
总结归纳
典例分析
例 计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
(3) 0+(-7);
(4)(-9)+9.
方法总结:1.先看类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
即“一看、二定、三算”.
练习:课本P18 T3
计算:(1)15+(-22);
(2)(-13)+(-8);
(3)(-0.9)+1.5;
课本 第18页 练习
1.用算式表示下面的结果:
(1)温度由-4 ?C上升7?C;(2)收入7元,又支出5元.
课堂练习
2.口算:
(1)(-4)+(-6); (2) 4+(-6); (3)(-4)+6;
(4)(-4)+4; (5)(-4)+14; (6)(-14)+4;
(7) 6+(-6); (8) 0+(-6).
3.用生活实例解释算式5+(-3)= 2;(-5)+(-3)=-8的意义
解:①冬季某天早晨温度为5度,到中午气温下降了3度, 气温为2度;
②取向东为正方向,先向西走了5 km,后又向西走了2 km,一共向西走了8 km.
1.同号两数相加,取相同符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去较小的绝对值,
互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
课堂小结
1. 数a,b表示的点如图所示,则
(1)a + b _____ 0;
(2)a + (-b)_____ 0;
(3)(-a) + b _____ 0;
(4)(-a) + (-b) _____0.
(填“>”“<”或“=”)
拓展延伸
3. 两个有理数的和为负数,则这两个数一定( )
A.都是负数 B.只有一个负数
C.至少有一个负数 D.无法确定
2. 两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
拓展延伸
4. 若a为有理数,则 的值 ( )
A.可能是负数 B.不可能是负数
C.只可能是正数 D.只能是0
拓展延伸
