人教版2021八年级上册数学11.3.2多边形内外角和教案
文档属性
| 名称 | 人教版2021八年级上册数学11.3.2多边形内外角和教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 54.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 09:04:21 | ||
图片预览

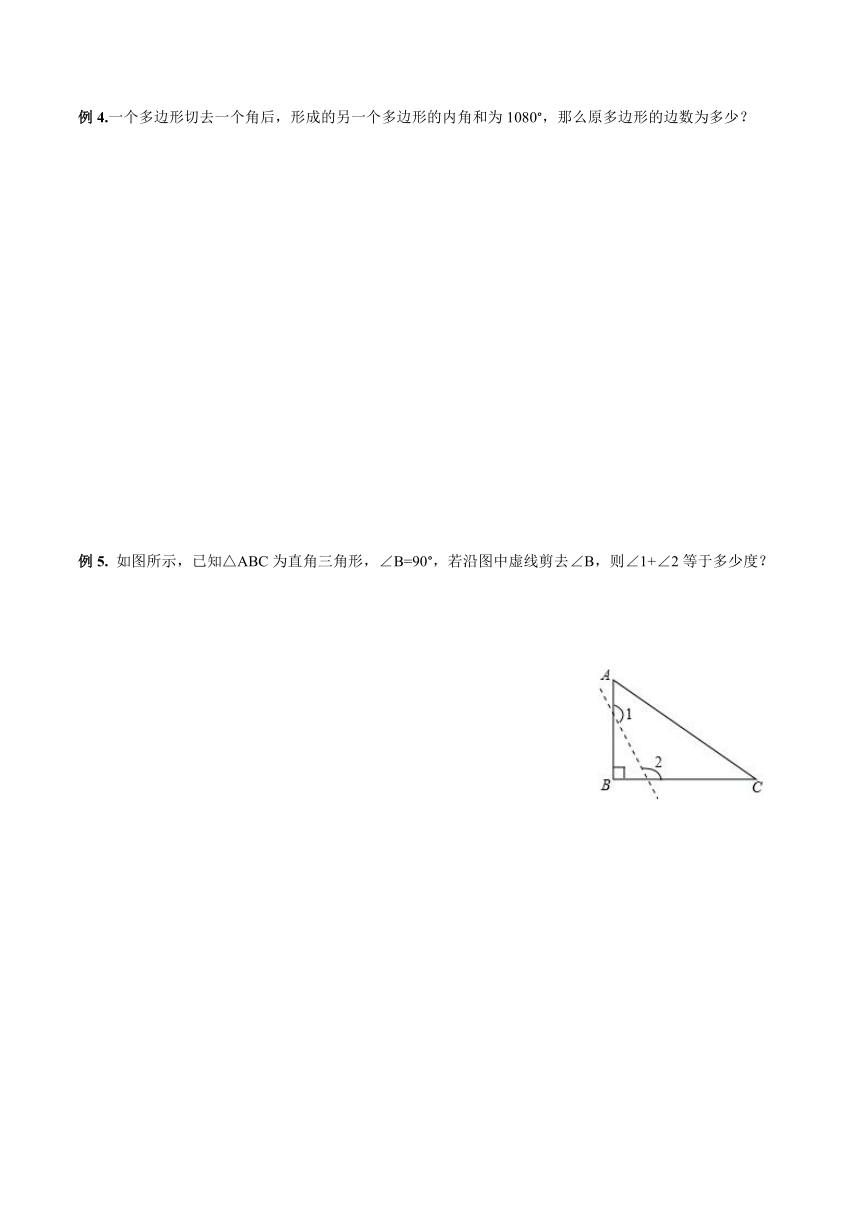
文档简介
多边形内外角和
一、【知识海洋】
1.定义:在平面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
多边形按组成它的线段的条数分成三角形、四边形、五边形……、n边形。
多边形的内角:与三角形类似地,多边形相邻两边组成的角叫做多边形的内角,
如图中的∠A、∠B、∠C、∠D、∠E。
多边形的外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
如图中的∠1是五边形ABCDE的一个外角。
4.正多边形的概念:我们知道,等边三角形、正方形的各个角都相等,各条边都相等,像这样各个角都相等,
各条边都相等的多边形叫做正多边形。
5.多边形的内角和:n边形的内角和等于(n-2)●
180°.
6.多边形的外角和:n边形的外角和等于360°.
7.多边形的对角线:
连接多边形的不相邻的两个顶点的线段,叫做多边形的对角线.
8.观察下面的图形,填空:
从五边形一个顶点出发可以引
对角线,它们将五边形
分成
三角形,五边形的内角和等于
;
从六边形一个顶点出发可以引
对角线,它们将六边形
分成
三角形,六边形的内角和等于
;
从n边形一个顶点出发,可以引
对角线,它们将n边形分成
三角形,n边形的内角和等于
。
二、【经典例题】
例1.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是(
)
A.7
B.10
C.35
D.70
例2.
已知两个多边形的内角和为1800°,且这两个多边形的边数之比为2:5,求这两个多边形的边数.
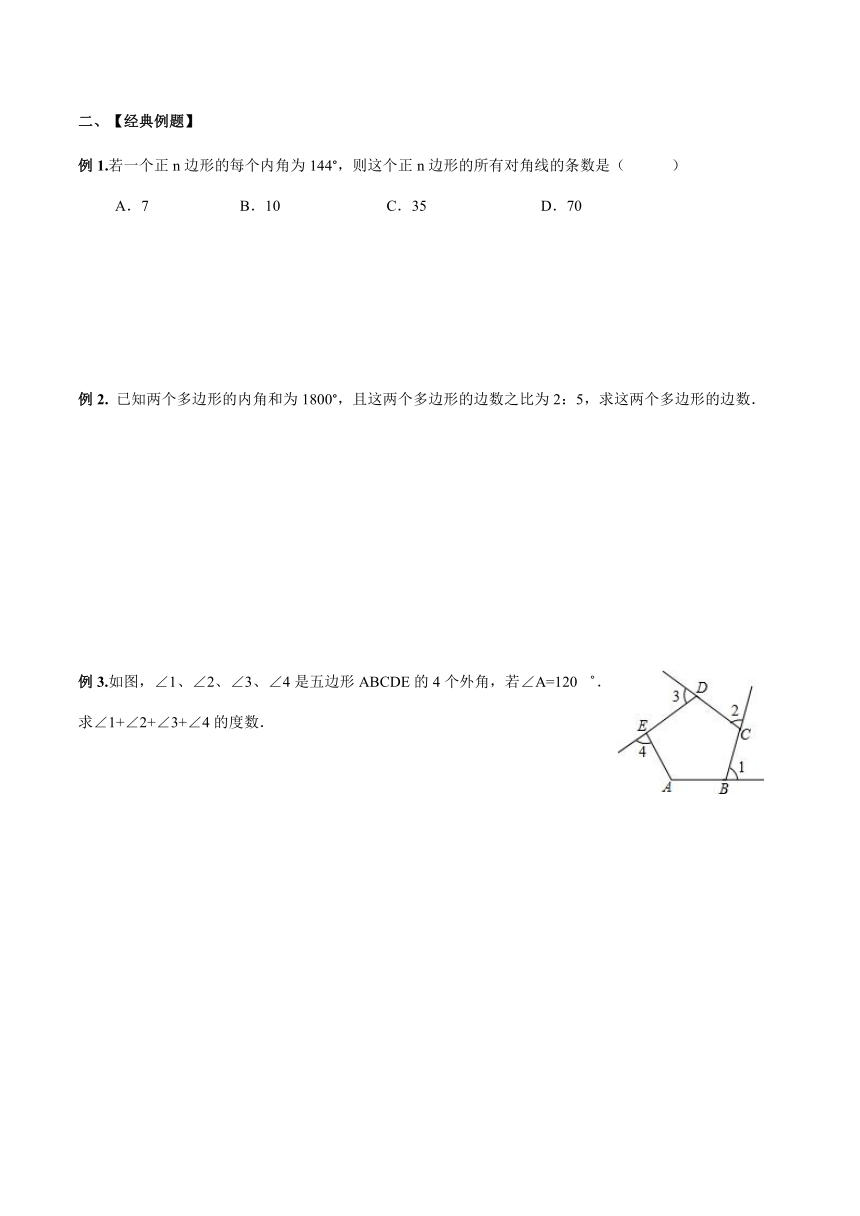
例3.如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角,若∠A=120゜.
求∠1+∠2+∠3+∠4的度数.
例4.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为多少?
例5.
如图所示,已知△ABC为直角三角形,∠B=90°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?
例6.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
例7.
如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,求∠AOB的度数.
例8.
如图,四边形ABCD中,∠A=100°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.
三、【知识巩固】
1.
一个n边形的内角和是1260°,那么n=
.
2.
一个多边形的内角和等于它的外角和,这个多边形是
边形.
3.一个多边形的内角和等于1440°,则此多边形是
边形,它的外角和是
.
4.一个多边形的每一个外角都等于45°,则这个多边形内角和为
度.
5.一个多边形的每一个内角都比相邻的外角的3倍还多20°,求这个多边形对角线的条数。
6.一个多边形的各内角都等于108°,它是几边形?
7.从一个多边形的某个顶点出发,可以作4条对角线,求这个多边形的内角和
8.
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,求∠DFA的度数.
一、【知识海洋】
1.定义:在平面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
多边形按组成它的线段的条数分成三角形、四边形、五边形……、n边形。
多边形的内角:与三角形类似地,多边形相邻两边组成的角叫做多边形的内角,
如图中的∠A、∠B、∠C、∠D、∠E。
多边形的外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
如图中的∠1是五边形ABCDE的一个外角。
4.正多边形的概念:我们知道,等边三角形、正方形的各个角都相等,各条边都相等,像这样各个角都相等,
各条边都相等的多边形叫做正多边形。
5.多边形的内角和:n边形的内角和等于(n-2)●
180°.
6.多边形的外角和:n边形的外角和等于360°.
7.多边形的对角线:
连接多边形的不相邻的两个顶点的线段,叫做多边形的对角线.
8.观察下面的图形,填空:
从五边形一个顶点出发可以引
对角线,它们将五边形
分成
三角形,五边形的内角和等于
;
从六边形一个顶点出发可以引
对角线,它们将六边形
分成
三角形,六边形的内角和等于
;
从n边形一个顶点出发,可以引
对角线,它们将n边形分成
三角形,n边形的内角和等于
。
二、【经典例题】
例1.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是(
)
A.7
B.10
C.35
D.70
例2.
已知两个多边形的内角和为1800°,且这两个多边形的边数之比为2:5,求这两个多边形的边数.
例3.如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角,若∠A=120゜.
求∠1+∠2+∠3+∠4的度数.
例4.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为多少?
例5.
如图所示,已知△ABC为直角三角形,∠B=90°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?
例6.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
例7.
如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,求∠AOB的度数.
例8.
如图,四边形ABCD中,∠A=100°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.
三、【知识巩固】
1.
一个n边形的内角和是1260°,那么n=
.
2.
一个多边形的内角和等于它的外角和,这个多边形是
边形.
3.一个多边形的内角和等于1440°,则此多边形是
边形,它的外角和是
.
4.一个多边形的每一个外角都等于45°,则这个多边形内角和为
度.
5.一个多边形的每一个内角都比相邻的外角的3倍还多20°,求这个多边形对角线的条数。
6.一个多边形的各内角都等于108°,它是几边形?
7.从一个多边形的某个顶点出发,可以作4条对角线,求这个多边形的内角和
8.
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,求∠DFA的度数.
