人教版2021八年级数学上册12.2全等三角形证明学案(无答案)
文档属性
| 名称 | 人教版2021八年级数学上册12.2全等三角形证明学案(无答案) | 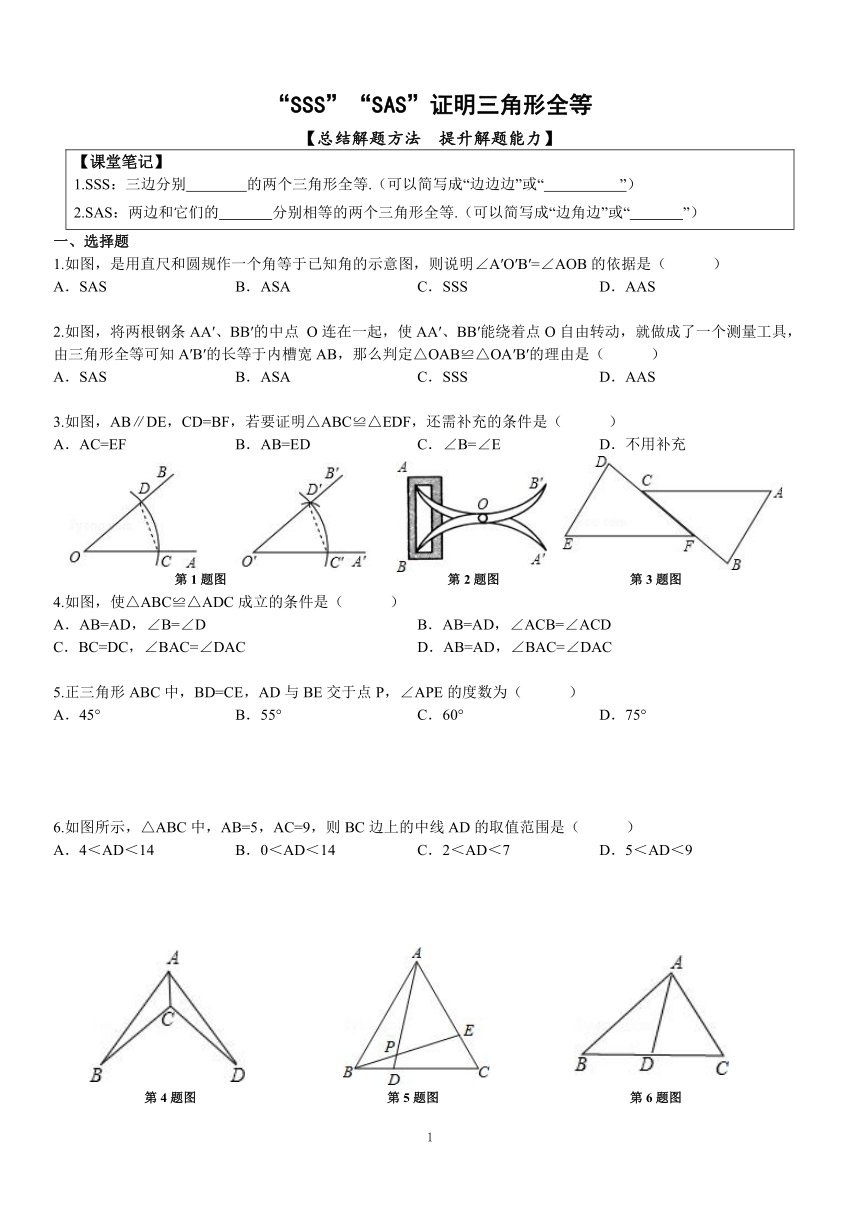 | |
| 格式 | zip | ||
| 文件大小 | 94.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 09:03:44 | ||
图片预览

文档简介
“SSS”“SAS”证明三角形全等
【总结解题方法
提升解题能力】
【课堂笔记】
1.SSS:三边分别
的两个三角形全等.(可以简写成“边边边”或“
”)
2.SAS:两边和它们的
分别相等的两个三角形全等.(可以简写成“边角边”或“
”)
一、选择题
1.如图,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是(
)
A.SAS
B.ASA
C.SSS
D.AAS
2.如图,将两根钢条AA′、BB′的中点
O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是(
)
A.SAS
B.ASA
C.SSS
D.AAS
3.如图,AB∥DE,CD=BF,若要证明△ABC≌△EDF,还需补充的条件是(
)
A.AC=EF
B.AB=ED
C.∠B=∠E
D.不用补充
第1题图
第2题图
第3题图
4.如图,使△ABC≌△ADC成立的条件是(
)
A.AB=AD,∠B=∠D
B.AB=AD,∠ACB=∠ACD
C.BC=DC,∠BAC=∠DAC
D.AB=AD,∠BAC=∠DAC
5.正三角形ABC中,BD=CE,AD与BE交于点P,∠APE的度数为(
)
A.45°
B.55°
C.60°
D.75°
6.如图所示,△ABC中,AB=5,AC=9,则BC边上的中线AD的取值范围是(
)
A.4<AD<14
B.0<AD<14
C.2<AD<7
D.5<AD<9
第4题图
第5题图
第6题图
二、填空题
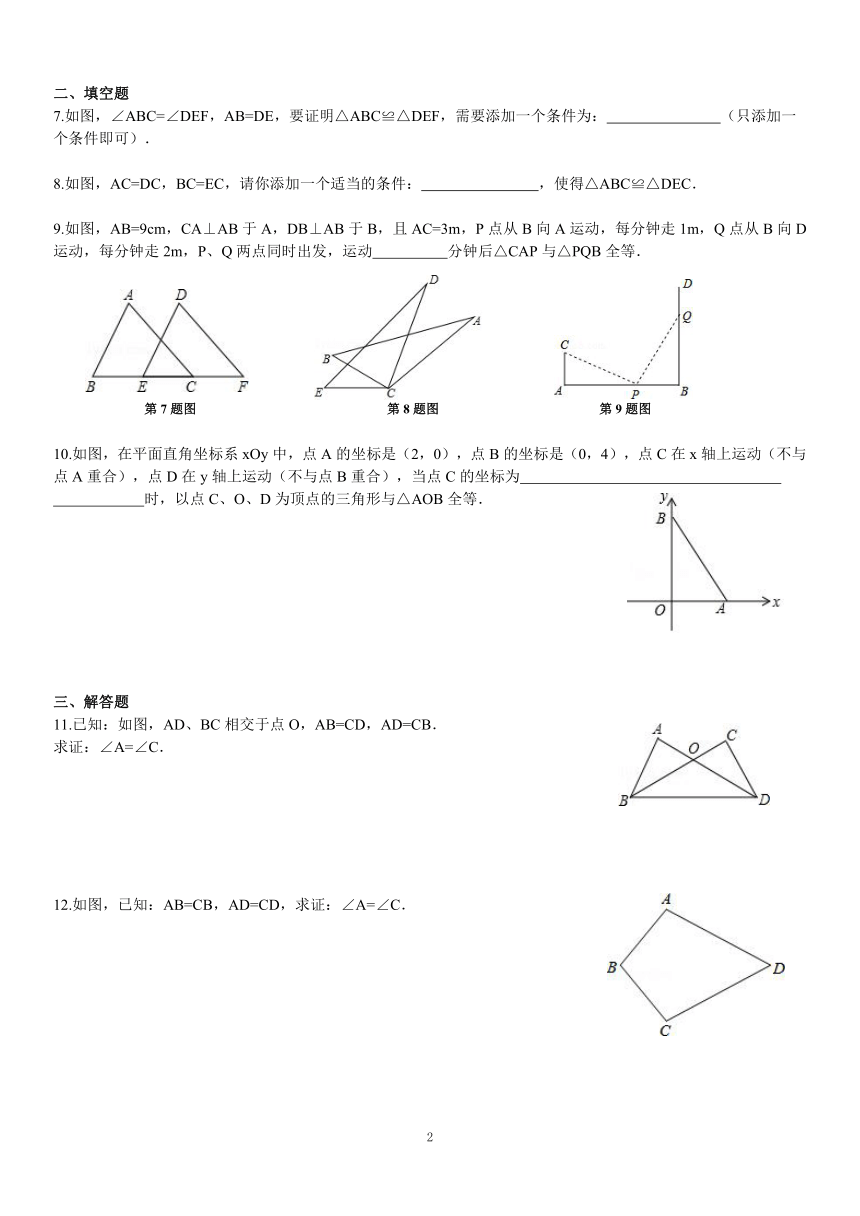
7.如图,∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为:
(只添加一个条件即可).
8.如图,AC=DC,BC=EC,请你添加一个适当的条件:
,使得△ABC≌△DEC.
9.如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后△CAP与△PQB全等.
第7题图
第8题图
第9题图
10.如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在y轴上运动(不与点B重合),当点C的坐标为
时,以点C、O、D为顶点的三角形与△AOB全等.
三、解答题
11.已知:如图,AD、BC相交于点O,AB=CD,AD=CB.
求证:∠A=∠C.
12.如图,已知:AB=CB,AD=CD,求证:∠A=∠C.
13.已知:AB=AD,BC=DE,AC=AE,
(1)试说明:∠EAC=∠BAD.
(2)若∠BAD=42°,求∠EDC的度数.
14.已知如图,E、F是AB上的两点,AE=BF,AC∥BD,且AC=DB,求证:(1)CF=DE.(2)CF∥DE.
15.如图,已知:AD是BC上的中线,且DF=DE.求证:BE∥CF.
16.如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=
cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v
cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
17.如图,已△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;
②点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
(2)若点Q以②的运动速度从点C出发点P以原来运动速度从点B同时出发,都逆时针沿ABC的三边运动,求多长时间点P与点Q第一次在△ABC的哪条边上相遇?
1
【总结解题方法
提升解题能力】
【课堂笔记】
1.SSS:三边分别
的两个三角形全等.(可以简写成“边边边”或“
”)
2.SAS:两边和它们的
分别相等的两个三角形全等.(可以简写成“边角边”或“
”)
一、选择题
1.如图,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是(
)
A.SAS
B.ASA
C.SSS
D.AAS
2.如图,将两根钢条AA′、BB′的中点
O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是(
)
A.SAS
B.ASA
C.SSS
D.AAS
3.如图,AB∥DE,CD=BF,若要证明△ABC≌△EDF,还需补充的条件是(
)
A.AC=EF
B.AB=ED
C.∠B=∠E
D.不用补充
第1题图
第2题图
第3题图
4.如图,使△ABC≌△ADC成立的条件是(
)
A.AB=AD,∠B=∠D
B.AB=AD,∠ACB=∠ACD
C.BC=DC,∠BAC=∠DAC
D.AB=AD,∠BAC=∠DAC
5.正三角形ABC中,BD=CE,AD与BE交于点P,∠APE的度数为(
)
A.45°
B.55°
C.60°
D.75°
6.如图所示,△ABC中,AB=5,AC=9,则BC边上的中线AD的取值范围是(
)
A.4<AD<14
B.0<AD<14
C.2<AD<7
D.5<AD<9
第4题图
第5题图
第6题图
二、填空题
7.如图,∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为:
(只添加一个条件即可).
8.如图,AC=DC,BC=EC,请你添加一个适当的条件:
,使得△ABC≌△DEC.
9.如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后△CAP与△PQB全等.
第7题图
第8题图
第9题图
10.如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在y轴上运动(不与点B重合),当点C的坐标为
时,以点C、O、D为顶点的三角形与△AOB全等.
三、解答题
11.已知:如图,AD、BC相交于点O,AB=CD,AD=CB.
求证:∠A=∠C.
12.如图,已知:AB=CB,AD=CD,求证:∠A=∠C.
13.已知:AB=AD,BC=DE,AC=AE,
(1)试说明:∠EAC=∠BAD.
(2)若∠BAD=42°,求∠EDC的度数.
14.已知如图,E、F是AB上的两点,AE=BF,AC∥BD,且AC=DB,求证:(1)CF=DE.(2)CF∥DE.
15.如图,已知:AD是BC上的中线,且DF=DE.求证:BE∥CF.
16.如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=
cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v
cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
17.如图,已△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;
②点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
(2)若点Q以②的运动速度从点C出发点P以原来运动速度从点B同时出发,都逆时针沿ABC的三边运动,求多长时间点P与点Q第一次在△ABC的哪条边上相遇?
1
