北师大版数学八年级下册1.2.1直角三角形的性质与判定 课件(31张ppt)
文档属性
| 名称 | 北师大版数学八年级下册1.2.1直角三角形的性质与判定 课件(31张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 746.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 00:00:00 | ||
图片预览







文档简介
第一章 三角形的证明
2 直角三角形
课时1 直角三角形的性质与判定
直角三角形中角的关系
直角三角形中边角关系
逆命题和逆定理.(重点、难点)
学习目标
新课导入
三角形的分类
按边分类
按角分类
新课导入
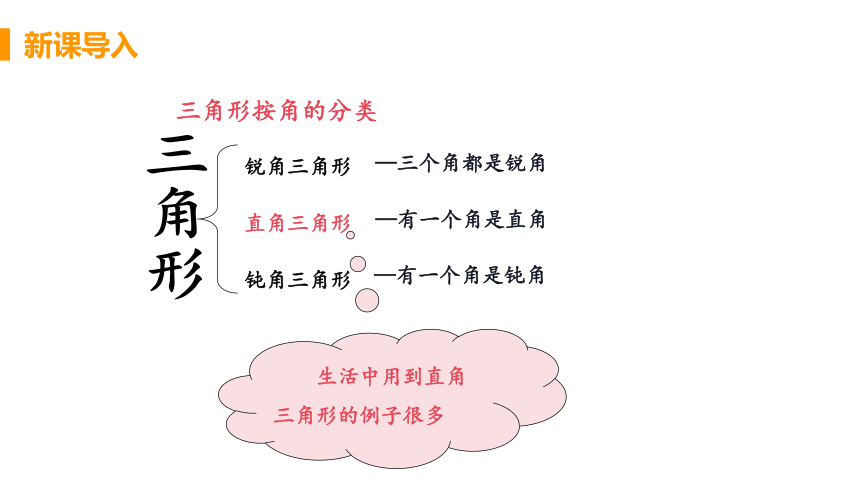
锐角三角形
直角三角形
钝角三角形
—有一个角是钝角
三角形按角的分类
—三个角都是锐角
—有一个角是直角
生活中用到直角三角形的例子很多
三角形
新课讲解
知识点1 直角三角形中角的关系
想一想
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为什么?
新课讲解
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
新课讲解
例
典例分析
如图,在△ABC中,∠C=70°,∠B=30°,AD⊥BC于点D,AE为∠BAC的平分线,求∠DAE的度数.
新课讲解
由题意可知,
∠BAC=180°-∠B-∠C
=180°-30°-70°=80°.
∵AE为∠BAC的平分线,
∴∠CAE=∠BAE= ∠BAC=40°.
∵AD⊥BC,∴∠ADC=90°.
∴∠CAD=90°-∠C=90°-70°=20°.
∴∠DAE=∠CAE-∠CAD=40°-20°=20°.
解:
新课讲解
练一练
1.小明把一副含45°,30°的直角三角尺如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180°
B.210°
C.360°
D.270°
B
新课讲解
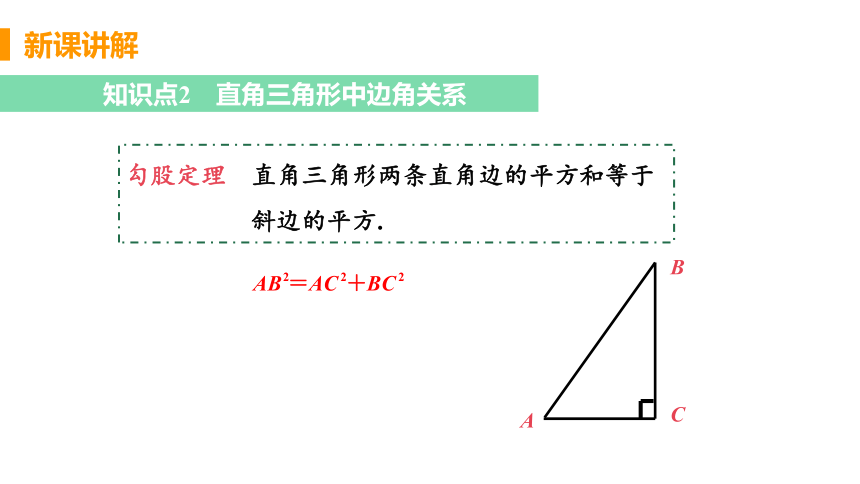
知识点2 直角三角形中边角关系
勾股定理 直角三角形两条直角边的平方和等于
斜边的平方.
A
C
B
新课讲解
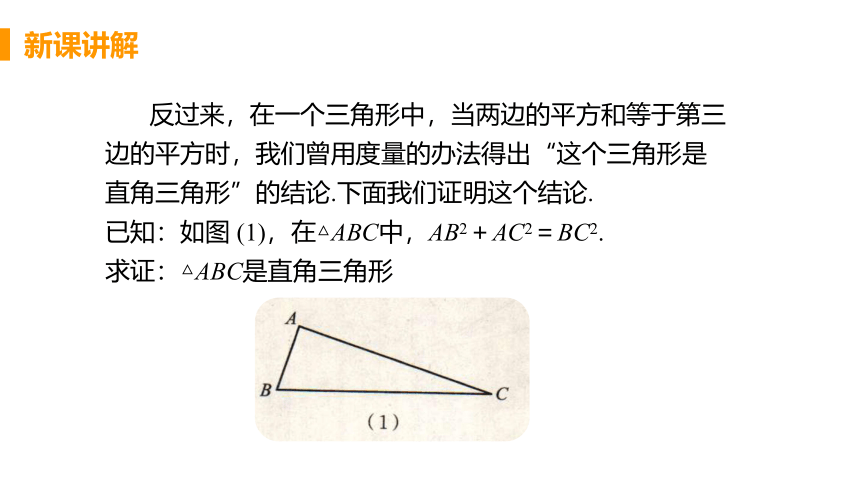
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的办法得出“这个三角形是直角三角形”的结论.下面我们证明这个结论.
已知:如图 (1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形
新课讲解
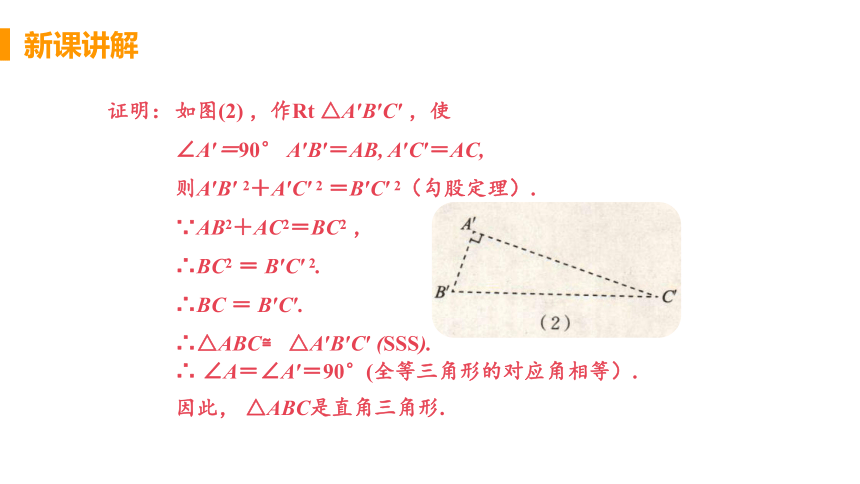
证明:
如图(2) ,作Rt △A′B′C′ ,使
∠A′=90° A′B′=AB, A′C′=AC,
则A′B′ 2+A′C′ 2 =B′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B′C′ 2.
∴BC = B′C′.
∴△ABC≌ △A′B′C′ (SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此, △ABC是直角三角形.
新课讲解
例
典例分析
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A
新课讲解
分析:方法一:
∵∠C=90°,∴AB2=AC2+BC2=92+122=225.
∴AB=15.
过点C作CD⊥AB于点D,设AD=x,则BD=15-x.
在Rt△ACD中,CD2=AC2-AD2=92-x2.
在Rt△BCD中,CD2=BC2-BD2=122-(15-x)2.
∴92-x2=122-(15-x)2,解得x=5.4.
∴CD2=92-5.42=51.84.
∴CD=7.2= ,即点C到AB的距离为 .
新课讲解
方法二:过点C作CD⊥AB于点D,
则S△ABC= AC·BC= AB·CD,
∴AC·BC=AB·CD.又由方法一知AB=15,
∴CD= ,即点C到AB的距离为 .
新课讲解
练一练
1.在△ABC中,已知∠A=∠B=45°,BC=3,求AB的长.
因为∠A=∠B=45°,
所以△ABC为等腰直角三角形.
所以AC=BC=3.
所以
解:
新课讲解
2.已知:在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm. 求证:AB=AC.
如图,
因为AD是BC边上的中线,
所以BD= BC= ×10
=5(cm).
解:
新课讲解
在△ABD中,
因为AB=13 cm,AD=12 cm,BD=5 cm,
所以AB2=AD2+BD2.
所以△ABD为直角三角形.所以AD⊥BC.
在Rt△ADC中,
AC= =13(cm),
所以AB=AC.
新课讲解
知识点3 逆命题和逆定理
观察上面第一个定理和第二个定理,它们的条件和结论之间有怎样的关系?第三个定理和第四个定理呢?与同伴交流.
再观察下面三组命题:
(1)如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
(2)如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
新课讲解
(3)一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
上面每组中两个命题的条件和结论也有类似的关系吗?与同伴交流.
新课讲解
1.在两个命题中,如果一个命题的条件和结论分别
是另一个命题的结论和条件,那么这两个命题称
为互逆命题,其中一个命题称为另一个命题的逆
命题.
2.如果一个定理的逆命题经过证明是真命题,那么
它也是一个定理,其中一个定理称为另一个定理
的逆定理,这两个定理称为互逆定理.
新课讲解
例
典例分析
判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
分析:
根据题目要求,先判断原命题的真假,再将原命题
的题设和结论部分互换,写出原命题的逆命题,最
后判断逆命题的真假.
新课讲解
解:
(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
新课讲解
例
定理“角平分线上的点到角的两边的距离相等”是否有逆定理?请说明理由.
分析:
先写出这个定理的逆命题,再判断逆命题的真假即可.
解:
定理的逆命题:在角的内部,到角两边距离相等的点在
这个角的平分线上.可以证明其为真命题,所以它是原
定理的逆定理.理由如下:
已知:如图,PE⊥OA,
PF⊥OB,垂足分别为E,F,
且PE=PF.
求证:OP是∠AOB的平分线.
新课讲解
证明:
∵PE⊥OA,PF⊥OB,
∴∠OEP=∠OFP=90°.
在Rt△POE和Rt△POF中,由勾股定理易得OE=OF,
∴△POE≌△POF.
∴∠AOP=∠BOP,即OP是∠AOB的平分线.
即在角的内部,到角两边距离相等的点在这个角的
平分线上.
故定理“角平分线上的点到角的两边的距离相 等”
有逆定理.
新课讲解
说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
(1)逆命题:多边形是四边形.原命题真,逆命题假.
(2)逆命题:同旁内角互补,两直线平行.原命题真,
逆命题真.
(3)逆命题:如果 a=0,b=0,那么ab=0. 原命题假,
逆命题真.
解:
练一练
课堂小结
直角三角形角的关系:
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
(2) 勾股定理及其逆定理:
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
勾股定理逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
(3) 互逆命题、互逆定理:
当堂小练
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4
C.5 D.6
C
当堂小练
2.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
B
拓展与延伸
一直角三角形的两边长分别为3和4,则第三边的长为( )
A.5 B.
C. D.5或
D
布置作业
请完成对应习题
2 直角三角形
课时1 直角三角形的性质与判定
直角三角形中角的关系
直角三角形中边角关系
逆命题和逆定理.(重点、难点)
学习目标
新课导入
三角形的分类
按边分类
按角分类
新课导入
锐角三角形
直角三角形
钝角三角形
—有一个角是钝角
三角形按角的分类
—三个角都是锐角
—有一个角是直角
生活中用到直角三角形的例子很多
三角形
新课讲解
知识点1 直角三角形中角的关系
想一想
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为什么?
新课讲解
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
新课讲解
例
典例分析
如图,在△ABC中,∠C=70°,∠B=30°,AD⊥BC于点D,AE为∠BAC的平分线,求∠DAE的度数.
新课讲解
由题意可知,
∠BAC=180°-∠B-∠C
=180°-30°-70°=80°.
∵AE为∠BAC的平分线,
∴∠CAE=∠BAE= ∠BAC=40°.
∵AD⊥BC,∴∠ADC=90°.
∴∠CAD=90°-∠C=90°-70°=20°.
∴∠DAE=∠CAE-∠CAD=40°-20°=20°.
解:
新课讲解
练一练
1.小明把一副含45°,30°的直角三角尺如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180°
B.210°
C.360°
D.270°
B
新课讲解
知识点2 直角三角形中边角关系
勾股定理 直角三角形两条直角边的平方和等于
斜边的平方.
A
C
B
新课讲解
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的办法得出“这个三角形是直角三角形”的结论.下面我们证明这个结论.
已知:如图 (1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形
新课讲解
证明:
如图(2) ,作Rt △A′B′C′ ,使
∠A′=90° A′B′=AB, A′C′=AC,
则A′B′ 2+A′C′ 2 =B′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B′C′ 2.
∴BC = B′C′.
∴△ABC≌ △A′B′C′ (SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此, △ABC是直角三角形.
新课讲解
例
典例分析
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A
新课讲解
分析:方法一:
∵∠C=90°,∴AB2=AC2+BC2=92+122=225.
∴AB=15.
过点C作CD⊥AB于点D,设AD=x,则BD=15-x.
在Rt△ACD中,CD2=AC2-AD2=92-x2.
在Rt△BCD中,CD2=BC2-BD2=122-(15-x)2.
∴92-x2=122-(15-x)2,解得x=5.4.
∴CD2=92-5.42=51.84.
∴CD=7.2= ,即点C到AB的距离为 .
新课讲解
方法二:过点C作CD⊥AB于点D,
则S△ABC= AC·BC= AB·CD,
∴AC·BC=AB·CD.又由方法一知AB=15,
∴CD= ,即点C到AB的距离为 .
新课讲解
练一练
1.在△ABC中,已知∠A=∠B=45°,BC=3,求AB的长.
因为∠A=∠B=45°,
所以△ABC为等腰直角三角形.
所以AC=BC=3.
所以
解:
新课讲解
2.已知:在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm. 求证:AB=AC.
如图,
因为AD是BC边上的中线,
所以BD= BC= ×10
=5(cm).
解:
新课讲解
在△ABD中,
因为AB=13 cm,AD=12 cm,BD=5 cm,
所以AB2=AD2+BD2.
所以△ABD为直角三角形.所以AD⊥BC.
在Rt△ADC中,
AC= =13(cm),
所以AB=AC.
新课讲解
知识点3 逆命题和逆定理
观察上面第一个定理和第二个定理,它们的条件和结论之间有怎样的关系?第三个定理和第四个定理呢?与同伴交流.
再观察下面三组命题:
(1)如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
(2)如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
新课讲解
(3)一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
上面每组中两个命题的条件和结论也有类似的关系吗?与同伴交流.
新课讲解
1.在两个命题中,如果一个命题的条件和结论分别
是另一个命题的结论和条件,那么这两个命题称
为互逆命题,其中一个命题称为另一个命题的逆
命题.
2.如果一个定理的逆命题经过证明是真命题,那么
它也是一个定理,其中一个定理称为另一个定理
的逆定理,这两个定理称为互逆定理.
新课讲解
例
典例分析
判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
分析:
根据题目要求,先判断原命题的真假,再将原命题
的题设和结论部分互换,写出原命题的逆命题,最
后判断逆命题的真假.
新课讲解
解:
(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
新课讲解
例
定理“角平分线上的点到角的两边的距离相等”是否有逆定理?请说明理由.
分析:
先写出这个定理的逆命题,再判断逆命题的真假即可.
解:
定理的逆命题:在角的内部,到角两边距离相等的点在
这个角的平分线上.可以证明其为真命题,所以它是原
定理的逆定理.理由如下:
已知:如图,PE⊥OA,
PF⊥OB,垂足分别为E,F,
且PE=PF.
求证:OP是∠AOB的平分线.
新课讲解
证明:
∵PE⊥OA,PF⊥OB,
∴∠OEP=∠OFP=90°.
在Rt△POE和Rt△POF中,由勾股定理易得OE=OF,
∴△POE≌△POF.
∴∠AOP=∠BOP,即OP是∠AOB的平分线.
即在角的内部,到角两边距离相等的点在这个角的
平分线上.
故定理“角平分线上的点到角的两边的距离相 等”
有逆定理.
新课讲解
说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
(1)逆命题:多边形是四边形.原命题真,逆命题假.
(2)逆命题:同旁内角互补,两直线平行.原命题真,
逆命题真.
(3)逆命题:如果 a=0,b=0,那么ab=0. 原命题假,
逆命题真.
解:
练一练
课堂小结
直角三角形角的关系:
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
(2) 勾股定理及其逆定理:
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
勾股定理逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
(3) 互逆命题、互逆定理:
当堂小练
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4
C.5 D.6
C
当堂小练
2.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
B
拓展与延伸
一直角三角形的两边长分别为3和4,则第三边的长为( )
A.5 B.
C. D.5或
D
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
