北师大版数学八年级下册1.3.1 线段的垂直平分线 课件(28张)
文档属性
| 名称 | 北师大版数学八年级下册1.3.1 线段的垂直平分线 课件(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 691.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 00:00:00 | ||
图片预览






文档简介
第一章 三角形的证明
3 线段的垂直平分线
课时1 线段的垂直平分线
线段的垂直平分线的性质
线段的垂直平分线的判定.(重点、难点)
学习目标
新课导入
线段是轴对称图形吗?它的对称轴是什么?
什么叫线段的垂直平分线?
新课讲解
知识点1 线段的垂直平分线的性质
探究
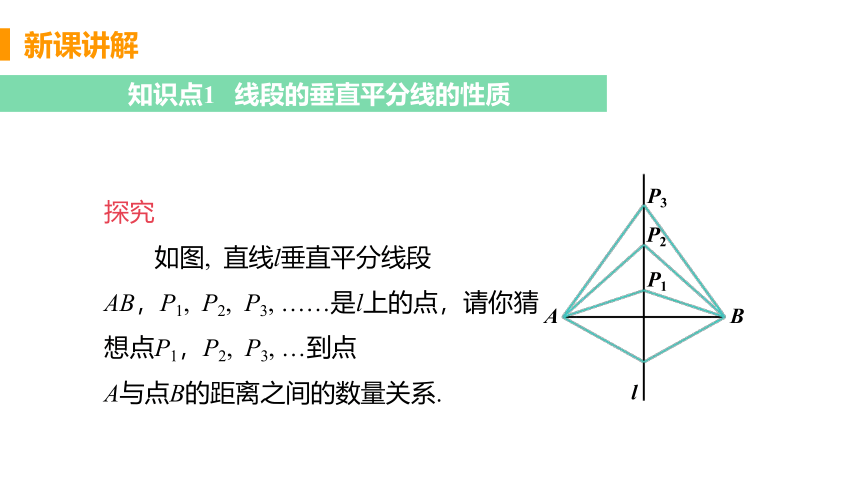
如图, 直线l垂直平分线段
AB,P1, P2, P3, ……是l上的点,请你猜想点P1,P2, P3, …到点
A与点B的距离之间的数量关系.
A
B
l
P1
P2
P3
新课讲解
可以发现,点 P1,P2, P3,…到点A的距离与它们
到点B的距离分别相等.如果把线段AB沿直线l对折,
线段P1A与P1B、线段P2A与P2B、线段 P3A与P3B……
都是重合的,因此它们也分别相等.
新课讲解
线段的垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的
距离相等.利用判定两个三角形全等的方法,也可以
证明这个性质.
新课讲解
例
典例分析
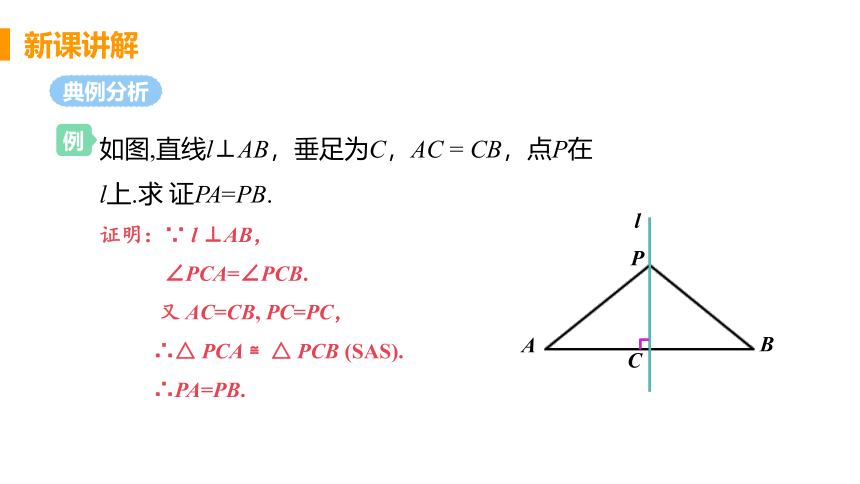
如图,直线l⊥AB,垂足为C,AC = CB,点P在
l上.求 证PA=PB.
证明:∵ l ⊥AB,
∠PCA=∠PCB.
又 AC=CB, PC=PC,
∴△ PCA ≌△ PCB (SAS).
∴PA=PB.
A
B
P
C
l
新课讲解
定理 线段垂直平分线上的点到这条线段两个端点的
距离相等.
新课讲解
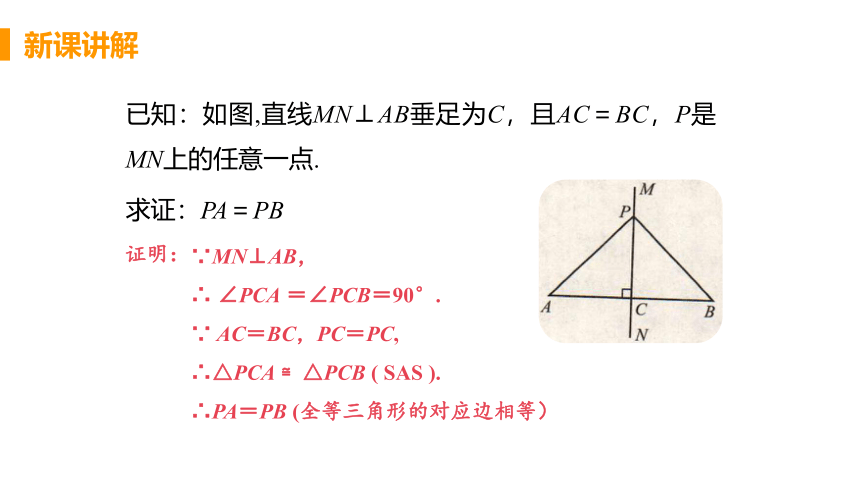
已知:如图,直线MN⊥AB垂足为C,且AC=BC,P是MN上的任意一点.
求证:PA=PB
∵MN⊥AB,
∴ ∠PCA =∠PCB=90°.
∵ AC=BC,PC=PC,
∴△PCA ≌△PCB ( SAS ).
∴PA=PB (全等三角形的对应边相等)
证明:
新课讲解
1.性质:线段垂直平分线上的点到这条线段两个端点
的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端点的距离相等.
表达方式:如图,l⊥AB,AO=BO,点P在l上,则
AP=BP.
2.作用:可用来证明两线段
相等.
新课讲解
例
典例分析
如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD
B.AC平分∠BCD
C.AB=BD
D.△BEC≌△DEC
C
新课讲解
分析:
根据线段垂直平分线的性质得出AB与AD的关系,
结合三角形全等进行逐一验证四个选择项求解.
∵AC垂直平分BD,∴AB=AD,BC=CD.
又∵AC=AC,
∴△ABC≌△ADC.
∴∠BAC=∠DAC,∠BCA=∠DCA.
又∵BC=DC,CE=CE,
∴△BEC≌△DEC.
∴选项A,B,D正确.
新课讲解
例
典例分析
如图,在△ABC中,AC=5,AB的垂直平分线DE交AB,AC于点E,D.
(1)若△BCD的周长为8,求BC的长;
(2) 若BC=4,求△BCD的周长.
分析:
由DE是AB的垂直平分线,得AD=BD,所以BD与CD的长度和等于AC的长,所以由△BCD的周长可求BC的长,同样由BC的长也可求△BCD的周长.
新课讲解
解:
∵DE是AB的垂直平分线,
∴AD=BD.
∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.
新课讲解
例
典例分析
如图,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD=________.
分析:
在△ABC中,∵∠B=90°,
∠A=40°,
∴∠ACB=50°.
∵MN是线段AC的垂直平分线,
∴DC=DA.
∴∠DCE=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.
10°
新课讲解
练一练
1.已知:如图,AB是线段CD的垂直平分线,E,F是AB上的两点. 求证∠ECF=∠EDF.
证明:
因为AB是线段CD的垂直平分线,
所以EC=ED,FC=FD.
在△ECF和△EDF中,
所以△ECF≌△EDF(SSS).
所以∠ECF=∠EDF.
新课讲解
2.如图,在△ABC中,AD垂直平分BC,AC=CE,点B,D,C,E在同一直线上,则AB+BD与DE的关系是( )
A.AB+DB>DE
B.AB+DB<DE
C.AB+DB=DE
D.不能确定
C
新课讲解
知识点2 线段的垂直平分线的判定
想一想
你能写出上面这个定理的逆命题吗?它是真命题吗?
如果是,请你加以 证明.
新课讲解
定理 到一条线段两个端点距离相等的点,在这
条线段的垂直平分线上
新课讲解
1.判定:到一条线段两个端点距离相等的点,在这条线
段的垂直平分线上.
2.条件:点到线段两端点距离相等;
3.结论:点在线段垂直平分线上.
4.表达方式:如图,∵PA=PB,∴点P在线段AB的垂
直平分线上.
5.作用:
①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
新课讲解
例
典例分析
已知:如图,在△ABC中,AB=AC是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
新课讲解
证明:
∵ AB=AC,
∴点A在线段BC的垂直平分线上(到一条线段
两个端点距离相等的点,在这条线段的垂直
平分线上).
同理,点O在线段BC的垂直平分线上.
∴直线AO是线段BC的垂直平分线(两点确定
一条直线).
新课讲解
练一练
如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
A
课堂小结
线段:在线段垂直平分线上的点到线段两个端点
距离都相等.
判定:与线段两个端点距离相等的点都在线段的
垂直平分线上.
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离
相等的所有点的集合.
当堂小练
1.如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD等于( )
A.3
B.4
C.4.8
D.5
D
当堂小练
2.如图,已知AC⊥BC,BD⊥AD,AC,BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④点O在线段AB的垂直平分线上.
其中正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④
D
拓展与延伸
在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到的锐角为50°,则∠B=__________.
70°或20°
分析:分情况讨论:如果△ABC是锐角三角形,如图①所示,可得∠A=40°,所以∠B=∠C=70°;如果△ABC是钝角三角形,如图②所示,可得∠EAB=40°,所以∠B=∠C=20°.故∠B=70°或20°.
布置作业
请完成对应习题
3 线段的垂直平分线
课时1 线段的垂直平分线
线段的垂直平分线的性质
线段的垂直平分线的判定.(重点、难点)
学习目标
新课导入
线段是轴对称图形吗?它的对称轴是什么?
什么叫线段的垂直平分线?
新课讲解
知识点1 线段的垂直平分线的性质
探究
如图, 直线l垂直平分线段
AB,P1, P2, P3, ……是l上的点,请你猜想点P1,P2, P3, …到点
A与点B的距离之间的数量关系.
A
B
l
P1
P2
P3
新课讲解
可以发现,点 P1,P2, P3,…到点A的距离与它们
到点B的距离分别相等.如果把线段AB沿直线l对折,
线段P1A与P1B、线段P2A与P2B、线段 P3A与P3B……
都是重合的,因此它们也分别相等.
新课讲解
线段的垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的
距离相等.利用判定两个三角形全等的方法,也可以
证明这个性质.
新课讲解
例
典例分析
如图,直线l⊥AB,垂足为C,AC = CB,点P在
l上.求 证PA=PB.
证明:∵ l ⊥AB,
∠PCA=∠PCB.
又 AC=CB, PC=PC,
∴△ PCA ≌△ PCB (SAS).
∴PA=PB.
A
B
P
C
l
新课讲解
定理 线段垂直平分线上的点到这条线段两个端点的
距离相等.
新课讲解
已知:如图,直线MN⊥AB垂足为C,且AC=BC,P是MN上的任意一点.
求证:PA=PB
∵MN⊥AB,
∴ ∠PCA =∠PCB=90°.
∵ AC=BC,PC=PC,
∴△PCA ≌△PCB ( SAS ).
∴PA=PB (全等三角形的对应边相等)
证明:
新课讲解
1.性质:线段垂直平分线上的点到这条线段两个端点
的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端点的距离相等.
表达方式:如图,l⊥AB,AO=BO,点P在l上,则
AP=BP.
2.作用:可用来证明两线段
相等.
新课讲解
例
典例分析
如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD
B.AC平分∠BCD
C.AB=BD
D.△BEC≌△DEC
C
新课讲解
分析:
根据线段垂直平分线的性质得出AB与AD的关系,
结合三角形全等进行逐一验证四个选择项求解.
∵AC垂直平分BD,∴AB=AD,BC=CD.
又∵AC=AC,
∴△ABC≌△ADC.
∴∠BAC=∠DAC,∠BCA=∠DCA.
又∵BC=DC,CE=CE,
∴△BEC≌△DEC.
∴选项A,B,D正确.
新课讲解
例
典例分析
如图,在△ABC中,AC=5,AB的垂直平分线DE交AB,AC于点E,D.
(1)若△BCD的周长为8,求BC的长;
(2) 若BC=4,求△BCD的周长.
分析:
由DE是AB的垂直平分线,得AD=BD,所以BD与CD的长度和等于AC的长,所以由△BCD的周长可求BC的长,同样由BC的长也可求△BCD的周长.
新课讲解
解:
∵DE是AB的垂直平分线,
∴AD=BD.
∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.
新课讲解
例
典例分析
如图,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD=________.
分析:
在△ABC中,∵∠B=90°,
∠A=40°,
∴∠ACB=50°.
∵MN是线段AC的垂直平分线,
∴DC=DA.
∴∠DCE=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.
10°
新课讲解
练一练
1.已知:如图,AB是线段CD的垂直平分线,E,F是AB上的两点. 求证∠ECF=∠EDF.
证明:
因为AB是线段CD的垂直平分线,
所以EC=ED,FC=FD.
在△ECF和△EDF中,
所以△ECF≌△EDF(SSS).
所以∠ECF=∠EDF.
新课讲解
2.如图,在△ABC中,AD垂直平分BC,AC=CE,点B,D,C,E在同一直线上,则AB+BD与DE的关系是( )
A.AB+DB>DE
B.AB+DB<DE
C.AB+DB=DE
D.不能确定
C
新课讲解
知识点2 线段的垂直平分线的判定
想一想
你能写出上面这个定理的逆命题吗?它是真命题吗?
如果是,请你加以 证明.
新课讲解
定理 到一条线段两个端点距离相等的点,在这
条线段的垂直平分线上
新课讲解
1.判定:到一条线段两个端点距离相等的点,在这条线
段的垂直平分线上.
2.条件:点到线段两端点距离相等;
3.结论:点在线段垂直平分线上.
4.表达方式:如图,∵PA=PB,∴点P在线段AB的垂
直平分线上.
5.作用:
①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
新课讲解
例
典例分析
已知:如图,在△ABC中,AB=AC是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
新课讲解
证明:
∵ AB=AC,
∴点A在线段BC的垂直平分线上(到一条线段
两个端点距离相等的点,在这条线段的垂直
平分线上).
同理,点O在线段BC的垂直平分线上.
∴直线AO是线段BC的垂直平分线(两点确定
一条直线).
新课讲解
练一练
如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
A
课堂小结
线段:在线段垂直平分线上的点到线段两个端点
距离都相等.
判定:与线段两个端点距离相等的点都在线段的
垂直平分线上.
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离
相等的所有点的集合.
当堂小练
1.如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD等于( )
A.3
B.4
C.4.8
D.5
D
当堂小练
2.如图,已知AC⊥BC,BD⊥AD,AC,BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④点O在线段AB的垂直平分线上.
其中正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④
D
拓展与延伸
在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到的锐角为50°,则∠B=__________.
70°或20°
分析:分情况讨论:如果△ABC是锐角三角形,如图①所示,可得∠A=40°,所以∠B=∠C=70°;如果△ABC是钝角三角形,如图②所示,可得∠EAB=40°,所以∠B=∠C=20°.故∠B=70°或20°.
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
