北师大版数学八年级下册1.3.2三角形三边的垂直平分线的性质 课件(22张)
文档属性
| 名称 | 北师大版数学八年级下册1.3.2三角形三边的垂直平分线的性质 课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 551.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:58:33 | ||
图片预览




文档简介
第一章 三角形的证明
3 线段的垂直平分线
课时2 三角形三边的垂直平分线的性质
三角形三边的垂直平分线
线段垂直平分线的作图及应用.(重点、难点)
学习目标
新课导入
线段的垂直平分线的性质与判定的内容是什么?
新课讲解
知识点1 三角形三边的垂直平分线
例
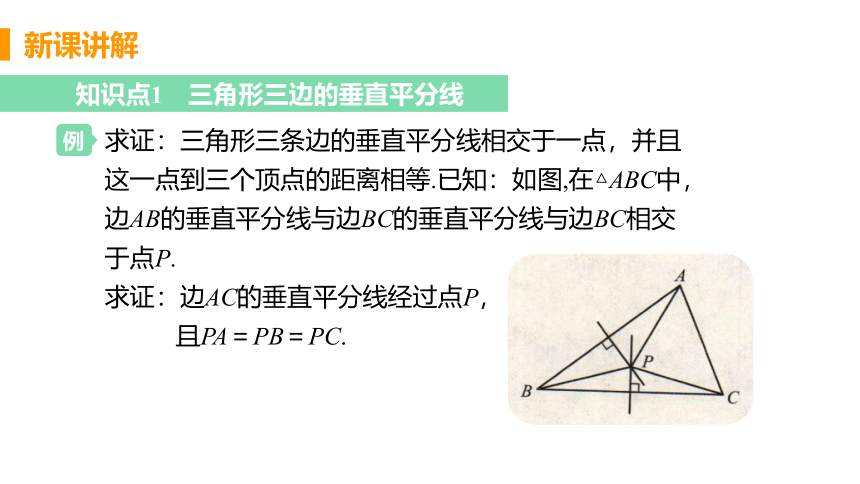
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,
边AB的垂直平分线与边BC的垂直平分线与边BC相交于点P.
求证:边AC的垂直平分线经过点P,
且PA=PB=PC.
新课讲解
∵点P在线段AB的垂直平分线上,
∴ PA = PB(线段垂直平分线上的点到这条线段
两个端点的距离相等).
同理,PB =PC.
∴点P在线段AC的垂直平分线上(到一条线段
两个端点距离相等的点,在这条线段的垂直
平分线上),
即边AC的垂直平分线经过点P.
证明:
新课讲解
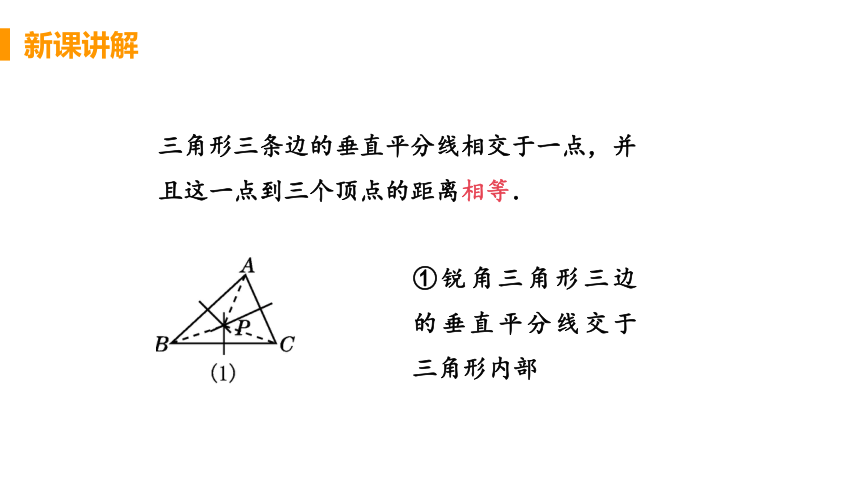
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
①锐角三角形三边的垂直平分线交于三角形内部
新课讲解
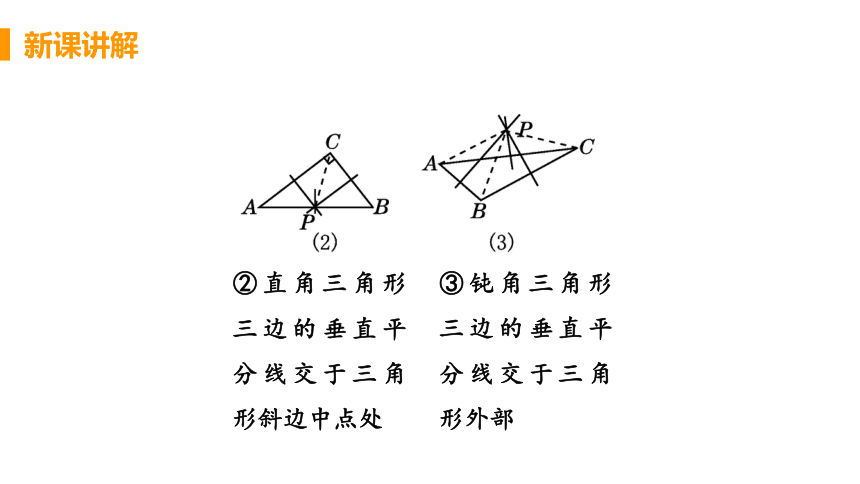
③钝角三角形三边的垂直平分线交于三角形外部
②直角三角形三边的垂直平分线交于三角形斜边中点处
新课讲解
例
典例分析
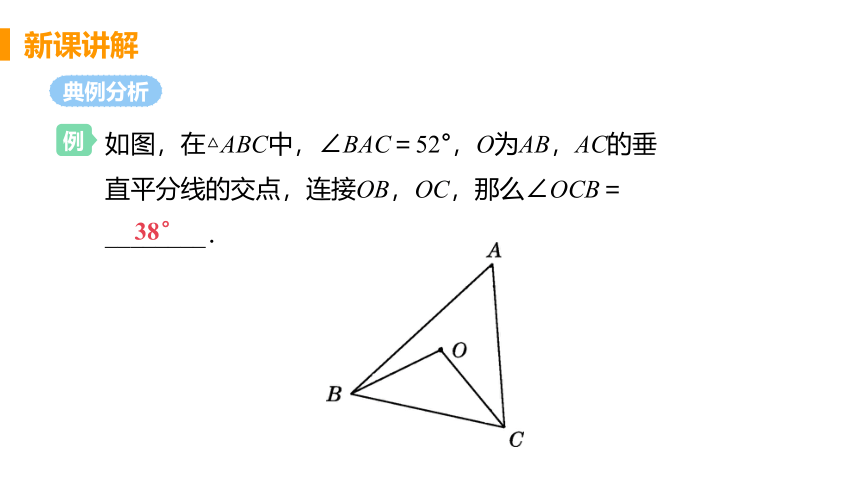
如图,在△ABC中,∠BAC=52°,O为AB,AC的垂直平分线的交点,连接OB,OC,那么∠OCB=________.
38°
新课讲解
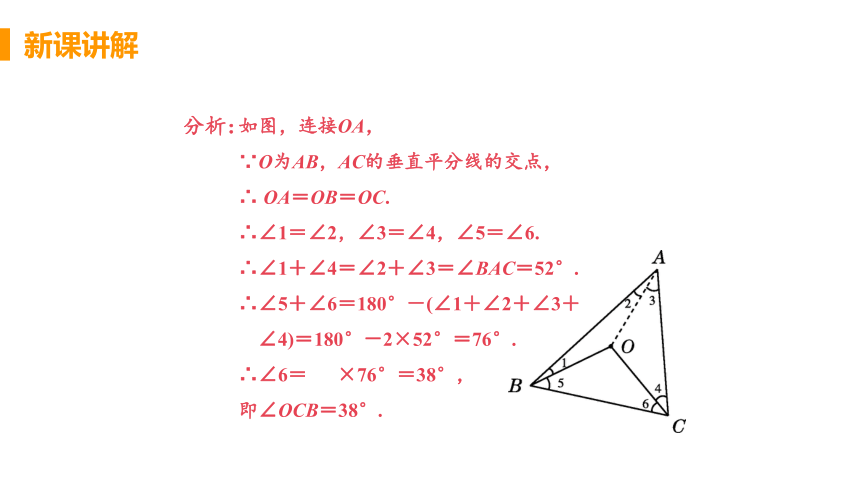
分析:
如图,连接OA,
∵O为AB,AC的垂直平分线的交点,
∴ OA=OB=OC.
∴∠1=∠2,∠3=∠4,∠5=∠6.
∴∠1+∠4=∠2+∠3=∠BAC=52°.
∴∠5+∠6=180°-(∠1+∠2+∠3+
∠4)=180°-2×52°=76°.
∴∠6= ×76°=38°,
即∠OCB=38°.
新课讲解
练一练
如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,请找出图中相等的线段,并求△AEF的周长.
BE=AE,AF=CF.
△AEF的周长为AE+EF+AF
=BE+EF+FC=BC=2.
解:
新课讲解
知识点2 线段垂直平分线的作图及应用
议一议
(1)已知三角形的一条边及这条边上的高,你能画出
满足条件的三角形吗?如果能,能画出几个?所
画出的三角形都全等吗??
(2)已知等腰三角形的底边及底边上的高,你能用尺
规作出满足条件的一 个等腰三角形吗?
新课讲解
用尺规作已知线段的垂直平分线的方法:
已知:线段AB(如图).
求作:线段AB的垂直平分线.
作法:①分别以点A和点B为圆心,
以大于 AB的长为半径画弧,
两弧相交于点C和点D.
②作直线CD,直线CD就是线段
AB的垂直平分线(如图).
新课讲解
例
典例分析
已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.
已知:如图 (1),线段a,h.
求做:△ABC,使AB=AC,且BC=a,高 AD=h.
新课讲解
作法:
(1)作线段BC=a (如图(2)).
(2)作线段BC的垂直平分线l,
交BC于点D.
(3) 在l上作线段DA使DA=h.
(4)连接AB,AC.
△ABC为所求的等腰三角形.
新课讲解
例
典例分析
如图,河流AB的一旁有一村庄P,现要在河流上修建供水站向村庄P供水,要使供水路径最短,求作供水站M的位置.
新课讲解
解:
如图,作法:①以P为圆心,以适当的长度为半
径画弧,交直线AB于C,D两点.
②作线段CD的垂直平分线MN,交CD于M,M点
就是所求作的点.
新课讲解
练一练
如图,已知钝角三角形ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,
交弧①于点D;
步骤3:连接AD,交BC的延长线于点H.
下列叙述正确的是( )
A.BH垂直平分线段AD B.AC平分∠BAD
C.S△ABC=BC·AH D.AB=AD
A
课堂小结
1.三角形三条边的垂直平分线交于同一点,这一点叫
做三角形的外心(三角形外接圆的圆心,以后即可学
到).
2.几种三角形三条边的垂直平分线交点的位置情况:
(1)锐角三角形三边垂直平分线交于三角形内部;
(2)直角三角形三边垂直平分线交于三角形斜边中点;
(3)钝角三角形三边垂直平分线交于三角形外部.
当堂小练
1.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
D
当堂小练
2.已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
D
拓展与延伸
等腰三角形的顶角为100°,其中两边的垂直平分线交于点P,则点P在( )
A.三角形底边上
B.三角形内
C.三角形外
D.点P的位置与三角形边长有关
C
布置作业
请完成对应习题
3 线段的垂直平分线
课时2 三角形三边的垂直平分线的性质
三角形三边的垂直平分线
线段垂直平分线的作图及应用.(重点、难点)
学习目标
新课导入
线段的垂直平分线的性质与判定的内容是什么?
新课讲解
知识点1 三角形三边的垂直平分线
例
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,
边AB的垂直平分线与边BC的垂直平分线与边BC相交于点P.
求证:边AC的垂直平分线经过点P,
且PA=PB=PC.
新课讲解
∵点P在线段AB的垂直平分线上,
∴ PA = PB(线段垂直平分线上的点到这条线段
两个端点的距离相等).
同理,PB =PC.
∴点P在线段AC的垂直平分线上(到一条线段
两个端点距离相等的点,在这条线段的垂直
平分线上),
即边AC的垂直平分线经过点P.
证明:
新课讲解
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
①锐角三角形三边的垂直平分线交于三角形内部
新课讲解
③钝角三角形三边的垂直平分线交于三角形外部
②直角三角形三边的垂直平分线交于三角形斜边中点处
新课讲解
例
典例分析
如图,在△ABC中,∠BAC=52°,O为AB,AC的垂直平分线的交点,连接OB,OC,那么∠OCB=________.
38°
新课讲解
分析:
如图,连接OA,
∵O为AB,AC的垂直平分线的交点,
∴ OA=OB=OC.
∴∠1=∠2,∠3=∠4,∠5=∠6.
∴∠1+∠4=∠2+∠3=∠BAC=52°.
∴∠5+∠6=180°-(∠1+∠2+∠3+
∠4)=180°-2×52°=76°.
∴∠6= ×76°=38°,
即∠OCB=38°.
新课讲解
练一练
如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,请找出图中相等的线段,并求△AEF的周长.
BE=AE,AF=CF.
△AEF的周长为AE+EF+AF
=BE+EF+FC=BC=2.
解:
新课讲解
知识点2 线段垂直平分线的作图及应用
议一议
(1)已知三角形的一条边及这条边上的高,你能画出
满足条件的三角形吗?如果能,能画出几个?所
画出的三角形都全等吗??
(2)已知等腰三角形的底边及底边上的高,你能用尺
规作出满足条件的一 个等腰三角形吗?
新课讲解
用尺规作已知线段的垂直平分线的方法:
已知:线段AB(如图).
求作:线段AB的垂直平分线.
作法:①分别以点A和点B为圆心,
以大于 AB的长为半径画弧,
两弧相交于点C和点D.
②作直线CD,直线CD就是线段
AB的垂直平分线(如图).
新课讲解
例
典例分析
已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.
已知:如图 (1),线段a,h.
求做:△ABC,使AB=AC,且BC=a,高 AD=h.
新课讲解
作法:
(1)作线段BC=a (如图(2)).
(2)作线段BC的垂直平分线l,
交BC于点D.
(3) 在l上作线段DA使DA=h.
(4)连接AB,AC.
△ABC为所求的等腰三角形.
新课讲解
例
典例分析
如图,河流AB的一旁有一村庄P,现要在河流上修建供水站向村庄P供水,要使供水路径最短,求作供水站M的位置.
新课讲解
解:
如图,作法:①以P为圆心,以适当的长度为半
径画弧,交直线AB于C,D两点.
②作线段CD的垂直平分线MN,交CD于M,M点
就是所求作的点.
新课讲解
练一练
如图,已知钝角三角形ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,
交弧①于点D;
步骤3:连接AD,交BC的延长线于点H.
下列叙述正确的是( )
A.BH垂直平分线段AD B.AC平分∠BAD
C.S△ABC=BC·AH D.AB=AD
A
课堂小结
1.三角形三条边的垂直平分线交于同一点,这一点叫
做三角形的外心(三角形外接圆的圆心,以后即可学
到).
2.几种三角形三条边的垂直平分线交点的位置情况:
(1)锐角三角形三边垂直平分线交于三角形内部;
(2)直角三角形三边垂直平分线交于三角形斜边中点;
(3)钝角三角形三边垂直平分线交于三角形外部.
当堂小练
1.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
D
当堂小练
2.已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
D
拓展与延伸
等腰三角形的顶角为100°,其中两边的垂直平分线交于点P,则点P在( )
A.三角形底边上
B.三角形内
C.三角形外
D.点P的位置与三角形边长有关
C
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
