五年级下册数学课件 第三单元《第2课时 长方体和正方体的体积》人教版 (共35张PPT)
文档属性
| 名称 | 五年级下册数学课件 第三单元《第2课时 长方体和正方体的体积》人教版 (共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 07:09:15 | ||
图片预览








文档简介
第三单元
第2课时 长方体和正方体的体积
人教版数学五年级下册
学习目标
1.能正确运用长方体和正方体统一的体积公式。
2.能正确理解长方体和正方体统一的体积公式的推导过程。
同学们,我们知道了每个物体都有一定的体积,我们也知道可以利用数体积单位的方法计算物体的体积。要知道老师手中的这个长方体和正方体的体积,你有什么办法?
导入新知
用将它切成1单位体积的小正方体后数一数的方法
在实际生活中,有许多物体是切不开或不能切的,怎样计算它们的体积呢?它们的体积会和什么有关呢?
1.新课
(1) 任意取出几个1立方厘米的正方体在小组里合作摆出一个长方体,把小组内摆法不同的长方形相关数据填入下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}长
宽
高
小正方体的数量
长方体的体积
合作探究
(2)你是怎么摆的?
(3)观察表格中的数据你发现了什么?
长方体所含体积单位的数量就是长方体的体积。
长方体的体积正好等于长×宽×高的积。
长×宽×高
(4)如何计算长方体的体积?
长方体体积=长×宽×高
用字母表示:V=a×b×h=abh
(5)正方体的体积公式。
根据正方体与长方体的关系,联系长方体的体积公式,想一想正方体的体积应该怎样计算。
正方体的体积=棱长×棱长×棱长
V=a·a·a。
可以写成V=a3,a3表示3个a相乘,读作“a的立方”。
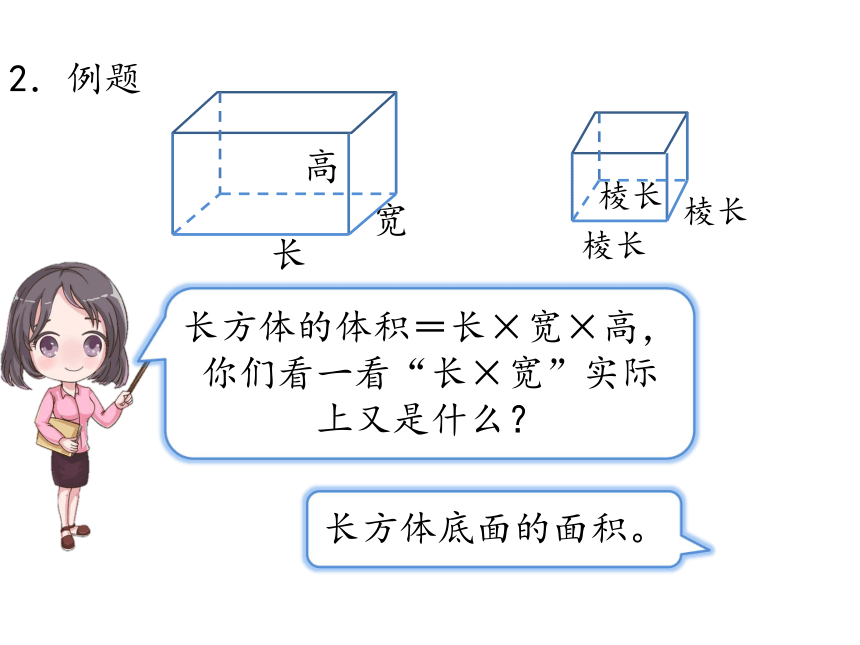
2.例题
长
宽
高
棱长
棱长
棱长
长方体的体积=长×宽×高,你们看一看“长×宽”实际上又是什么?
长方体底面的面积。
正方体的体积=棱长×棱长×棱长,公式中“棱长×棱长”实际又是什么?
正方体底面的面积。
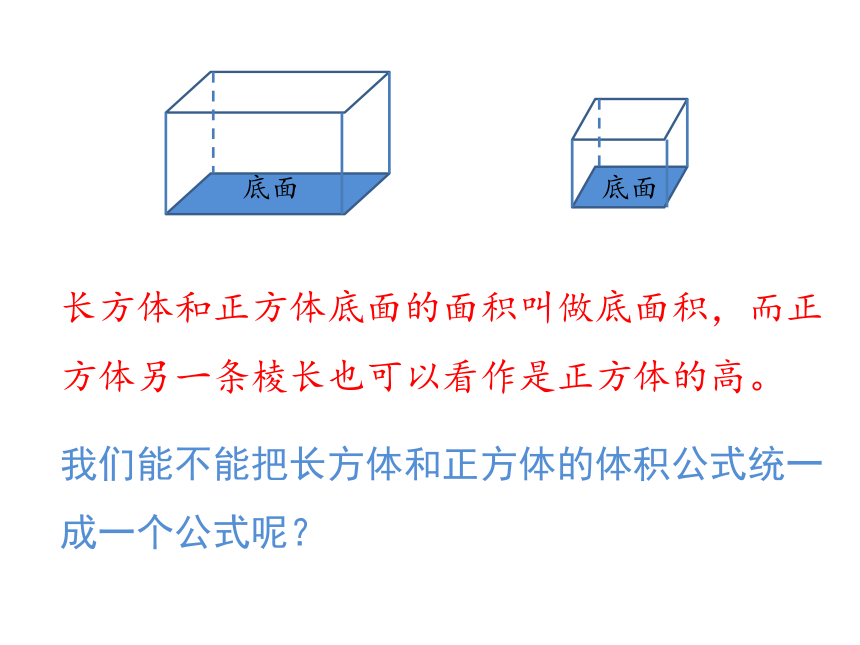
长方体和正方体底面的面积叫做底面积,而正方体另一条棱长也可以看作是正方体的高。
底面
底面
我们能不能把长方体和正方体的体积公式统一成一个公式呢?
长方体和正方体的体积公式能统一成一个公式吗?
长方体(或正方体)的体积=底面积×高
V=Sh
1.一块长方体肥皂的尺寸如下图,它的体积是多少?
15×8×7=840(cm3)
答:它的体积是840cm3。
巩固新知
2.一根长方体木料,长5米,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
3.算一算
43=
4x3=
4+4+4=
82=
8x2=
8+8=
64
12
12
64
16
16
4.建筑工地要挖一个长50m、宽30m、深50cm的长方体挖土坑,一共需要挖出多少方的土?
50x30x0.5=750(m3)
答:一共需要挖出750方的土。
5.一块棱长30cm的正方体冰块,它的体积是多少厘米?
早在夏朝,中国人就已经掌握了存储冰块的技术!
30x30x30=27000(cm3)
答:它的体积是27000cm3。
6.妈妈送给奶奶的长方体形状的生日蛋糕长2dm,宽2dm,高0.6dm。奶奶把它平均分为4块长方体形状的小蛋糕。想一想她是怎样分的,每个人分到多大的一块蛋糕。
解:沿着高把长和宽各平分成2份,就变成了4块长1dm,宽1dm,高0.6dm的小正方体。
1x1x0.6=0.6(立方分米)
答:每个人分到了0.6立方分米的蛋糕。
7.家具厂订购500根方木,每根方木横截面的面积是2.4dm2,长是3m。这些木料一共是多少方?
2.4dm2=0.024(m2)
0.024x3x500=30(平方米)
答:这些木料一共是36平方米。
8.填出下表中长方体或正方体的相关数据。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}底面积
高
体积
32cm2
448cm3
40cm2
5dm
9m
729m3
54cm2
7cm
2000cm2
14cm
0.81cm2
378cm3
9.估一估,量一量。
(1)估计一本数学书的体积是多少?再测量并计算。
(2)估计家里一个长方体家具或者一个房间的体积,再测量并计算。
(3)说一说上面两题你是估计的。怎样估计更准?
课堂练习
课堂总结
通过这节课的学习,你有什么收获?
再 见
第2课时 长方体和正方体的体积
人教版数学五年级下册
学习目标
1.能正确运用长方体和正方体统一的体积公式。
2.能正确理解长方体和正方体统一的体积公式的推导过程。
同学们,我们知道了每个物体都有一定的体积,我们也知道可以利用数体积单位的方法计算物体的体积。要知道老师手中的这个长方体和正方体的体积,你有什么办法?
导入新知
用将它切成1单位体积的小正方体后数一数的方法
在实际生活中,有许多物体是切不开或不能切的,怎样计算它们的体积呢?它们的体积会和什么有关呢?
1.新课
(1) 任意取出几个1立方厘米的正方体在小组里合作摆出一个长方体,把小组内摆法不同的长方形相关数据填入下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}长
宽
高
小正方体的数量
长方体的体积
合作探究
(2)你是怎么摆的?
(3)观察表格中的数据你发现了什么?
长方体所含体积单位的数量就是长方体的体积。
长方体的体积正好等于长×宽×高的积。
长×宽×高
(4)如何计算长方体的体积?
长方体体积=长×宽×高
用字母表示:V=a×b×h=abh
(5)正方体的体积公式。
根据正方体与长方体的关系,联系长方体的体积公式,想一想正方体的体积应该怎样计算。
正方体的体积=棱长×棱长×棱长
V=a·a·a。
可以写成V=a3,a3表示3个a相乘,读作“a的立方”。
2.例题
长
宽
高
棱长
棱长
棱长
长方体的体积=长×宽×高,你们看一看“长×宽”实际上又是什么?
长方体底面的面积。
正方体的体积=棱长×棱长×棱长,公式中“棱长×棱长”实际又是什么?
正方体底面的面积。
长方体和正方体底面的面积叫做底面积,而正方体另一条棱长也可以看作是正方体的高。
底面
底面
我们能不能把长方体和正方体的体积公式统一成一个公式呢?
长方体和正方体的体积公式能统一成一个公式吗?
长方体(或正方体)的体积=底面积×高
V=Sh
1.一块长方体肥皂的尺寸如下图,它的体积是多少?
15×8×7=840(cm3)
答:它的体积是840cm3。
巩固新知
2.一根长方体木料,长5米,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
3.算一算
43=
4x3=
4+4+4=
82=
8x2=
8+8=
64
12
12
64
16
16
4.建筑工地要挖一个长50m、宽30m、深50cm的长方体挖土坑,一共需要挖出多少方的土?
50x30x0.5=750(m3)
答:一共需要挖出750方的土。
5.一块棱长30cm的正方体冰块,它的体积是多少厘米?
早在夏朝,中国人就已经掌握了存储冰块的技术!
30x30x30=27000(cm3)
答:它的体积是27000cm3。
6.妈妈送给奶奶的长方体形状的生日蛋糕长2dm,宽2dm,高0.6dm。奶奶把它平均分为4块长方体形状的小蛋糕。想一想她是怎样分的,每个人分到多大的一块蛋糕。
解:沿着高把长和宽各平分成2份,就变成了4块长1dm,宽1dm,高0.6dm的小正方体。
1x1x0.6=0.6(立方分米)
答:每个人分到了0.6立方分米的蛋糕。
7.家具厂订购500根方木,每根方木横截面的面积是2.4dm2,长是3m。这些木料一共是多少方?
2.4dm2=0.024(m2)
0.024x3x500=30(平方米)
答:这些木料一共是36平方米。
8.填出下表中长方体或正方体的相关数据。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}底面积
高
体积
32cm2
448cm3
40cm2
5dm
9m
729m3
54cm2
7cm
2000cm2
14cm
0.81cm2
378cm3
9.估一估,量一量。
(1)估计一本数学书的体积是多少?再测量并计算。
(2)估计家里一个长方体家具或者一个房间的体积,再测量并计算。
(3)说一说上面两题你是估计的。怎样估计更准?
课堂练习
课堂总结
通过这节课的学习,你有什么收获?
再 见
