人教版数学七年级下册 7.1 平面直角坐标系 同步测试试题(一) (word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 7.1 平面直角坐标系 同步测试试题(一) (word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 92.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 00:00:00 | ||
图片预览



文档简介
平面直角坐标系同步测试试题(一)
一.选择题
1.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y﹣1,﹣x﹣1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2020的坐标为(﹣3,2),设A1(x,y),则x+y的值是( )
A.﹣5
B.﹣1
C.3
D.5
2.已知点P(a﹣5,a+1)在y轴上,则a的值为( )
A.1
B.﹣1
C.﹣5
D.5
3.设点P(x,y)在第二象限,且|x|=5,|y|=2,则点P的坐标是( )
A.(﹣5,2)
B.(5,2)
C.(﹣5,﹣2)
D.(5,﹣2)
4.已知点P(m,n)在第三象限,则点Q(﹣m,|n|)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.下列各点中,在第四象限的是( )
A.(2,0)
B.(﹣2,3)
C.(﹣3,﹣5)
D.(2,﹣5)
6.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一条长为2025个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(﹣1,1)
B.(1,1)
C.(1,0)
D.(﹣1,﹣2)
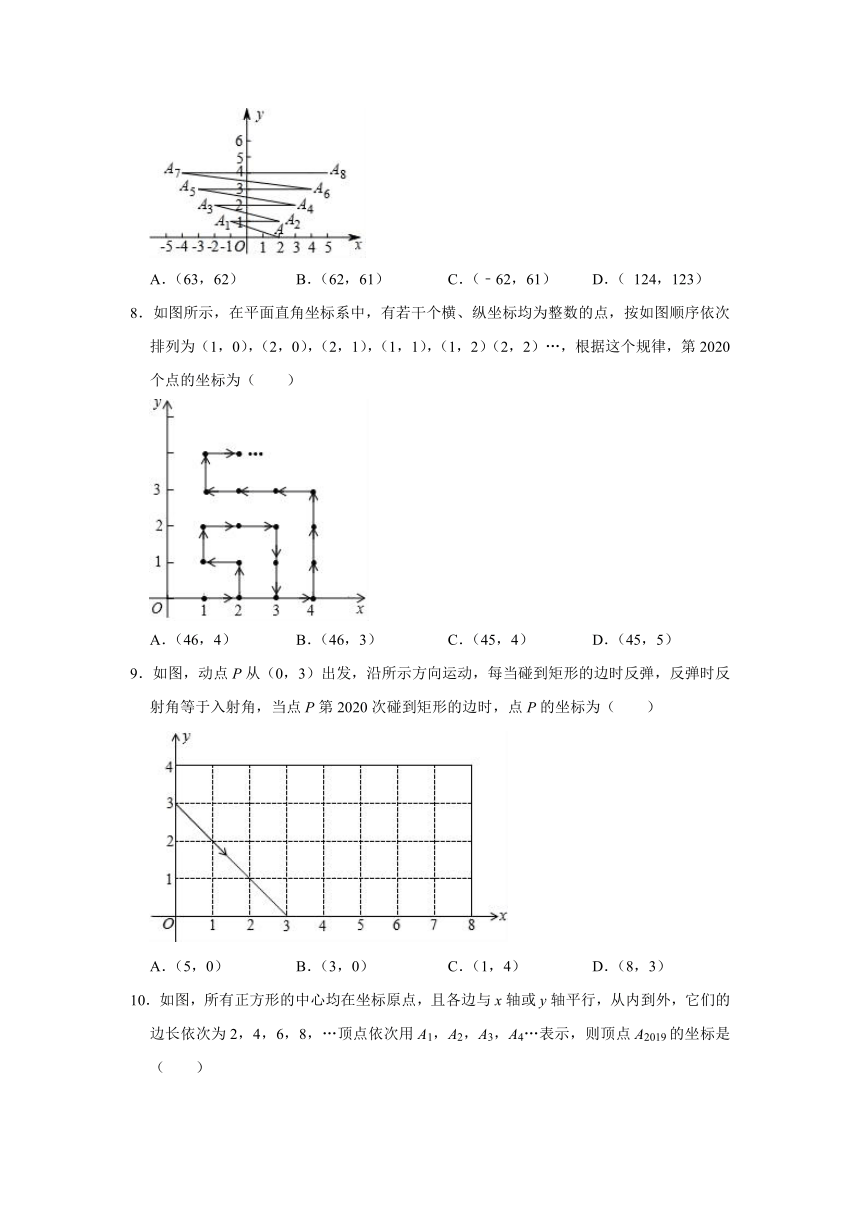
7.如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(﹣1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(﹣2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第124次跳动至A124的坐标( )
A.(63,62)
B.(62,61)
C.(﹣62,61)
D.(
124,123)
8.如图所示,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,按如图顺序依次排列为(1,0),(2,0),(2,1),(1,1),(1,2)(2,2)…,根据这个规律,第2020个点的坐标为( )
A.(46,4)
B.(46,3)
C.(45,4)
D.(45,5)
9.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2020次碰到矩形的边时,点P的坐标为( )
A.(5,0)
B.(3,0)
C.(1,4)
D.(8,3)
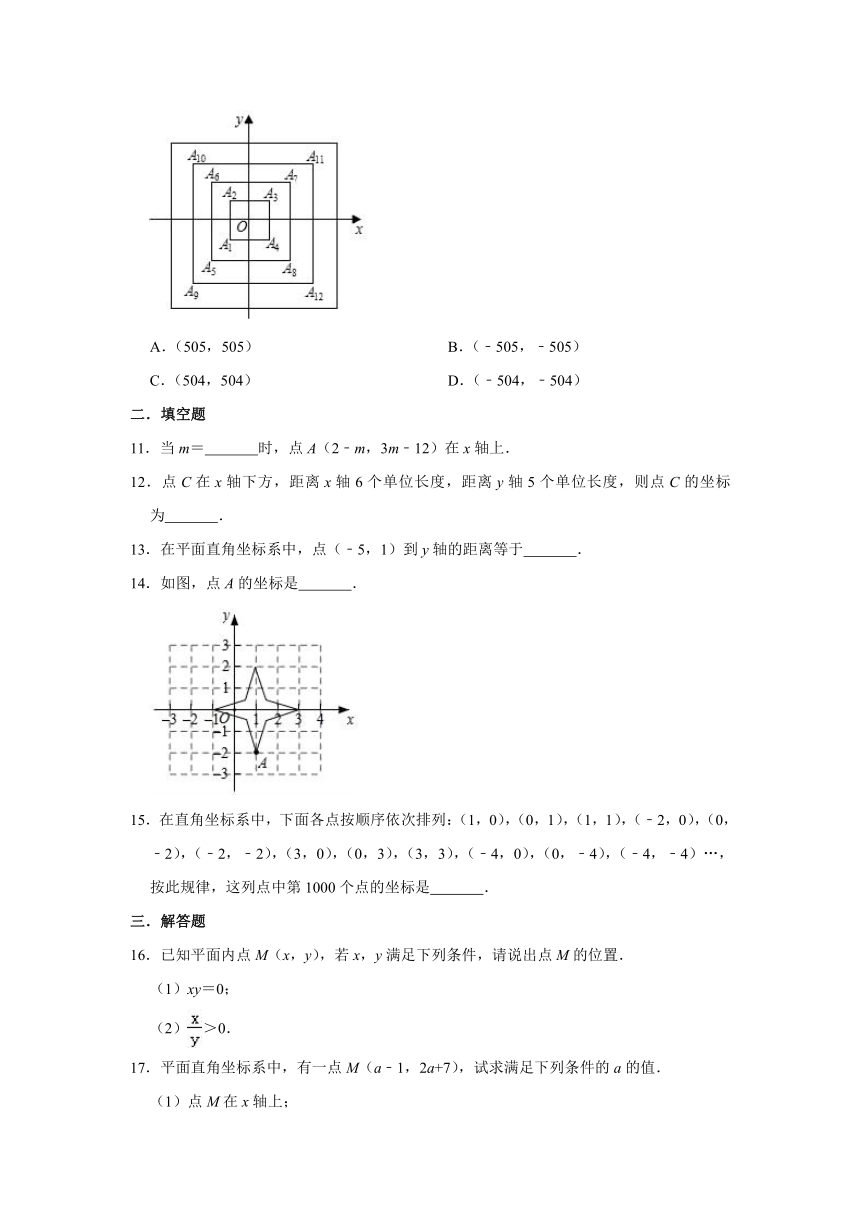
10.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4…表示,则顶点A2019的坐标是( )
A.(505,505)
B.(﹣505,﹣505)
C.(504,504)
D.(﹣504,﹣504)
二.填空题
11.当m=
时,点A(2﹣m,3m﹣12)在x轴上.
12.点C在x轴下方,距离x轴6个单位长度,距离y轴5个单位长度,则点C的坐标为
.
13.在平面直角坐标系中,点(﹣5,1)到y轴的距离等于
.
14.如图,点A的坐标是
.
15.在直角坐标系中,下面各点按顺序依次排列:(1,0),(0,1),(1,1),(﹣2,0),(0,﹣2),(﹣2,﹣2),(3,0),(0,3),(3,3),(﹣4,0),(0,﹣4),(﹣4,﹣4)…,按此规律,这列点中第1000个点的坐标是
.
三.解答题
16.已知平面内点M(x,y),若x,y满足下列条件,请说出点M的位置.
(1)xy=0;
(2)>0.
17.平面直角坐标系中,有一点M(a﹣1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴距离是1.
18.已知当m,n都是实数,且满足2m=8+n时,就称点P(m﹣1,)为“爱心点”.
(1)判断点A(5,3),B(4,8)哪个点为“爱心点”,并说明理由;
(2)若点M(a,2a﹣1)是“爱心点”,请判断点M在第几象限?并说明理由.
19.在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a级关联点”(其中a为常数,且a≠0),例如,点P(1,4)的“2级关联点”为Q(2×1+4,1+2×4),即Q(6,9).
(1)若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为
;
(2)若点P的“5级关联点”的坐标为(9,﹣3),求点P的坐标;
(3)若点P(m﹣1,2m)的“﹣3级关联点”P′位于坐标轴上.求点P′的坐标.
参考答案与试题解析
一.选择题
1.【解答】解:假设A1(1,2),则A2(1,﹣2),A3(﹣3,﹣2),A4(﹣3,2),A5(1,2),…,
∴A4n+1(1,2),A4n+2(1,﹣2),A4n+3(﹣3,﹣2),A4n+4(﹣3,2)(n为自然数).
∵2020=505×4,
∴A2020的坐标为(﹣3,2),
∴A2021(1,2),A1(1,2),
∴x+y=3.
故选:C.
2.【解答】解:∵点P(a﹣5,a+1)在y轴上,
∴a﹣5=0,
解得:a=5.
故选:D.
3.【解答】解:∵点P(x,y)在第二象限,且|x|=5,|y|=2,
∴x=﹣5,y=2,
∴点P的坐标为(﹣5,2).
故选:A.
4.【解答】解:∵点P(m,n)在第三象限,
∴m<0,n<0,
∴﹣m>0,|n|>0,
∴点Q(﹣m,|n|)在第一象限.
故选:A.
5.【解答】解:A、(2,0)在x轴上,不合题意;
B、(﹣2,3)在第二象限,不合题意;
C、(﹣3,﹣5)在第三象限,不合题意;
D、(2,﹣5),在第四象限,符合题意.
故选:D.
6.【解答】解:∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2025÷10=202…5,
∴细线另一端在绕四边形第203圈的第5个单位长度的位置,
即细线另一端所在位置的点的坐标是(﹣1,﹣2).
故选:D.
7.【解答】解:观察发现,第2次跳动至点的坐标是(2,1),
第4次跳动至点的坐标是(3,2),
第6次跳动至点的坐标是(4,3),
第8次跳动至点的坐标是(5,4),
…
第2n次跳动至点的坐标是(n+1,n),
∴第124次跳动至点的坐标是(63,62).
故选:A.
8.【解答】解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…
右下角的点的横坐标为n时,共有n2个,
∵452=2025,45是奇数,
∴第2025个点是(45,0),
第2020个点是(45,5).
故选:D.
9.【解答】解:如图,根据题意得:P0(0,3),P1(3,0),P2(7,4),P3(8,3),P4(5,0),P5(1,4),P6(0,3),P7(3,0),…,
∴点Pn的坐标6次一循环.经过6次反弹后动点回到出发点(0,3),
∵2020÷6=336…4,
∴当点P第2020次碰到矩形的边时为第336个循环组的第4次反弹,
点P的坐标为(5,0).
故选:A.
10.【解答】解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4,(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),
∵2019=504×4+3,
∴A2019(505,505).
故选:A.
二.填空题(共5小题)
11.【解答】解:∵点A(2﹣m,3m﹣12)在x轴上,
∴3m﹣12=0,
解得:m=4,
故答案为:4.
12.【解答】解:由题意,得
x=5或x=﹣5,y=﹣6,
即点的坐标为:(﹣5,﹣6)或(5,﹣6),
故答案为:(﹣5,﹣6)或(5,﹣6).
13.【解答】解:点(﹣5,1)到y轴的距离等于:|﹣5|=5.
故答案为:5.
14.【解答】解:如图所示:点A的坐标是(1,﹣2).
故答案为:(1,﹣2).
15.【解答】解:(1)观察各点规律发现:
第1、4、7、10个点在x轴上,偶数是负号,奇数是正号,
坐标分别(1,0),(﹣2,0),(3,0),(﹣4,0),…,
第2、5、8个点在y轴上,偶数是负号,奇数是正号,
坐标分别(0,1),(0,﹣2),(0,3),…,
第3、6、9个点在一三象限,
坐标分别(1,1),(﹣2,﹣2),(3,3),…,
∵1000÷3=333余1,
∴第1000个点在x轴负半轴上,坐标为(﹣334,0).
故答案为:(﹣334,0).
三.解答题(共4小题)
16.【解答】解:(1)∵xy=0,
∴x=0或y=0或x=0且y=0,
∴点M在y轴或x轴或原点;
(2)∵>0,
∴横纵坐标同号,
∴点M在第一象限或第三象限.
17.【解答】解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=,
所以,当a=时,点M在x轴上;
(2)要使点M在第二象限,a应满足,解得,
所以,当时,点M在第二象限;
(3)要使点M到y轴距离是1,a应满足|a﹣1|=1,解得a=2或a=0,
所以,当a=2或a=0时,点M到y轴距离是1.
18.【解答】解:(1)当A(5,3)时,m﹣1=5,=3,
解得m=6,n=4,
则2m=12,8+n=12,
所以2m=8+n,
所以A(5,3)是“爱心点”;
当B(4,8)时,m﹣1=4,=8,
解得m=5,n=14,显然2m≠8+n,
所以B点不是“爱心点”;
(2)点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“爱心点”,
∴m﹣1=a,=2a﹣1,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1
2a﹣1=﹣3,
∴M(﹣1,﹣3)故点M在第三象限.
19.【解答】解:(1)3×(﹣1)+5=2;﹣1+3×5=14,
∴若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为(2,14).
故答案为:(2,14);
(2)设点P的坐标为(a,b),
由题意可知,
解得:,
∴点P的坐标为(2,﹣1);
(3)∵点P(m﹣1,2m)的“﹣3级关联点”为P′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),①P′位于x轴上,
∴m﹣1+(﹣3)×2m=0,
解得:m=,
∴﹣3(m﹣1)+2m=,
∴P′(,0).
②P′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴P′(0,﹣16).
综上所述,点P′的坐标为(,0)或(0,﹣16).
一.选择题
1.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y﹣1,﹣x﹣1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2020的坐标为(﹣3,2),设A1(x,y),则x+y的值是( )
A.﹣5
B.﹣1
C.3
D.5
2.已知点P(a﹣5,a+1)在y轴上,则a的值为( )
A.1
B.﹣1
C.﹣5
D.5
3.设点P(x,y)在第二象限,且|x|=5,|y|=2,则点P的坐标是( )
A.(﹣5,2)
B.(5,2)
C.(﹣5,﹣2)
D.(5,﹣2)
4.已知点P(m,n)在第三象限,则点Q(﹣m,|n|)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.下列各点中,在第四象限的是( )
A.(2,0)
B.(﹣2,3)
C.(﹣3,﹣5)
D.(2,﹣5)
6.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一条长为2025个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(﹣1,1)
B.(1,1)
C.(1,0)
D.(﹣1,﹣2)
7.如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(﹣1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(﹣2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第124次跳动至A124的坐标( )
A.(63,62)
B.(62,61)
C.(﹣62,61)
D.(
124,123)
8.如图所示,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,按如图顺序依次排列为(1,0),(2,0),(2,1),(1,1),(1,2)(2,2)…,根据这个规律,第2020个点的坐标为( )
A.(46,4)
B.(46,3)
C.(45,4)
D.(45,5)
9.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2020次碰到矩形的边时,点P的坐标为( )
A.(5,0)
B.(3,0)
C.(1,4)
D.(8,3)
10.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4…表示,则顶点A2019的坐标是( )
A.(505,505)
B.(﹣505,﹣505)
C.(504,504)
D.(﹣504,﹣504)
二.填空题
11.当m=
时,点A(2﹣m,3m﹣12)在x轴上.
12.点C在x轴下方,距离x轴6个单位长度,距离y轴5个单位长度,则点C的坐标为
.
13.在平面直角坐标系中,点(﹣5,1)到y轴的距离等于
.
14.如图,点A的坐标是
.
15.在直角坐标系中,下面各点按顺序依次排列:(1,0),(0,1),(1,1),(﹣2,0),(0,﹣2),(﹣2,﹣2),(3,0),(0,3),(3,3),(﹣4,0),(0,﹣4),(﹣4,﹣4)…,按此规律,这列点中第1000个点的坐标是
.
三.解答题
16.已知平面内点M(x,y),若x,y满足下列条件,请说出点M的位置.
(1)xy=0;
(2)>0.
17.平面直角坐标系中,有一点M(a﹣1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴距离是1.
18.已知当m,n都是实数,且满足2m=8+n时,就称点P(m﹣1,)为“爱心点”.
(1)判断点A(5,3),B(4,8)哪个点为“爱心点”,并说明理由;
(2)若点M(a,2a﹣1)是“爱心点”,请判断点M在第几象限?并说明理由.
19.在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a级关联点”(其中a为常数,且a≠0),例如,点P(1,4)的“2级关联点”为Q(2×1+4,1+2×4),即Q(6,9).
(1)若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为
;
(2)若点P的“5级关联点”的坐标为(9,﹣3),求点P的坐标;
(3)若点P(m﹣1,2m)的“﹣3级关联点”P′位于坐标轴上.求点P′的坐标.
参考答案与试题解析
一.选择题
1.【解答】解:假设A1(1,2),则A2(1,﹣2),A3(﹣3,﹣2),A4(﹣3,2),A5(1,2),…,
∴A4n+1(1,2),A4n+2(1,﹣2),A4n+3(﹣3,﹣2),A4n+4(﹣3,2)(n为自然数).
∵2020=505×4,
∴A2020的坐标为(﹣3,2),
∴A2021(1,2),A1(1,2),
∴x+y=3.
故选:C.
2.【解答】解:∵点P(a﹣5,a+1)在y轴上,
∴a﹣5=0,
解得:a=5.
故选:D.
3.【解答】解:∵点P(x,y)在第二象限,且|x|=5,|y|=2,
∴x=﹣5,y=2,
∴点P的坐标为(﹣5,2).
故选:A.
4.【解答】解:∵点P(m,n)在第三象限,
∴m<0,n<0,
∴﹣m>0,|n|>0,
∴点Q(﹣m,|n|)在第一象限.
故选:A.
5.【解答】解:A、(2,0)在x轴上,不合题意;
B、(﹣2,3)在第二象限,不合题意;
C、(﹣3,﹣5)在第三象限,不合题意;
D、(2,﹣5),在第四象限,符合题意.
故选:D.
6.【解答】解:∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2025÷10=202…5,
∴细线另一端在绕四边形第203圈的第5个单位长度的位置,
即细线另一端所在位置的点的坐标是(﹣1,﹣2).
故选:D.
7.【解答】解:观察发现,第2次跳动至点的坐标是(2,1),
第4次跳动至点的坐标是(3,2),
第6次跳动至点的坐标是(4,3),
第8次跳动至点的坐标是(5,4),
…
第2n次跳动至点的坐标是(n+1,n),
∴第124次跳动至点的坐标是(63,62).
故选:A.
8.【解答】解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…
右下角的点的横坐标为n时,共有n2个,
∵452=2025,45是奇数,
∴第2025个点是(45,0),
第2020个点是(45,5).
故选:D.
9.【解答】解:如图,根据题意得:P0(0,3),P1(3,0),P2(7,4),P3(8,3),P4(5,0),P5(1,4),P6(0,3),P7(3,0),…,
∴点Pn的坐标6次一循环.经过6次反弹后动点回到出发点(0,3),
∵2020÷6=336…4,
∴当点P第2020次碰到矩形的边时为第336个循环组的第4次反弹,
点P的坐标为(5,0).
故选:A.
10.【解答】解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4,(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),
∵2019=504×4+3,
∴A2019(505,505).
故选:A.
二.填空题(共5小题)
11.【解答】解:∵点A(2﹣m,3m﹣12)在x轴上,
∴3m﹣12=0,
解得:m=4,
故答案为:4.
12.【解答】解:由题意,得
x=5或x=﹣5,y=﹣6,
即点的坐标为:(﹣5,﹣6)或(5,﹣6),
故答案为:(﹣5,﹣6)或(5,﹣6).
13.【解答】解:点(﹣5,1)到y轴的距离等于:|﹣5|=5.
故答案为:5.
14.【解答】解:如图所示:点A的坐标是(1,﹣2).
故答案为:(1,﹣2).
15.【解答】解:(1)观察各点规律发现:
第1、4、7、10个点在x轴上,偶数是负号,奇数是正号,
坐标分别(1,0),(﹣2,0),(3,0),(﹣4,0),…,
第2、5、8个点在y轴上,偶数是负号,奇数是正号,
坐标分别(0,1),(0,﹣2),(0,3),…,
第3、6、9个点在一三象限,
坐标分别(1,1),(﹣2,﹣2),(3,3),…,
∵1000÷3=333余1,
∴第1000个点在x轴负半轴上,坐标为(﹣334,0).
故答案为:(﹣334,0).
三.解答题(共4小题)
16.【解答】解:(1)∵xy=0,
∴x=0或y=0或x=0且y=0,
∴点M在y轴或x轴或原点;
(2)∵>0,
∴横纵坐标同号,
∴点M在第一象限或第三象限.
17.【解答】解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=,
所以,当a=时,点M在x轴上;
(2)要使点M在第二象限,a应满足,解得,
所以,当时,点M在第二象限;
(3)要使点M到y轴距离是1,a应满足|a﹣1|=1,解得a=2或a=0,
所以,当a=2或a=0时,点M到y轴距离是1.
18.【解答】解:(1)当A(5,3)时,m﹣1=5,=3,
解得m=6,n=4,
则2m=12,8+n=12,
所以2m=8+n,
所以A(5,3)是“爱心点”;
当B(4,8)时,m﹣1=4,=8,
解得m=5,n=14,显然2m≠8+n,
所以B点不是“爱心点”;
(2)点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“爱心点”,
∴m﹣1=a,=2a﹣1,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1
2a﹣1=﹣3,
∴M(﹣1,﹣3)故点M在第三象限.
19.【解答】解:(1)3×(﹣1)+5=2;﹣1+3×5=14,
∴若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为(2,14).
故答案为:(2,14);
(2)设点P的坐标为(a,b),
由题意可知,
解得:,
∴点P的坐标为(2,﹣1);
(3)∵点P(m﹣1,2m)的“﹣3级关联点”为P′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),①P′位于x轴上,
∴m﹣1+(﹣3)×2m=0,
解得:m=,
∴﹣3(m﹣1)+2m=,
∴P′(,0).
②P′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴P′(0,﹣16).
综上所述,点P′的坐标为(,0)或(0,﹣16).
