15.2.2完全平公式
图片预览

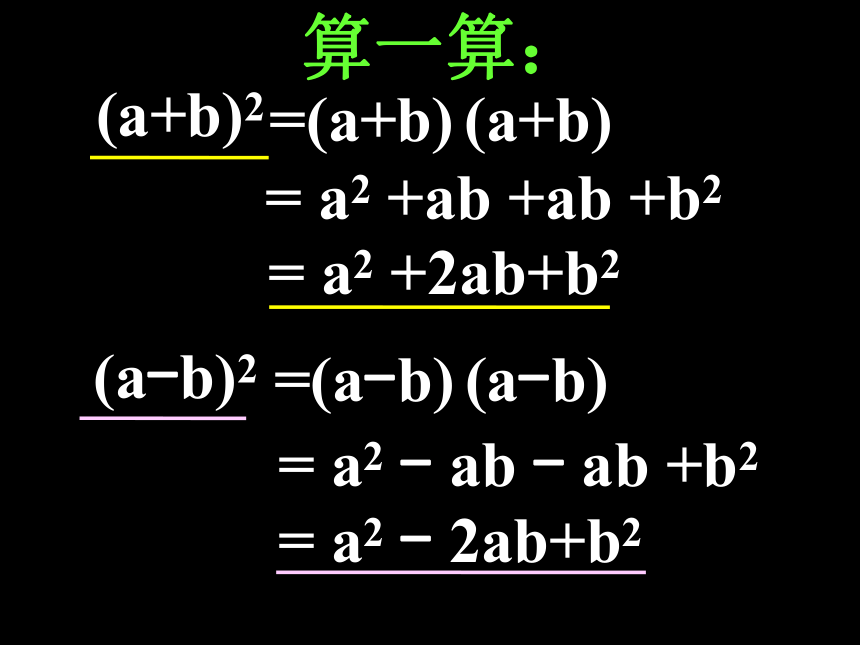




文档简介
(共26张PPT)
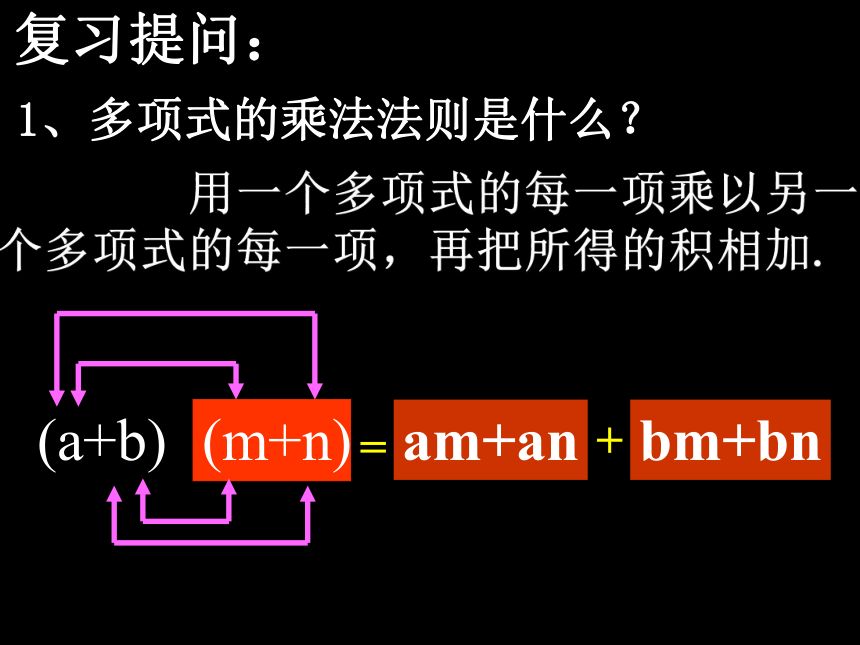
复习提问:
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
1、多项式的乘法法则是什么?
am+an
bm+bn
+
=
(m+n)
(a+b)
算一算:
(a+b)2
(a-b)2
= a2 +2ab+b2
= a2 - 2ab+b2
= a2 +ab +ab +b2
= a2 - ab - ab +b2
=(a+b) (a+b)
=(a-b) (a-b)
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
b
b
a
a
(a+b)
a
b
ab
ab
+
+
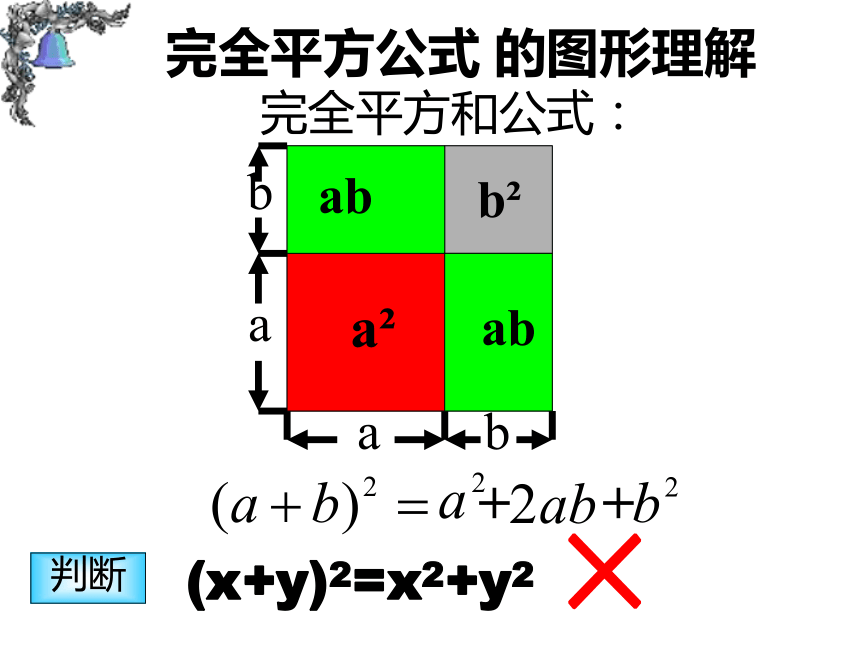
完全平方和公式:
完全平方公式 的图形理解
判断
(x+y)2=x2+y2
×
a
a
b
b
(a-b)
a
ab
ab
b
b
b
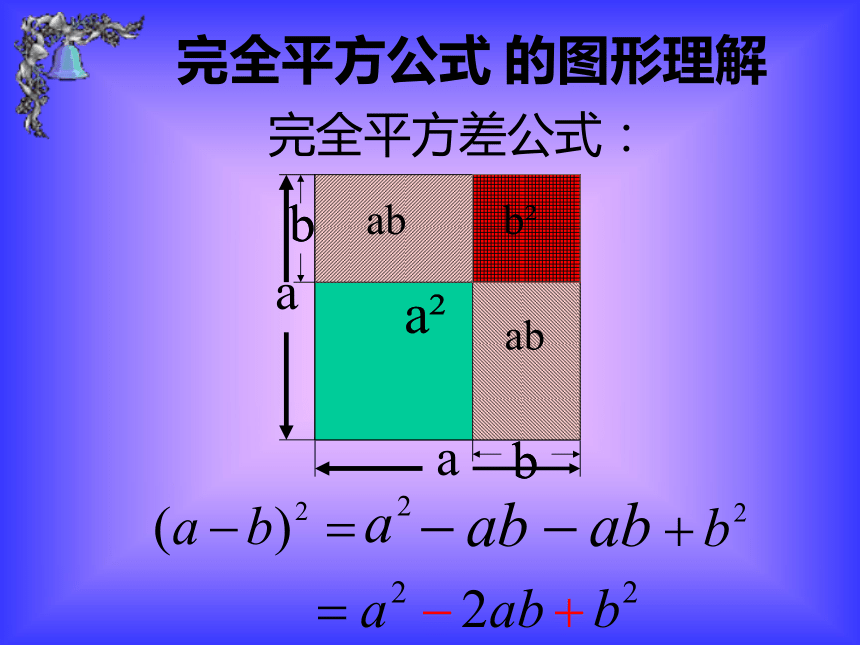
完全平方差公式:
完全平方公式 的图形理解
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方,末平方,首末两倍中间放
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
例1 运用完全平方公式计算:
解: (x+2y)2=
=x2
(1)(x+2y)2
(a +b)2= a2 + 2 ab + b2
x2
+2 x 2y
+(2y)2
+4xy
+4y2
例1 运用完全平方公式计算:
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
例2、运用完全平方公式计算:
(1) ( 4a2 - b2 )2
分析:
4a2
a
b2
b
解:
( 4a2 - b2)2
=( )2-2( )·( )+( )2
=16a4-8a2b2+b4
记清公式、代准数式、准确计算。
解题过程分3步:
(a-b)2= a2 - 2ab+b2
4a2
4a2
b2
b2
= x2 – 2xy2+4y4
(2) ( x – 2y2)2
+(2y2)2
解:( x – 2y2)2 =
(a - b)2 = a2 - 2ab + b2
( x)2
– 2 ( x) (2y2)
1.(3x-7y)2=
2.(2a2+3b)2=
算一算
运用完全平方公式计算:
(1) 1042
解: 1042
= (100+4)2
=10000+800+16
=10816
(2) 99.992
解: 99.992
= (100 –0.01)2
=10000 -2+0.0001
=9998.0001
1992
8.92
利用完全平方公式计算:
例3 计算:
(1) ( a2 + b3)2
(2)(- x2y - )2
1.(-x-y)2=
2.(-2a2+b)2=
你会了吗
通过这节课的学习你学到了什么
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及
其指数;
几点注意:
1、项数:积的项数为三;
2、符号:特别是(a-b)2= a2 - 2ab+b2;
3、字母:不要漏写;
4、字母指数:当公式中的a、b所代表的
单项式字母指数不是1时,乘方时要
记住字母指数需乘2。
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、公式的逆向使用;
4、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2
(2) (a - b)2 、 (b - a)2 、
(-b +a)2 与(-a +b)2
(1) (-a -b)2 与(a+b)2
2、比较下列各式之间的关系:
相等
相等
(1) (6a+5b)2
(2) (4x-3y)2
(3) (2m-1)2
(3) (-2m-1)2
3、填空:
x2+2xy+y2=( )2
x+y
x2+2x+1=( )2
x+1
a2-4ab+4b2=( )2
a-2b
x2-4x +4=( )2
x-2
注意:
公式的逆用,
公式中各项
符号及系数。
a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2
3、公式的逆向使用;
代数式2xy-x2-y2= ( )
A.(x-y)2 B.(-x-y)2 C.(y-x)2 D.-(x-y)2
选择
D
复习提问:
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
1、多项式的乘法法则是什么?
am+an
bm+bn
+
=
(m+n)
(a+b)
算一算:
(a+b)2
(a-b)2
= a2 +2ab+b2
= a2 - 2ab+b2
= a2 +ab +ab +b2
= a2 - ab - ab +b2
=(a+b) (a+b)
=(a-b) (a-b)
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式:
完全平方公式 的图形理解
判断
(x+y)2=x2+y2
×
a
a
b
b
(a-b)
a
ab
ab
b
b
b
完全平方差公式:
完全平方公式 的图形理解
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方,末平方,首末两倍中间放
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
例1 运用完全平方公式计算:
解: (x+2y)2=
=x2
(1)(x+2y)2
(a +b)2= a2 + 2 ab + b2
x2
+2 x 2y
+(2y)2
+4xy
+4y2
例1 运用完全平方公式计算:
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
例2、运用完全平方公式计算:
(1) ( 4a2 - b2 )2
分析:
4a2
a
b2
b
解:
( 4a2 - b2)2
=( )2-2( )·( )+( )2
=16a4-8a2b2+b4
记清公式、代准数式、准确计算。
解题过程分3步:
(a-b)2= a2 - 2ab+b2
4a2
4a2
b2
b2
= x2 – 2xy2+4y4
(2) ( x – 2y2)2
+(2y2)2
解:( x – 2y2)2 =
(a - b)2 = a2 - 2ab + b2
( x)2
– 2 ( x) (2y2)
1.(3x-7y)2=
2.(2a2+3b)2=
算一算
运用完全平方公式计算:
(1) 1042
解: 1042
= (100+4)2
=10000+800+16
=10816
(2) 99.992
解: 99.992
= (100 –0.01)2
=10000 -2+0.0001
=9998.0001
1992
8.92
利用完全平方公式计算:
例3 计算:
(1) ( a2 + b3)2
(2)(- x2y - )2
1.(-x-y)2=
2.(-2a2+b)2=
你会了吗
通过这节课的学习你学到了什么
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及
其指数;
几点注意:
1、项数:积的项数为三;
2、符号:特别是(a-b)2= a2 - 2ab+b2;
3、字母:不要漏写;
4、字母指数:当公式中的a、b所代表的
单项式字母指数不是1时,乘方时要
记住字母指数需乘2。
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、公式的逆向使用;
4、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2
(2) (a - b)2 、 (b - a)2 、
(-b +a)2 与(-a +b)2
(1) (-a -b)2 与(a+b)2
2、比较下列各式之间的关系:
相等
相等
(1) (6a+5b)2
(2) (4x-3y)2
(3) (2m-1)2
(3) (-2m-1)2
3、填空:
x2+2xy+y2=( )2
x+y
x2+2x+1=( )2
x+1
a2-4ab+4b2=( )2
a-2b
x2-4x +4=( )2
x-2
注意:
公式的逆用,
公式中各项
符号及系数。
a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2
3、公式的逆向使用;
代数式2xy-x2-y2= ( )
A.(x-y)2 B.(-x-y)2 C.(y-x)2 D.-(x-y)2
选择
D
