沪教版(上海)数学七年级第二学期-14.5 等腰三角形的性质 教案
文档属性
| 名称 | 沪教版(上海)数学七年级第二学期-14.5 等腰三角形的性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 171.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 00:00:00 | ||
图片预览

文档简介
§14.5等腰三角形的性质
教学目标:
通过观察、动手操作后猜想等腰三角形的性质,再归纳出等腰三角形两个底角相等的性质。
经历用说理的方法推导等腰三角形两个底角相等的这个性质的过程
掌握等腰三角形两个底角相等及等腰三角形的“三线合一”的性质,能运用等腰三角形的性质解决有关的简单问题,培养基础的逻辑推理能力.
教学重点:等腰三角形的性质的探究说理及应用.
教学难点:等腰三角形“三线合一”性质的说理和简单运用。
教学过程:
教师活动
学生活动
设计意图
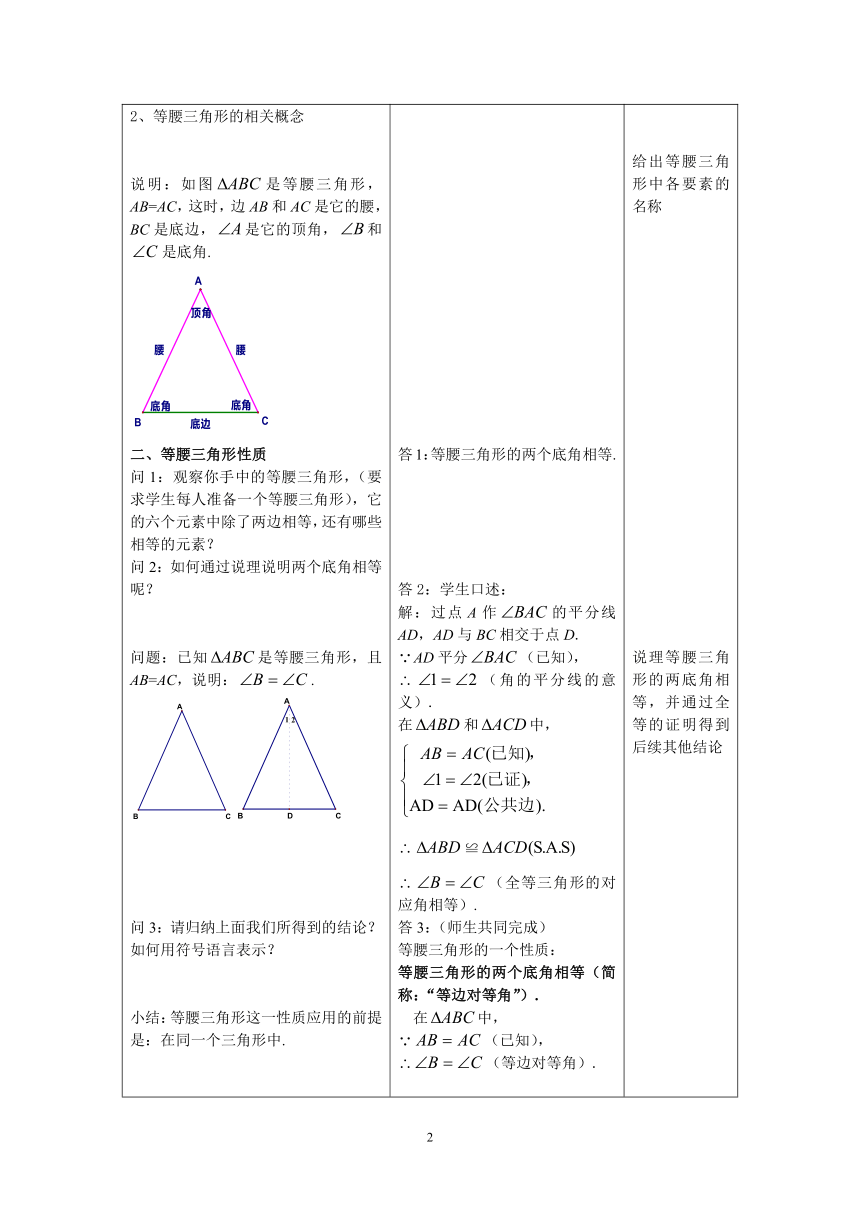
等腰三角形的相关概念
1、引入:
问1:能否把两个全等的直角三角形拼成一个三角形?
2、老师说理:
将边AC放到A1C1上,因为AC=A1C1,所以线段AC与线段A1C1重合,
因为==90°,所以+=180°,所以点B、C、C1、B1共线。可见我们成功的把两个三角形拼成了一个三角形。
问2:得到的三角形边有什么特点?
问3:有两条边相等的三角形叫作什么三角形?
出示课题:§14.5等腰三角形的性质
2、等腰三角形的相关概念
说明:如图是等腰三角形,AB=AC,这时,边AB和AC是它的腰,BC是底边,是它的顶角,和是底角.
二、等腰三角形性质
问1:观察你手中的等腰三角形,(要求学生每人准备一个等腰三角形),它的六个元素中除了两边相等,还有哪些相等的元素?
问2:如何通过说理说明两个底角相等呢?
问题:已知是等腰三角形,且AB=AC,说明:.
问3:请归纳上面我们所得到的结论?如何用符号语言表示?
小结:等腰三角形这一性质应用的前提是:在同一个三角形中.
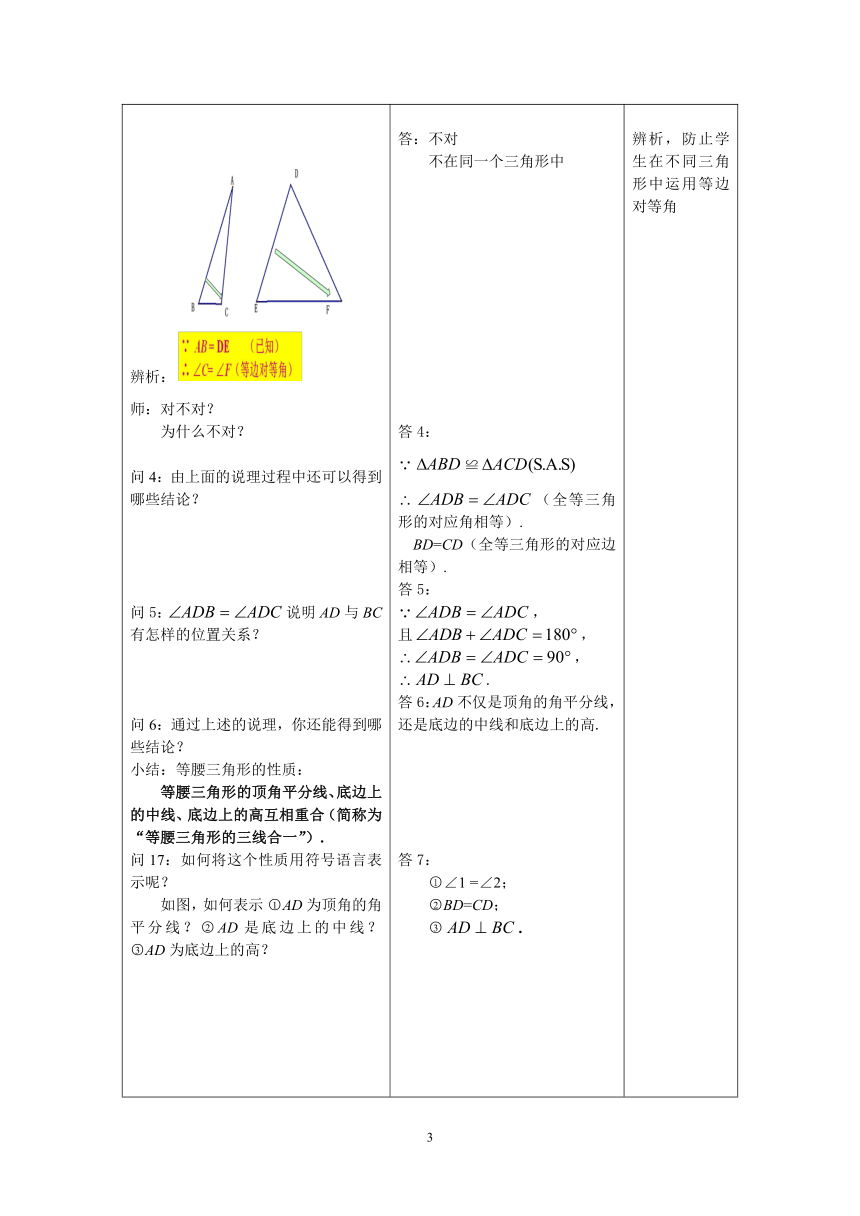
辨析:
师:对不对?
为什么不对?
问4:由上面的说理过程中还可以得到哪些结论?
问5:说明AD与BC有怎样的位置关系?
问6:通过上述的说理,你还能得到哪些结论?
小结:等腰三角形的性质:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”).
问17:如何将这个性质用符号语言表示呢?
如图,如何表示AD为顶角的角平分线?AD是底边上的中线?AD为底边上的高?
说明:“等腰三角形的三线合一”这一性质指的是以上、、中已知其中任意一个就可以得出其余两个.
问8:请用符号语言表是:
由得、
由得、
由得、
问913:通过上述的说理,你还能得到哪些结论?
问10:对称轴是什么?
三、等腰三角形性质的应用
我们通过探究得到了等腰三角形的三个重要性质,它们如何应用呢?
试一试:
(1)如图,已知AB=AC,,求和的度数.
问1:题中有哪些条件?求什么?
问2:如何求?依据是什么?
教师根据学生回答板书:
解:(1)∵
(已知),
∴(等边对等角),
∵(已知),
∴(等量代换).
(2)∵,
又(三角形内角和等于),
∴.
小结:在等腰三角形中若已知一个内角,即可求出其它内角的大小.
小结:分类讨论的数学思想
(3)如图,已知AB=AC,,AD是的中线,则=_______,=________;
问:如何思考?
小结:若已知等腰三角形及顶角平分线、底边中线、底边上的高三线之一,可考虑用“等腰三角形三线合一”的性质来说明,而不用三角形的全等,以简化说理过程.
课堂练习:P107,2、3.
五、课堂小结
今天你主要学习了什么,有什么收获?
六、布置作业
练习册,习题14.5
答1:能
演示拼的过程和成果
答2:有两条边相等
答3:有两边相等的三角形叫做等腰三角形.
答1:等腰三角形的两个底角相等.
答2:学生口述:
解:过点A作的平分线AD,AD与BC相交于点D.
AD平分(已知),
(角的平分线的意义).
在和中,
≌
(全等三角形的对应角相等).
答3:(师生共同完成)
等腰三角形的一个性质:
等腰三角形的两个底角相等(简称:“等边对等角”).
在中,
(已知),
(等边对等角).
答:不对
不在同一个三角形中
答4:
≌
(全等三角形的对应角相等).
BD=CD(全等三角形的对应边相等).
答5:
,
且,
,
.
答6:AD不仅是顶角的角平分线,还是底边的中线和底边上的高.
答7:
∠1
=∠2;
BD=CD;
.
答8:(师生共同完成)
(1)已知等腰三角形的顶角平分线:
在三角形ABC中,AB=AC
,
∵
AD是角平分线
(已知),
∴
,BD=
CD(等腰三角形的三线合一).
(2)已知等腰三角形底边上的中线:
在三角形ABC中,AB=AC,
∵AD是中线(已知)
∴
AD⊥BC
,
∠1
=∠2(等腰三角形的三线合一)
(3)已知等腰三角形底边上的高:
在三角形ABC中,AB=AC,
∵AD是高(已知)
∴
BD=CD,
∠1
=∠2(等腰三角形的三线合一)
答9:等腰三角形是轴对称图形
答10:等腰三角形的对称轴还可认为是底边上的高所在的直线,或底边上的中线所在的直线.
答1:题中已知等腰三角形的底角,求其另一底角和顶角的度数.
答2:由等腰三角形“等边对等角”的性质、三角形内角和性质求解.
生答:
预设1,利用已知条件说明和全等,从而得出所求结论.
预设2,
本题已知等腰三角形顶角,及底边上的中线,可考虑用“等腰三角形三线合一”的性质求解.
∵
(已知),
又∵AD是的中线(已知)
∴(等腰三角形三线合一),
∵(已知),
∴(等式性质).
通过操作引出等腰三角形,同时给学生一个等腰三角形的对称性的印象。
给出等腰三角形中各要素的名称
说理等腰三角形的两底角相等,并通过全等的证明得到后续其他结论
辨析,防止学生在不同三角形中运用等边对等角
培养学生将文字语言转化成符号语言的能力
6
教学目标:
通过观察、动手操作后猜想等腰三角形的性质,再归纳出等腰三角形两个底角相等的性质。
经历用说理的方法推导等腰三角形两个底角相等的这个性质的过程
掌握等腰三角形两个底角相等及等腰三角形的“三线合一”的性质,能运用等腰三角形的性质解决有关的简单问题,培养基础的逻辑推理能力.
教学重点:等腰三角形的性质的探究说理及应用.
教学难点:等腰三角形“三线合一”性质的说理和简单运用。
教学过程:
教师活动
学生活动
设计意图
等腰三角形的相关概念
1、引入:
问1:能否把两个全等的直角三角形拼成一个三角形?
2、老师说理:
将边AC放到A1C1上,因为AC=A1C1,所以线段AC与线段A1C1重合,
因为==90°,所以+=180°,所以点B、C、C1、B1共线。可见我们成功的把两个三角形拼成了一个三角形。
问2:得到的三角形边有什么特点?
问3:有两条边相等的三角形叫作什么三角形?
出示课题:§14.5等腰三角形的性质
2、等腰三角形的相关概念
说明:如图是等腰三角形,AB=AC,这时,边AB和AC是它的腰,BC是底边,是它的顶角,和是底角.
二、等腰三角形性质
问1:观察你手中的等腰三角形,(要求学生每人准备一个等腰三角形),它的六个元素中除了两边相等,还有哪些相等的元素?
问2:如何通过说理说明两个底角相等呢?
问题:已知是等腰三角形,且AB=AC,说明:.
问3:请归纳上面我们所得到的结论?如何用符号语言表示?
小结:等腰三角形这一性质应用的前提是:在同一个三角形中.
辨析:
师:对不对?
为什么不对?
问4:由上面的说理过程中还可以得到哪些结论?
问5:说明AD与BC有怎样的位置关系?
问6:通过上述的说理,你还能得到哪些结论?
小结:等腰三角形的性质:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”).
问17:如何将这个性质用符号语言表示呢?
如图,如何表示AD为顶角的角平分线?AD是底边上的中线?AD为底边上的高?
说明:“等腰三角形的三线合一”这一性质指的是以上、、中已知其中任意一个就可以得出其余两个.
问8:请用符号语言表是:
由得、
由得、
由得、
问913:通过上述的说理,你还能得到哪些结论?
问10:对称轴是什么?
三、等腰三角形性质的应用
我们通过探究得到了等腰三角形的三个重要性质,它们如何应用呢?
试一试:
(1)如图,已知AB=AC,,求和的度数.
问1:题中有哪些条件?求什么?
问2:如何求?依据是什么?
教师根据学生回答板书:
解:(1)∵
(已知),
∴(等边对等角),
∵(已知),
∴(等量代换).
(2)∵,
又(三角形内角和等于),
∴.
小结:在等腰三角形中若已知一个内角,即可求出其它内角的大小.
小结:分类讨论的数学思想
(3)如图,已知AB=AC,,AD是的中线,则=_______,=________;
问:如何思考?
小结:若已知等腰三角形及顶角平分线、底边中线、底边上的高三线之一,可考虑用“等腰三角形三线合一”的性质来说明,而不用三角形的全等,以简化说理过程.
课堂练习:P107,2、3.
五、课堂小结
今天你主要学习了什么,有什么收获?
六、布置作业
练习册,习题14.5
答1:能
演示拼的过程和成果
答2:有两条边相等
答3:有两边相等的三角形叫做等腰三角形.
答1:等腰三角形的两个底角相等.
答2:学生口述:
解:过点A作的平分线AD,AD与BC相交于点D.
AD平分(已知),
(角的平分线的意义).
在和中,
≌
(全等三角形的对应角相等).
答3:(师生共同完成)
等腰三角形的一个性质:
等腰三角形的两个底角相等(简称:“等边对等角”).
在中,
(已知),
(等边对等角).
答:不对
不在同一个三角形中
答4:
≌
(全等三角形的对应角相等).
BD=CD(全等三角形的对应边相等).
答5:
,
且,
,
.
答6:AD不仅是顶角的角平分线,还是底边的中线和底边上的高.
答7:
∠1
=∠2;
BD=CD;
.
答8:(师生共同完成)
(1)已知等腰三角形的顶角平分线:
在三角形ABC中,AB=AC
,
∵
AD是角平分线
(已知),
∴
,BD=
CD(等腰三角形的三线合一).
(2)已知等腰三角形底边上的中线:
在三角形ABC中,AB=AC,
∵AD是中线(已知)
∴
AD⊥BC
,
∠1
=∠2(等腰三角形的三线合一)
(3)已知等腰三角形底边上的高:
在三角形ABC中,AB=AC,
∵AD是高(已知)
∴
BD=CD,
∠1
=∠2(等腰三角形的三线合一)
答9:等腰三角形是轴对称图形
答10:等腰三角形的对称轴还可认为是底边上的高所在的直线,或底边上的中线所在的直线.
答1:题中已知等腰三角形的底角,求其另一底角和顶角的度数.
答2:由等腰三角形“等边对等角”的性质、三角形内角和性质求解.
生答:
预设1,利用已知条件说明和全等,从而得出所求结论.
预设2,
本题已知等腰三角形顶角,及底边上的中线,可考虑用“等腰三角形三线合一”的性质求解.
∵
(已知),
又∵AD是的中线(已知)
∴(等腰三角形三线合一),
∵(已知),
∴(等式性质).
通过操作引出等腰三角形,同时给学生一个等腰三角形的对称性的印象。
给出等腰三角形中各要素的名称
说理等腰三角形的两底角相等,并通过全等的证明得到后续其他结论
辨析,防止学生在不同三角形中运用等边对等角
培养学生将文字语言转化成符号语言的能力
6
