直线.线段.射线正式导学案
文档属性
| 名称 | 直线.线段.射线正式导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 25.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 15:57:19 | ||
图片预览


文档简介
4.2 线段、射线和直线导学案 (1)
知识回顾
几何图形是由 、 、 、 组成的. 点动成 ,线动成 ,面动成 . 是组成图形的基本元素.
学习目标
1、知识技能:①理解两点确定一条直线的事实.
②掌握直线、射线、线段的表示方法.
③理解直线、射线、线段的联系和区别.
2﹑数学思考:①通过学习直线、射线、线段的表示方法,使学生建立初步的符号感.
②通过学习直线、射线、线段的联系和区别,进一步发展学生抽象概括的能力.
3、解决问题:通过对直线射线性质的研究,体会它们在解决实际问题中的作用,并能用它们解释生活中的一些现象.
4、情感态度:①通过分组,培养学生合作交流的意识和探索精神.
②通过对直线的性质的探究,使学生初步认识到数学与现实生活的密切联系,感受数学的严谨性以及数学结论的确定性.
学习重点:两点确定一条直线.
学习难点:不同几何语言的相互转化.
一、学案自学
(一)线段、射线和直线的概念
自学要求:请自主学习课本的内容,要求解决两个问题:
1.线段、射线和直线的概念是什么?
2.在我们的现实生活中,还有那些物体可以近似看做线段、射线和直线?
对应训练一:
1.绷紧的琴弦、人行横道线都可以近似地看做 .线段有 端点.
2.将线段向一个方向无限延伸就形成了 .射线有 个端点.
3.将线段向两个方向无限延伸就形成了 .直线 端点.
(二)图形的表示方法
自学要求:请自主学习课本的内容,试着理解线段、射线和直线的表示方法.
对应训练二:
1.如何表示不同的线段呢?
(1)用表示两个端点的大写字母表示:图1中的线段记为 (或 ),图2中的线段记为 (或 ).
(2)用一个小写字母表示:图1中的线段记为 、图2中的线段记为 .
2.如何表示射线呢?
射线 (注意:不能记为射线 )
3.直线又该怎样表示?
直线 (或 )
4.连一连,请你把左边对图形的描述和右边相应的图形用线连起来.
以A为端点,经过点B的射线
连结A,B两点的线段
经过A,B两点的直线
(三)两点确定一条直线
自学要求:请认真看课本的内容,要求解决三个问题:1、一个点与一条直线有几种位置关系?2、两点确定一条直线的含义.3、什么是两条直线相交?
对应训练三:
1.在一条笔直的校园大道两旁种树时,先定下两棵树的位置,然后其他树的位置就
容易确定下来,这说明了什么?
2.建筑工人在工地上的两个木楔上栓上一根细线,这样可以保证建起的墙是直的,请说明理由.
3.经过一张纸上的三个点中每两个点画直线,最少可以画多少条?最多可以画多少条?
二、小组合作
1.如图(1),用两种方式分别表示图中的两条直线.
⑴ ⑵
2.如图(2),已知点O、P、Q,画线段PQ,射线OP和直线OQ.
三、班级展示
四、质疑探究
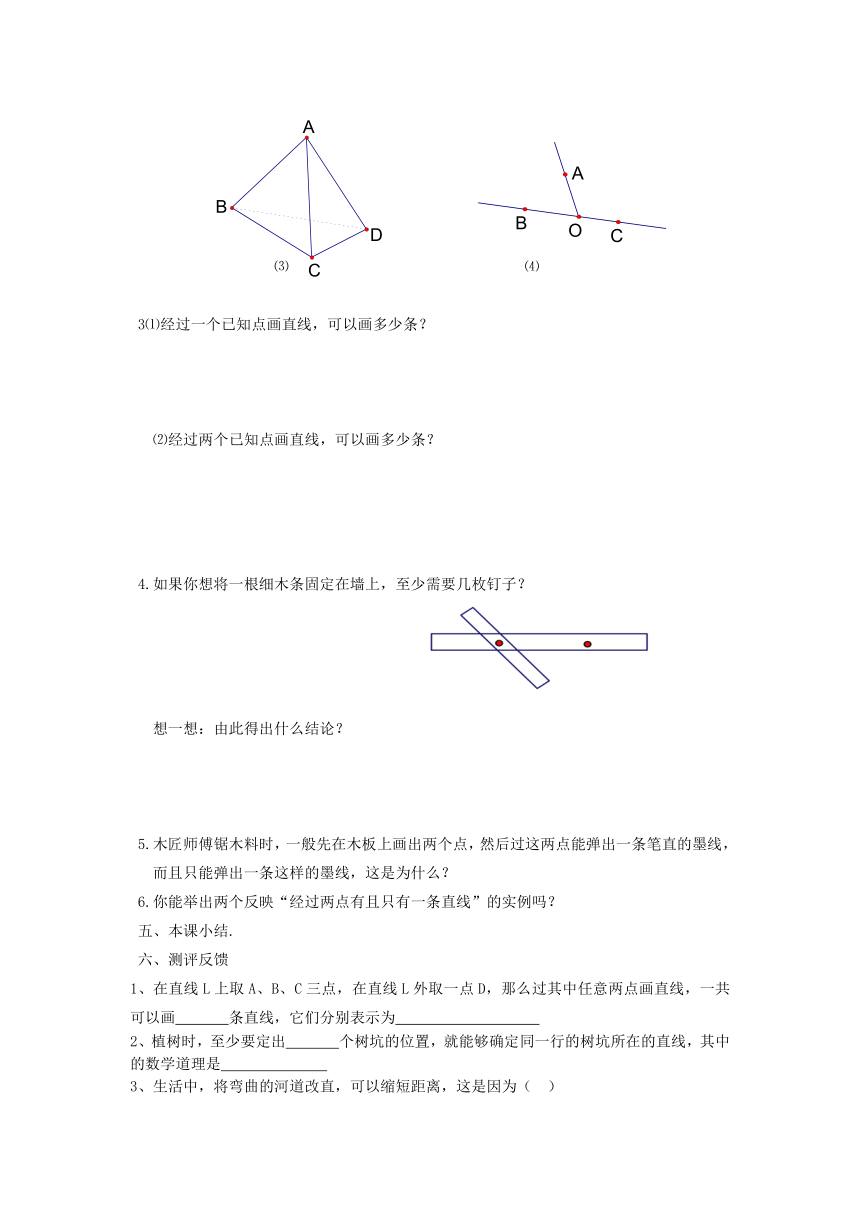
1.图(3)中的几何体有多少条棱?请写出这些表示棱的线段.
2.请写出图(4)中以点O为端点的所有射线.
⑶ ⑷
3⑴经过一个已知点画直线,可以画多少条?
⑵经过两个已知点画直线,可以画多少条?
4.如果你想将一根细木条固定在墙上,至少需要几枚钉子?
想一想:由此得出什么结论?
5.木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点能弹出一条笔直的墨线,而且只能弹出一条这样的墨线,这是为什么?
6.你能举出两个反映“经过两点有且只有一条直线”的实例吗?
五、本课小结.
六、测评反馈
1、在直线L上取A、B、C三点,在直线L外取一点D,那么过其中任意两点画直线,一共可以画 条直线,它们分别表示为
2、植树时,至少要定出 个树坑的位置,就能够确定同一行的树坑所在的直线,其中的数学道理是
3、生活中,将弯曲的河道改直,可以缩短距离,这是因为( )
A、因为它是直线
B、两点确定一条直线
C、两点间距离的定义
D、两点之间,线段最短。
七、出示答案.
1. 4 线段AB,线段AD,线段BD,线段CD
2. 2 两点确定一条直线
3. D
八、验收本节课学生掌握的效果.
做的好的学生给予表扬,做的不好的学生给予鼓励.
九、布置作业.
习题4.2第2、3、4题
课题 4.2直线、射线、线段(2)
【学习目标】:1、会用尺规画一条线段等于已知线段;
2、会比较两条线段的长短;
3、理解线段中点的概念,了解“两点之间,线段最短”的性质。
【学习重点】:线段的中点概念,“两点之间,线段最短”的性质是重点;
【学习难点】:画一条线段等于已知线段是难点。
【导学指导】
一、温故知新
1、过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是对的。
二、自主学习
问题:现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:
已知线段a,画一条线段等于已知线段。
1.作一条线段等于已知线段
现在我们来解决这个问题。
作法:
(1)作射线AM
(2)在AM上截取AB= a。
则线段AB为所求。
应用:已知线段a、b,求作线段AB=a+b。
解:(1)作射线AM;
(2)在AM上顺次截取AC=a,CB= b。
则AB= a+b为所求。
做一做:作线段AB=a-b。
2、比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?
我们先来回答下面的问题。
怎样比较两个同学的身高?
一是用尺子测量;二是站在一起比(脚在同一高度)。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
(1)度量法:用刻度尺分别量出两条线段的长度从而进行比较。
( 2)把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。(如图)
AB<CD AB>CD AB=CD
3、线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点;
记作AM=MB或AM=MB=1/2AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的三等分点。类似地,还有四等分点,等等。
4、线段的性质
请同学们思考课本131页的思考?
结论:
两点所连的线中,
简单地说成:___________________________________
你能举出这条性质在生活中的一些应用吗?
两点间的距离的定义:___________________________________
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
【课堂练习】
1、课本131页练习1、2
2、在直线上顺次取A、B、C三点,使 AB=4㎝,BC=3㎝,点O是线段AC的中点,则线段OB的长是〔 〕
A、2㎝ B、1.5㎝ C、0.5㎝ D、3.5㎝
3、已知线段AB=5㎝,C是直线AB上一点,若BC=2㎝,则线段AC的长为
【要点归纳】:
1、画一条线段等于一条已知线段。
2、怎样比较两条线段的长短?
3、线段的性质是什么?
4、什么是两点间的距离?
【拓展训练】:
1、把弯曲的河道改直后,缩短了河道的长度,这是因为 ;
2、已知,如图,AB=16㎝,C是BC的中点,且AC=10㎝,D是AC的中点,E是BC的中点,求线段DE的长。
【总结反思】:
C
D
b
图2
A
B
a
图1
A
E
A
B
A
B
a
M
B
·
·
A
a
b
C
M
B
·
·
A
A(C)
B
(D)
A(C)
(D)
B
A(C)
B(D)
A
B
M
A
B
M
N
(1)
(2)
()
A
B
C
D
E
·
·
·
知识回顾
几何图形是由 、 、 、 组成的. 点动成 ,线动成 ,面动成 . 是组成图形的基本元素.
学习目标
1、知识技能:①理解两点确定一条直线的事实.
②掌握直线、射线、线段的表示方法.
③理解直线、射线、线段的联系和区别.
2﹑数学思考:①通过学习直线、射线、线段的表示方法,使学生建立初步的符号感.
②通过学习直线、射线、线段的联系和区别,进一步发展学生抽象概括的能力.
3、解决问题:通过对直线射线性质的研究,体会它们在解决实际问题中的作用,并能用它们解释生活中的一些现象.
4、情感态度:①通过分组,培养学生合作交流的意识和探索精神.
②通过对直线的性质的探究,使学生初步认识到数学与现实生活的密切联系,感受数学的严谨性以及数学结论的确定性.
学习重点:两点确定一条直线.
学习难点:不同几何语言的相互转化.
一、学案自学
(一)线段、射线和直线的概念
自学要求:请自主学习课本的内容,要求解决两个问题:
1.线段、射线和直线的概念是什么?
2.在我们的现实生活中,还有那些物体可以近似看做线段、射线和直线?
对应训练一:
1.绷紧的琴弦、人行横道线都可以近似地看做 .线段有 端点.
2.将线段向一个方向无限延伸就形成了 .射线有 个端点.
3.将线段向两个方向无限延伸就形成了 .直线 端点.
(二)图形的表示方法
自学要求:请自主学习课本的内容,试着理解线段、射线和直线的表示方法.
对应训练二:
1.如何表示不同的线段呢?
(1)用表示两个端点的大写字母表示:图1中的线段记为 (或 ),图2中的线段记为 (或 ).
(2)用一个小写字母表示:图1中的线段记为 、图2中的线段记为 .
2.如何表示射线呢?
射线 (注意:不能记为射线 )
3.直线又该怎样表示?
直线 (或 )
4.连一连,请你把左边对图形的描述和右边相应的图形用线连起来.
以A为端点,经过点B的射线
连结A,B两点的线段
经过A,B两点的直线
(三)两点确定一条直线
自学要求:请认真看课本的内容,要求解决三个问题:1、一个点与一条直线有几种位置关系?2、两点确定一条直线的含义.3、什么是两条直线相交?
对应训练三:
1.在一条笔直的校园大道两旁种树时,先定下两棵树的位置,然后其他树的位置就
容易确定下来,这说明了什么?
2.建筑工人在工地上的两个木楔上栓上一根细线,这样可以保证建起的墙是直的,请说明理由.
3.经过一张纸上的三个点中每两个点画直线,最少可以画多少条?最多可以画多少条?
二、小组合作
1.如图(1),用两种方式分别表示图中的两条直线.
⑴ ⑵
2.如图(2),已知点O、P、Q,画线段PQ,射线OP和直线OQ.
三、班级展示
四、质疑探究
1.图(3)中的几何体有多少条棱?请写出这些表示棱的线段.
2.请写出图(4)中以点O为端点的所有射线.
⑶ ⑷
3⑴经过一个已知点画直线,可以画多少条?
⑵经过两个已知点画直线,可以画多少条?
4.如果你想将一根细木条固定在墙上,至少需要几枚钉子?
想一想:由此得出什么结论?
5.木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点能弹出一条笔直的墨线,而且只能弹出一条这样的墨线,这是为什么?
6.你能举出两个反映“经过两点有且只有一条直线”的实例吗?
五、本课小结.
六、测评反馈
1、在直线L上取A、B、C三点,在直线L外取一点D,那么过其中任意两点画直线,一共可以画 条直线,它们分别表示为
2、植树时,至少要定出 个树坑的位置,就能够确定同一行的树坑所在的直线,其中的数学道理是
3、生活中,将弯曲的河道改直,可以缩短距离,这是因为( )
A、因为它是直线
B、两点确定一条直线
C、两点间距离的定义
D、两点之间,线段最短。
七、出示答案.
1. 4 线段AB,线段AD,线段BD,线段CD
2. 2 两点确定一条直线
3. D
八、验收本节课学生掌握的效果.
做的好的学生给予表扬,做的不好的学生给予鼓励.
九、布置作业.
习题4.2第2、3、4题
课题 4.2直线、射线、线段(2)
【学习目标】:1、会用尺规画一条线段等于已知线段;
2、会比较两条线段的长短;
3、理解线段中点的概念,了解“两点之间,线段最短”的性质。
【学习重点】:线段的中点概念,“两点之间,线段最短”的性质是重点;
【学习难点】:画一条线段等于已知线段是难点。
【导学指导】
一、温故知新
1、过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是对的。
二、自主学习
问题:现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:
已知线段a,画一条线段等于已知线段。
1.作一条线段等于已知线段
现在我们来解决这个问题。
作法:
(1)作射线AM
(2)在AM上截取AB= a。
则线段AB为所求。
应用:已知线段a、b,求作线段AB=a+b。
解:(1)作射线AM;
(2)在AM上顺次截取AC=a,CB= b。
则AB= a+b为所求。
做一做:作线段AB=a-b。
2、比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?
我们先来回答下面的问题。
怎样比较两个同学的身高?
一是用尺子测量;二是站在一起比(脚在同一高度)。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
(1)度量法:用刻度尺分别量出两条线段的长度从而进行比较。
( 2)把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。(如图)
AB<CD AB>CD AB=CD
3、线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点;
记作AM=MB或AM=MB=1/2AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的三等分点。类似地,还有四等分点,等等。
4、线段的性质
请同学们思考课本131页的思考?
结论:
两点所连的线中,
简单地说成:___________________________________
你能举出这条性质在生活中的一些应用吗?
两点间的距离的定义:___________________________________
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
【课堂练习】
1、课本131页练习1、2
2、在直线上顺次取A、B、C三点,使 AB=4㎝,BC=3㎝,点O是线段AC的中点,则线段OB的长是〔 〕
A、2㎝ B、1.5㎝ C、0.5㎝ D、3.5㎝
3、已知线段AB=5㎝,C是直线AB上一点,若BC=2㎝,则线段AC的长为
【要点归纳】:
1、画一条线段等于一条已知线段。
2、怎样比较两条线段的长短?
3、线段的性质是什么?
4、什么是两点间的距离?
【拓展训练】:
1、把弯曲的河道改直后,缩短了河道的长度,这是因为 ;
2、已知,如图,AB=16㎝,C是BC的中点,且AC=10㎝,D是AC的中点,E是BC的中点,求线段DE的长。
【总结反思】:
C
D
b
图2
A
B
a
图1
A
E
A
B
A
B
a
M
B
·
·
A
a
b
C
M
B
·
·
A
A(C)
B
(D)
A(C)
(D)
B
A(C)
B(D)
A
B
M
A
B
M
N
(1)
(2)
()
A
B
C
D
E
·
·
·
