17.2 勾股定理的逆定理 课件(共22张PPT)
文档属性
| 名称 | 17.2 勾股定理的逆定理 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 08:48:06 | ||
图片预览






文档简介
17.2 勾股定理的逆定理
2.会利用勾股定理的逆定理,判定直角三角形.
1.了解勾股定理的逆定理,并理解其证明方法.
3.理解原命题、逆命题、逆定理的概念及关系.
1.画图:画出边长分别是下列各组数的三角形(单位:厘米).
A:3、4、3 ;B:3、4、5;C:3、4、6;D:6、8、10
2.测量:用你的量角器分别测量一下上述各三角形的最大角的度数,并记录如下:A:____ B:____ C:____ D:____
3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______ C:______ D______
4.找规律:根据上述每个三角形所给的各组边长请你找出最长边的平方与其他两边的平方和之间的关系.
A:_____ B:_____ C:_____ D:______
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
你的猜想是_____________.
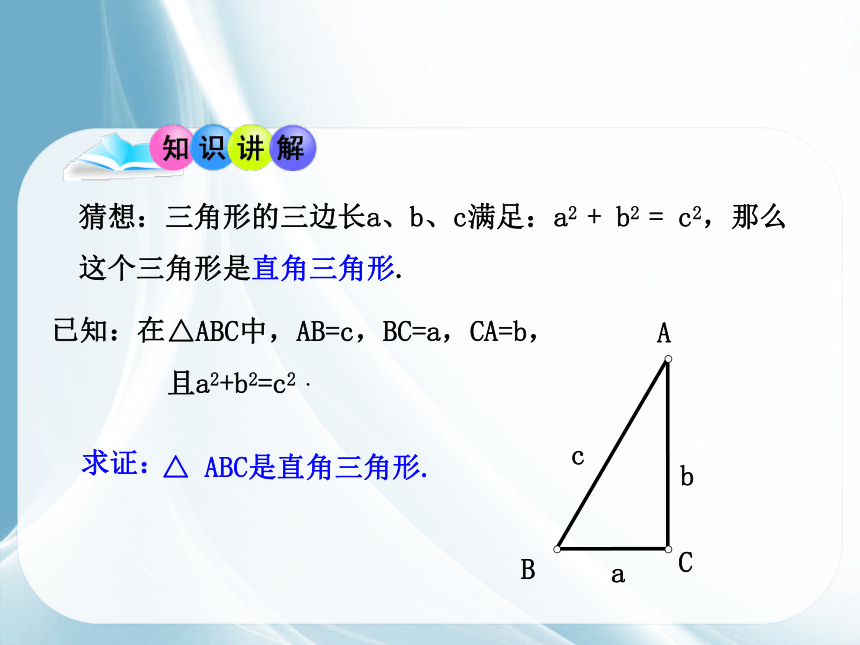
猜想:三角形的三边长a、b、c满足:a2 + b2 = c2,那么这个三角形是直角三角形.
已知:在
c
a
b
B
C
A
△ABC中,AB=c,BC=a,CA=b,
且a2+b2=c2 .
求证:
△ ABC是直角三角形.
已知:在△ABC中,AB=c,BC=a,CA=b,并且
证明:作?
在△ABC和△
∴?ABC
∠C=∠
a
b
(如图)求证:∠C=90°.
使∠
则有
中,
△
=90°.
≌
=90°,
A
B
b
c
C
a
B C a, C A b,
1 1 1 1
= =
A B a b ,BC B C , CA C A ,
2 2 2
1 1 1 1 1 1
= + = =
+ =
A B c, AB A B .
\ = \ =
a b c ,
2 2 2
1 1 1 1
Q
BC B C ,
CA C A ,
AB A B ,
1 1
1 1
1 1
=
=
=
定理:如果三角形的三边长a,b,c满足a2 + b2 = c2,那么这个三角形是直角三角形.
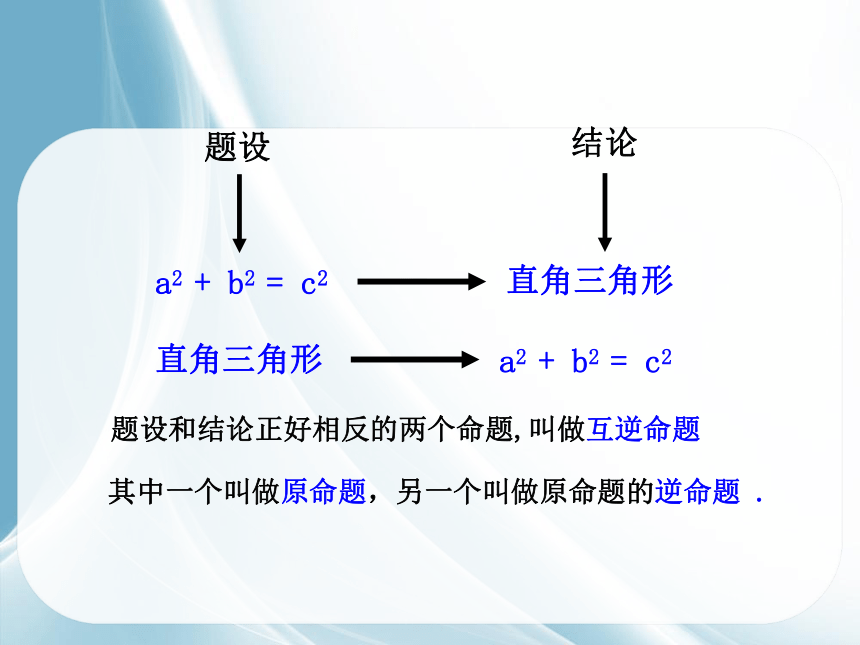
a2 + b2 = c2
题设
结论
直角三角形
直角三角形
a2 + b2 = c2
题设和结论正好相反的两个命题,叫做互逆命题
其中一个叫做原命题,另一个叫做原命题的逆命题 .
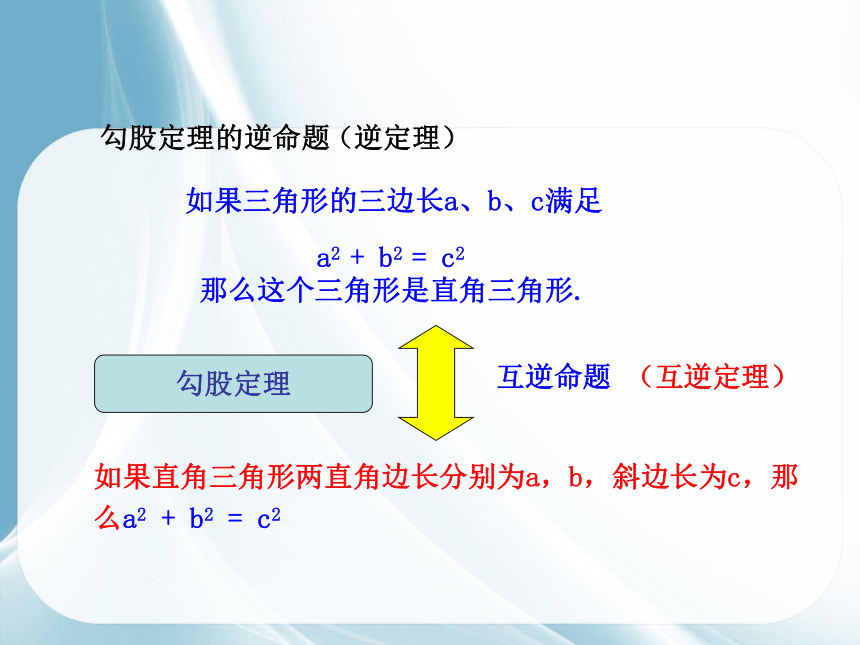
勾股定理的逆命题
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
互逆命题
(逆定理)
(互逆定理)
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2 + b2 = c2
请指出下列命题的逆命题,
(1)两直线平行,同位角相等.
(2)对顶角相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应边相等.
解:(1)同位角相等,两直线平行.
(2)相等的角是对顶角.
(3)如果两个实数的绝对值相等,那么它们相等.
(4)三边对应相等的两个三角形全等.
【例1】 判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17; (2)a=13, b=14,c=15.
【解析】(1)
【例2】 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【解析】根据题意画出图,如图所示.
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
因为242+182=302,即PQ2+PR2=QR2,
所以∠QPR=90°.
由“远航”号沿东北方向航行可知,∠QPS=45°.
所以∠RPS=45°,即“海天”号沿西北方向航行.
(3a) (4a) (5a)
2 2 2
+ =
\
Q
这
个
三
角
形
是
直
角
三
角
形
.
【例3 】在很久很久以前,古埃及人把一根长绳打上等距离的13个结,然后用桩钉钉成一个三角形 (如图) ,你知道这个三角形是什么形状吗?并说明理由.
【解析】这个三角形是直角三角形.
理由:设两个结的距离为a,则三边分别为3a,4a,5a.
1.工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定.你能测出这个零件是否合格吗?(身边只有刻度尺)
A
B
C
测量AB、BC、AC的长,看是否满足其中两边的平方和等于第三边的平方.
2.判断下列△ABC是不是直角三角形?
(2) a=15 b=20 c=25
(1) a=1 b=2 c=
(3) a:b:c=3:4:5
是
是
是
3.观察下列表格:
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
…
…
13、b、c
132=b+c
能够成为直角三角形三条边长的三个正整数,称为勾股数.
请你结合该表格及相关知识,求出b、c的值.
即b=_________, c=
84
85
4.如果△ABC的三边长分别为a、b、c且满足a2+b2+c2+50=6a+8b+10c,判定△ABC的形状.
这个三角形是直角三角形.
1.已知三角形的三边长为a、b、c,如果
(a-5)2+|b-12|+c2-26c+169=0,则△ABC是( )
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.不是直角三角形
【解析】选C.∵(a-5)2+|b-12|+c2-26c+169=0,
即(a-5)2+|b-12|+(c-13)2=0.
∴a=5,b=12,c=13.
又∵52+122=132,即a2+b2=c2.
∴△ABC是以c为斜边的直角三角形.
2.“全等三角形的面积相等”的逆命题是_______,它是______命题.(填“真”或“假”)
【解析】如一个直角三角形的面积等于一个锐角三角形的面积,这两个三角形不全等,故是假命题.
答案:面积相等的两个三角形全等 假
3. 已知:如图,在△ABC中,D
为边BC上的一点,AB=13,AD=12,AC=
15,BD=5.求△ABC的面积.
【解析】在△ABD中,由于BD2+AD2=AB2,
∴△ABD是直角三角形,
∴AD⊥BC,由于AC=15,AD=12,
在Rt△ADC中,
∴S△ABC= BC×AD= (BD+DC)×AD= ×(5+9)×12=84.
DC= 15-12 =9,
2 2
1
2
1
2
1
2
通过本课时的学习,需要我们
1.了解勾股定理的逆定理,并理解其证明方法.
2.会利用勾股定理的逆定理,判定直角三角形.
3.理解原命题、逆命题、逆定理的概念及关系.
直角三角形
三边关系
勾股定理
勾股定理逆定理
2.会利用勾股定理的逆定理,判定直角三角形.
1.了解勾股定理的逆定理,并理解其证明方法.
3.理解原命题、逆命题、逆定理的概念及关系.
1.画图:画出边长分别是下列各组数的三角形(单位:厘米).
A:3、4、3 ;B:3、4、5;C:3、4、6;D:6、8、10
2.测量:用你的量角器分别测量一下上述各三角形的最大角的度数,并记录如下:A:____ B:____ C:____ D:____
3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______ C:______ D______
4.找规律:根据上述每个三角形所给的各组边长请你找出最长边的平方与其他两边的平方和之间的关系.
A:_____ B:_____ C:_____ D:______
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
你的猜想是_____________.
猜想:三角形的三边长a、b、c满足:a2 + b2 = c2,那么这个三角形是直角三角形.
已知:在
c
a
b
B
C
A
△ABC中,AB=c,BC=a,CA=b,
且a2+b2=c2 .
求证:
△ ABC是直角三角形.
已知:在△ABC中,AB=c,BC=a,CA=b,并且
证明:作?
在△ABC和△
∴?ABC
∠C=∠
a
b
(如图)求证:∠C=90°.
使∠
则有
中,
△
=90°.
≌
=90°,
A
B
b
c
C
a
B C a, C A b,
1 1 1 1
= =
A B a b ,BC B C , CA C A ,
2 2 2
1 1 1 1 1 1
= + = =
+ =
A B c, AB A B .
\ = \ =
a b c ,
2 2 2
1 1 1 1
Q
BC B C ,
CA C A ,
AB A B ,
1 1
1 1
1 1
=
=
=
定理:如果三角形的三边长a,b,c满足a2 + b2 = c2,那么这个三角形是直角三角形.
a2 + b2 = c2
题设
结论
直角三角形
直角三角形
a2 + b2 = c2
题设和结论正好相反的两个命题,叫做互逆命题
其中一个叫做原命题,另一个叫做原命题的逆命题 .
勾股定理的逆命题
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
互逆命题
(逆定理)
(互逆定理)
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2 + b2 = c2
请指出下列命题的逆命题,
(1)两直线平行,同位角相等.
(2)对顶角相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应边相等.
解:(1)同位角相等,两直线平行.
(2)相等的角是对顶角.
(3)如果两个实数的绝对值相等,那么它们相等.
(4)三边对应相等的两个三角形全等.
【例1】 判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17; (2)a=13, b=14,c=15.
【解析】(1)
【例2】 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【解析】根据题意画出图,如图所示.
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
因为242+182=302,即PQ2+PR2=QR2,
所以∠QPR=90°.
由“远航”号沿东北方向航行可知,∠QPS=45°.
所以∠RPS=45°,即“海天”号沿西北方向航行.
(3a) (4a) (5a)
2 2 2
+ =
\
Q
这
个
三
角
形
是
直
角
三
角
形
.
【例3 】在很久很久以前,古埃及人把一根长绳打上等距离的13个结,然后用桩钉钉成一个三角形 (如图) ,你知道这个三角形是什么形状吗?并说明理由.
【解析】这个三角形是直角三角形.
理由:设两个结的距离为a,则三边分别为3a,4a,5a.
1.工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定.你能测出这个零件是否合格吗?(身边只有刻度尺)
A
B
C
测量AB、BC、AC的长,看是否满足其中两边的平方和等于第三边的平方.
2.判断下列△ABC是不是直角三角形?
(2) a=15 b=20 c=25
(1) a=1 b=2 c=
(3) a:b:c=3:4:5
是
是
是
3.观察下列表格:
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
…
…
13、b、c
132=b+c
能够成为直角三角形三条边长的三个正整数,称为勾股数.
请你结合该表格及相关知识,求出b、c的值.
即b=_________, c=
84
85
4.如果△ABC的三边长分别为a、b、c且满足a2+b2+c2+50=6a+8b+10c,判定△ABC的形状.
这个三角形是直角三角形.
1.已知三角形的三边长为a、b、c,如果
(a-5)2+|b-12|+c2-26c+169=0,则△ABC是( )
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.不是直角三角形
【解析】选C.∵(a-5)2+|b-12|+c2-26c+169=0,
即(a-5)2+|b-12|+(c-13)2=0.
∴a=5,b=12,c=13.
又∵52+122=132,即a2+b2=c2.
∴△ABC是以c为斜边的直角三角形.
2.“全等三角形的面积相等”的逆命题是_______,它是______命题.(填“真”或“假”)
【解析】如一个直角三角形的面积等于一个锐角三角形的面积,这两个三角形不全等,故是假命题.
答案:面积相等的两个三角形全等 假
3. 已知:如图,在△ABC中,D
为边BC上的一点,AB=13,AD=12,AC=
15,BD=5.求△ABC的面积.
【解析】在△ABD中,由于BD2+AD2=AB2,
∴△ABD是直角三角形,
∴AD⊥BC,由于AC=15,AD=12,
在Rt△ADC中,
∴S△ABC= BC×AD= (BD+DC)×AD= ×(5+9)×12=84.
DC= 15-12 =9,
2 2
1
2
1
2
1
2
通过本课时的学习,需要我们
1.了解勾股定理的逆定理,并理解其证明方法.
2.会利用勾股定理的逆定理,判定直角三角形.
3.理解原命题、逆命题、逆定理的概念及关系.
直角三角形
三边关系
勾股定理
勾股定理逆定理
