18.2.3 正方形 课件(共24张PPT)
文档属性
| 名称 | 18.2.3 正方形 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 09:06:52 | ||
图片预览


文档简介
18.2.3 正方形
2、理解正方形与平行四边形、矩形、菱形的联系和区别.
1、掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
定义
边
角
对 角 线
对 称 性
平行
四边形
矩 形
菱 形
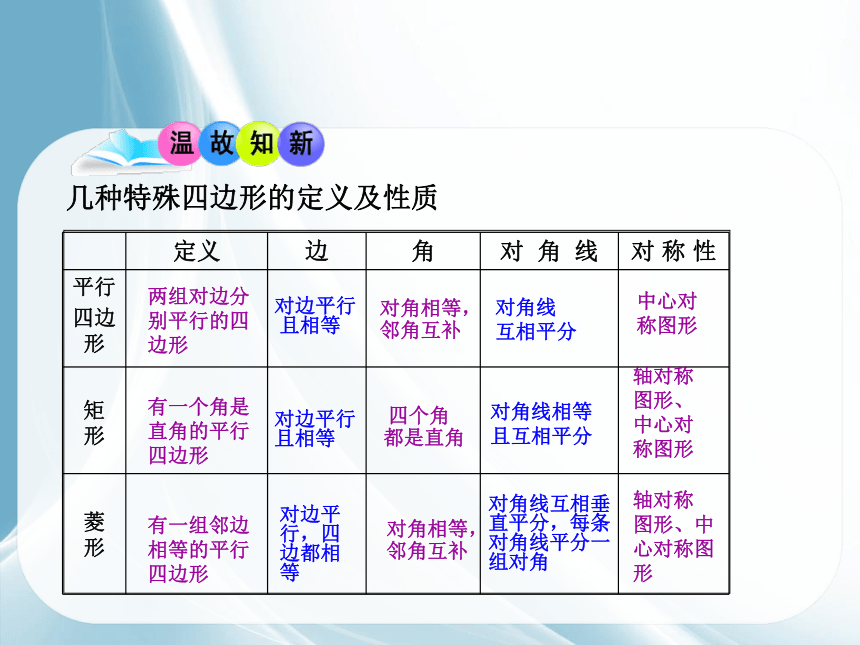
几种特殊四边形的定义及性质
对边平行
且相等
对边平行且相等
对边平行,四边都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,邻角互补
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
中心对
称图形
轴对称
图形、
中心对
称图形
轴对称
图形、中心对称图形
两组对边分
别平行的四
边形
有一个角是
直角的平行
四边形
有一组邻边
相等的平行
四边形
矩 形
〃
〃
正方形
邻边
相等
〃
〃
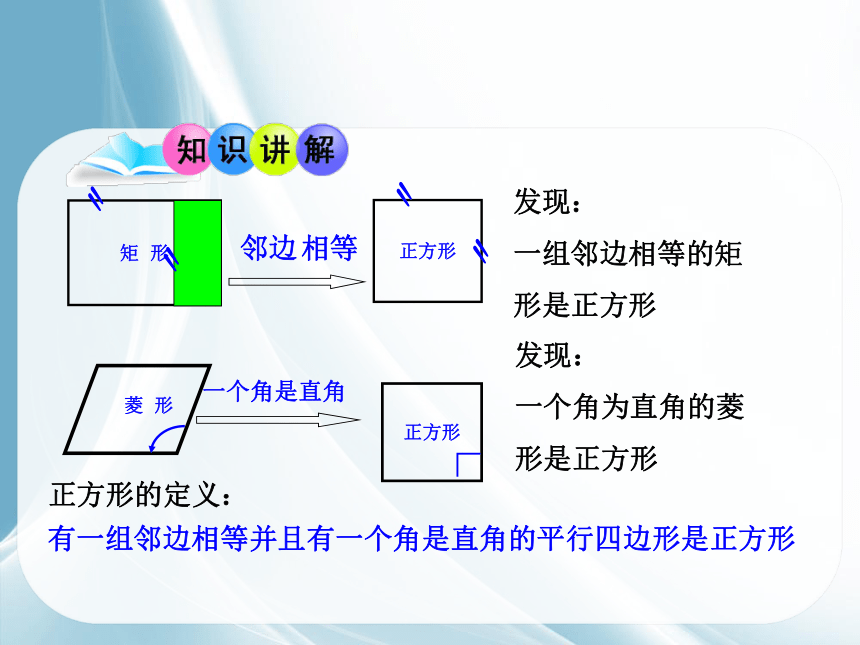
发现:
一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形是正方形
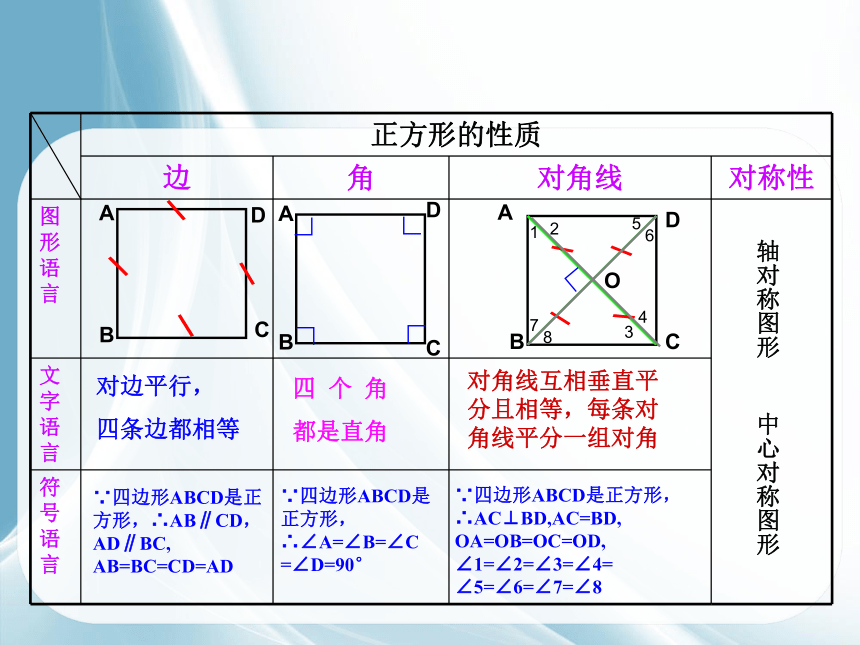
正方形的性质
边
角
对角线
对称性
图形语言
文
字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形,∴AB∥CD, AD∥BC, AB=BC=CD=AD
∵四边形ABCD是
正方形,
∴∠A=∠B=∠C
=∠D=90°
∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1=∠2=∠3=∠4=
∠5=∠6=∠7=∠8
轴对称图形 中心对称图形
1
2
3
4
5
6
7
8
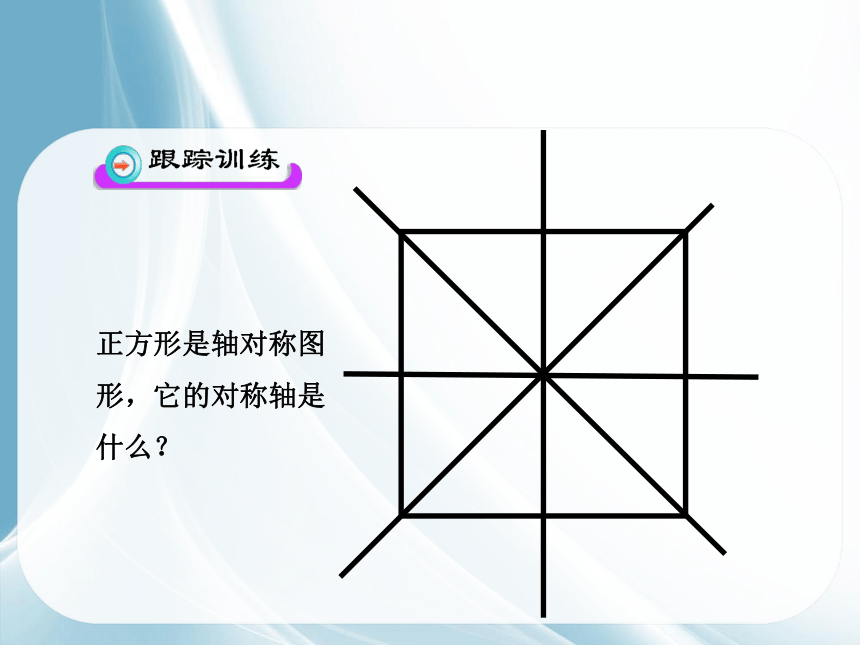
正方形是轴对称图形,它的对称轴是什么?
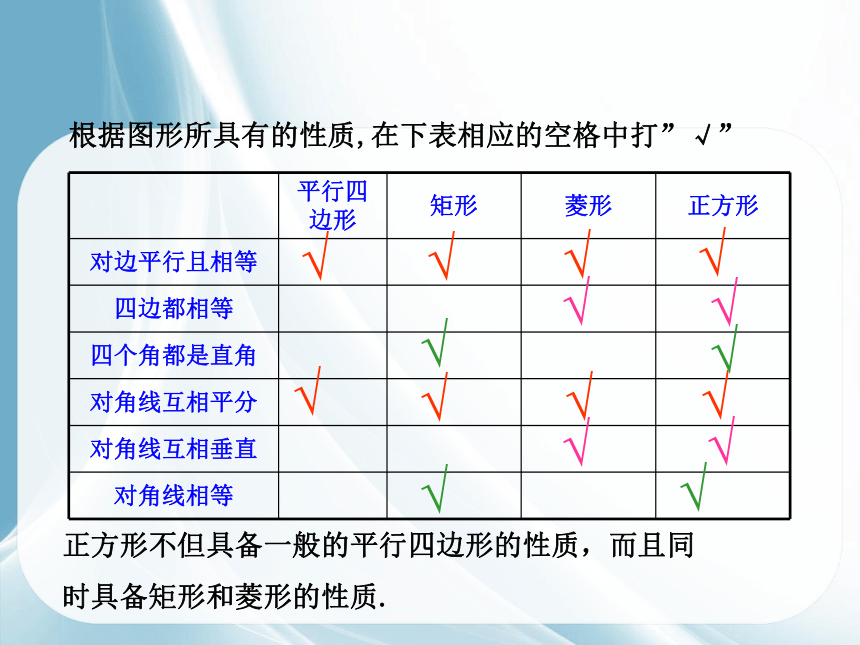
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质.
√
√
√
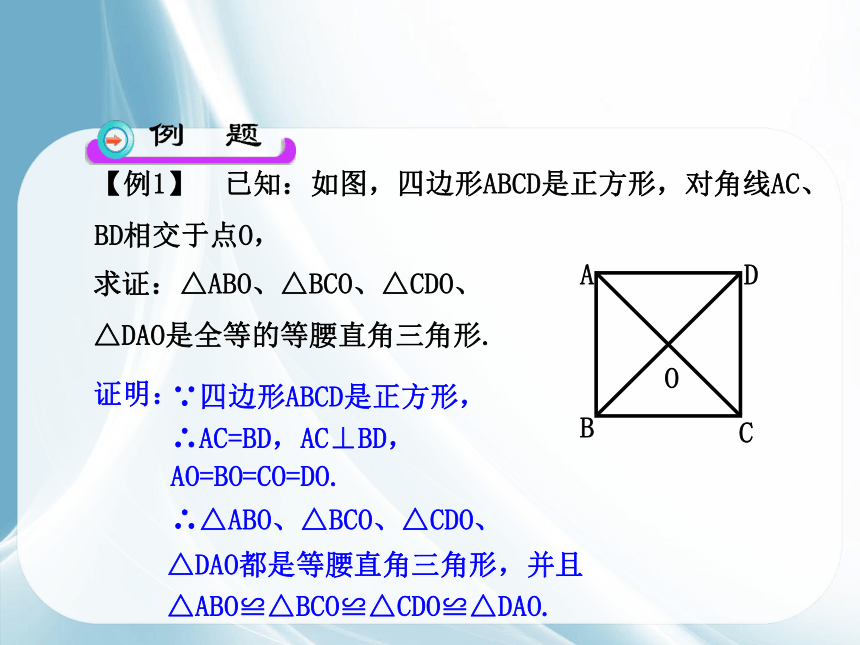
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
【例1】 已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O,
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
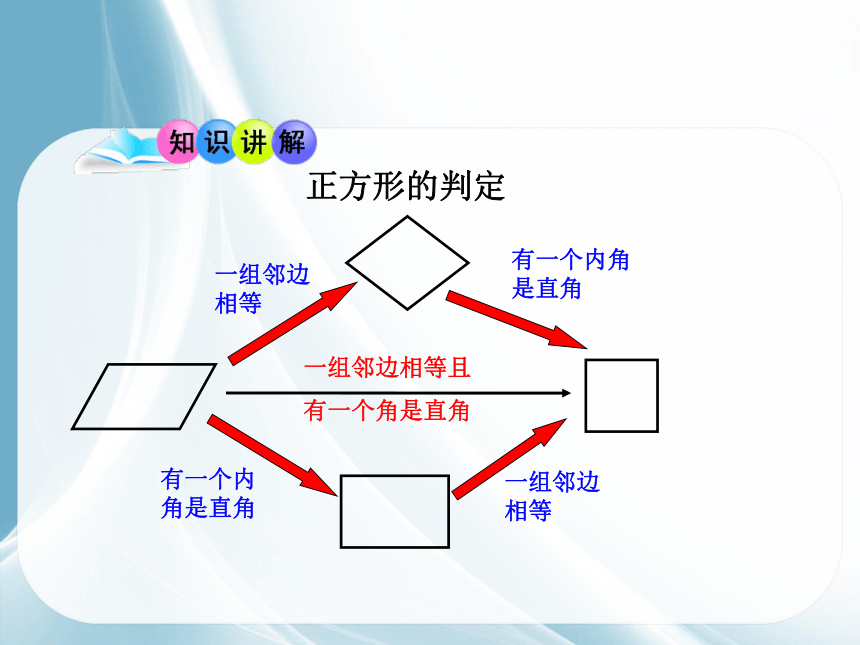
一组邻边相等
有一个内角是直角
一组邻边相等
有一个内角是直角
正方形的判定
一组邻边相等且
有一个角是直角
1.从长方形木板中怎样截出最大的正方形木板?
2.现有一条方巾,想请同学们帮助检验一下方巾是否是正方形的.怎样检验?
证明:∵ 四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=AD=DC=BC.
又∵ AE=BF=CG=DH,
∴AB-AE=AD-DH=DC-CG=BC-BF.
即BE=AH=DG=CF.
∴△AEH≌△BFE≌△CGF ≌△DHG.
EH=EF=FG=HG.∵∠1=∠3,
又∠3+∠2 =90°,
∠1+∠2=90°,
∴∠EFG =90°,∴ 四边形EFGH是正方形.
A
B
c
D
E
F
G
H
1
2
3
3、已知:正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
m .
40
=
-
=
2
BE
2
CE
BC
∴
AC AB BC
40 2 m.
= + =
2 2
∴
4、ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测EC=50 m,EB=30 m,这块场地的面积和对角线长分别是多少?
A
D
B
C
E
解:
连接AC.
∵ 四边形ABCD是正方形,
∴ ∠B=90°,AB=BC.
∵ EC=50 m,EB=30 m,
∴ S正方形ABCD=(40 )2=1600(m2).
5、在一块正方形的花坛上,欲修建两条笔直的小路使得两条笔直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
6.你能用恰当的方式表示出平行四边形、矩形、菱形、正方形之间的包含关系吗?
平行四边形
矩形
菱形
正
方
形
能
1. 下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
【解析】选D.有一个角是直角的平行四边形可能是矩形.
2. 如图,四边形ABCD是正方形,延长AB
到E,使AE=AC,则∠BCE的度数是_______.
【解析】∵四边形ABCD是正方形,
∴∠CAE=45°,∠ABC=90°.
又∵AE=AC,∴∠E=∠ACE=67.5°,
∴∠BCE=90°-∠E=90°-67.5°=22.5°.
答案:22.5
3.如图,点P是正方形ABCD的对角线BD上的一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD= EC.其中正确结论的序号是_____.
2
答案:①②④⑤
4. 已知线段AB的长为a,以AB为边,在AB的下方作正方形ACDB.取AB边上一点E,以AE为边在AB的上方作正方形AENM.过E作EF⊥CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,则AE的长为_________________.
【解析】设AE=x,则x2=a(a-x), 即x2+ax-a2=0,
所以x1= ,x2= ,又AE的长为正,
x2不合题意舍去.
答案:
5. 如图,在正方形ABCD中,G是BC上的任意一点(G与B、C两点不重合),E、F是AG上的两点(E、F与A、G两点不重合),若AF=BF+EF,∠1=∠2,请判断线段DE与BF有怎样的位置关系,并证明你的结论.
【解析】根据题目条件可判断DE∥BF.
证明如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠2=90°.
∵AF=AE+EF,又AF=BF+EF,
∴AE=BF.
∵∠1=∠2,∴△ABF≌△DAE(SAS),
∴∠AFB=∠DEA,∠BAF=∠ADE.
∴∠ADE+∠2=90°,
∴∠AED=∠BFA=90°,
∴DE∥BF.
6. 如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
(1)请判断四边形EFGH的形状?并说明为什么.
(2)要使四边形EFGH为正方形,那么四边形ABCD的对角线应该有怎样的情况?
【解析】(1)四边形EFGH是平行四边形.
连接AC,
∵E、F分别是AB、BC的中点,
∴EF∥AC,EF= AC.
同理HG∥AC,HG= AC.
∴EF HG,
∴四边形EFGH是平行四边形.
(2)四边形ABCD的对角线垂直且相等.
通过本课时的学习,需要我们
1、掌握正方形的定义、性质、判定.
2、了解正方形、矩形、菱形、平行四边形间的关
系,认识它们之间的联系和区别.
3、能综合利用正方形的性质与判定解决有关的证
明与计算.
2、理解正方形与平行四边形、矩形、菱形的联系和区别.
1、掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
定义
边
角
对 角 线
对 称 性
平行
四边形
矩 形
菱 形
几种特殊四边形的定义及性质
对边平行
且相等
对边平行且相等
对边平行,四边都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,邻角互补
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
中心对
称图形
轴对称
图形、
中心对
称图形
轴对称
图形、中心对称图形
两组对边分
别平行的四
边形
有一个角是
直角的平行
四边形
有一组邻边
相等的平行
四边形
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形是正方形
正方形的性质
边
角
对角线
对称性
图形语言
文
字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形,∴AB∥CD, AD∥BC, AB=BC=CD=AD
∵四边形ABCD是
正方形,
∴∠A=∠B=∠C
=∠D=90°
∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1=∠2=∠3=∠4=
∠5=∠6=∠7=∠8
轴对称图形 中心对称图形
1
2
3
4
5
6
7
8
正方形是轴对称图形,它的对称轴是什么?
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质.
√
√
√
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
【例1】 已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O,
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
一组邻边相等
有一个内角是直角
一组邻边相等
有一个内角是直角
正方形的判定
一组邻边相等且
有一个角是直角
1.从长方形木板中怎样截出最大的正方形木板?
2.现有一条方巾,想请同学们帮助检验一下方巾是否是正方形的.怎样检验?
证明:∵ 四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=AD=DC=BC.
又∵ AE=BF=CG=DH,
∴AB-AE=AD-DH=DC-CG=BC-BF.
即BE=AH=DG=CF.
∴△AEH≌△BFE≌△CGF ≌△DHG.
EH=EF=FG=HG.∵∠1=∠3,
又∠3+∠2 =90°,
∠1+∠2=90°,
∴∠EFG =90°,∴ 四边形EFGH是正方形.
A
B
c
D
E
F
G
H
1
2
3
3、已知:正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
m .
40
=
-
=
2
BE
2
CE
BC
∴
AC AB BC
40 2 m.
= + =
2 2
∴
4、ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测EC=50 m,EB=30 m,这块场地的面积和对角线长分别是多少?
A
D
B
C
E
解:
连接AC.
∵ 四边形ABCD是正方形,
∴ ∠B=90°,AB=BC.
∵ EC=50 m,EB=30 m,
∴ S正方形ABCD=(40 )2=1600(m2).
5、在一块正方形的花坛上,欲修建两条笔直的小路使得两条笔直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
6.你能用恰当的方式表示出平行四边形、矩形、菱形、正方形之间的包含关系吗?
平行四边形
矩形
菱形
正
方
形
能
1. 下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
【解析】选D.有一个角是直角的平行四边形可能是矩形.
2. 如图,四边形ABCD是正方形,延长AB
到E,使AE=AC,则∠BCE的度数是_______.
【解析】∵四边形ABCD是正方形,
∴∠CAE=45°,∠ABC=90°.
又∵AE=AC,∴∠E=∠ACE=67.5°,
∴∠BCE=90°-∠E=90°-67.5°=22.5°.
答案:22.5
3.如图,点P是正方形ABCD的对角线BD上的一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD= EC.其中正确结论的序号是_____.
2
答案:①②④⑤
4. 已知线段AB的长为a,以AB为边,在AB的下方作正方形ACDB.取AB边上一点E,以AE为边在AB的上方作正方形AENM.过E作EF⊥CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,则AE的长为_________________.
【解析】设AE=x,则x2=a(a-x), 即x2+ax-a2=0,
所以x1= ,x2= ,又AE的长为正,
x2不合题意舍去.
答案:
5. 如图,在正方形ABCD中,G是BC上的任意一点(G与B、C两点不重合),E、F是AG上的两点(E、F与A、G两点不重合),若AF=BF+EF,∠1=∠2,请判断线段DE与BF有怎样的位置关系,并证明你的结论.
【解析】根据题目条件可判断DE∥BF.
证明如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠2=90°.
∵AF=AE+EF,又AF=BF+EF,
∴AE=BF.
∵∠1=∠2,∴△ABF≌△DAE(SAS),
∴∠AFB=∠DEA,∠BAF=∠ADE.
∴∠ADE+∠2=90°,
∴∠AED=∠BFA=90°,
∴DE∥BF.
6. 如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
(1)请判断四边形EFGH的形状?并说明为什么.
(2)要使四边形EFGH为正方形,那么四边形ABCD的对角线应该有怎样的情况?
【解析】(1)四边形EFGH是平行四边形.
连接AC,
∵E、F分别是AB、BC的中点,
∴EF∥AC,EF= AC.
同理HG∥AC,HG= AC.
∴EF HG,
∴四边形EFGH是平行四边形.
(2)四边形ABCD的对角线垂直且相等.
通过本课时的学习,需要我们
1、掌握正方形的定义、性质、判定.
2、了解正方形、矩形、菱形、平行四边形间的关
系,认识它们之间的联系和区别.
3、能综合利用正方形的性质与判定解决有关的证
明与计算.
