19.1.1 变量与函数 课件(共15张PPT)
文档属性
| 名称 | 19.1.1 变量与函数 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 09:12:16 | ||
图片预览





文档简介
19.1.1 变量与函数
第十九章 一次函数
19.1 函数
1.通过探索具体问题中的数量关系和变化规律来了解常
量、变量的意义;
2.学会用含一个变量的代数式表示另一个变量;
3.结合实例,理解函数的概念以及自变量的意义;在理解
掌握函数概念的基础上,确定函数关系式;
4.会根据函数解析式和实际意义确定自变量的取值范围.
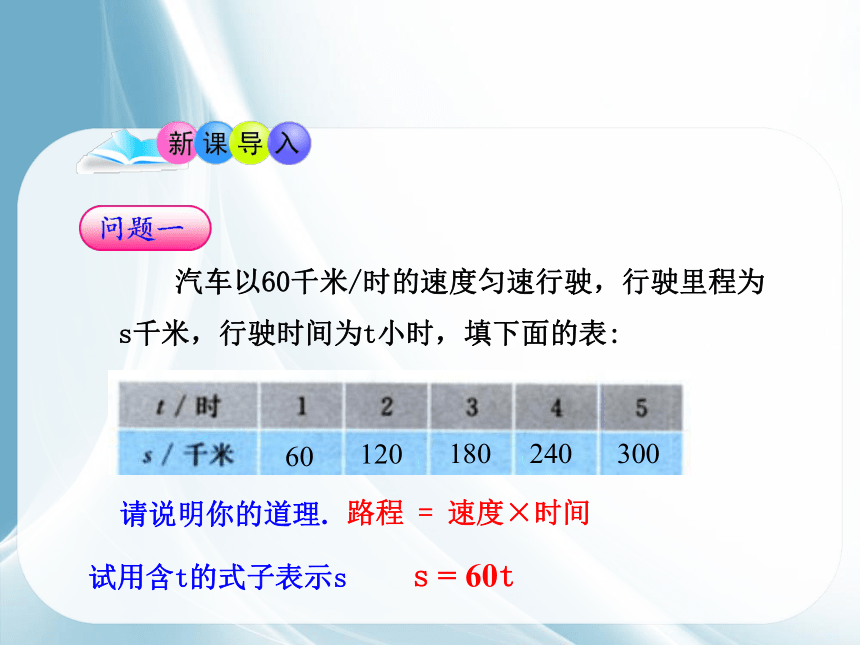
汽车以60千米/时的速度匀速行驶,行驶里程为
s千米,行驶时间为t小时,填下面的表:
请说明你的道理.
路程 = 速度×时间
试用含t的式子表示s
s = 60t
60
120
180
240
300
电影票的售价为10元/张,第一场售出150张票,
第二场场售出205张票,第三场售出310张票,三场电影票的票房收入各多少元?
第一场票房收入 = 10×150 = 1500 (元)
第二场票房收入 = 10×205 = 2050 (元)
第三场票房收入 = 10×310 = 3100 (元)
若设一场电影售出x张票,票房收入为y元,怎样用含x的式子表示y?
y = 10x
请说明道理:
票房收入= 票价×售票张数
在一根弹簧的下端挂重物,改变并记录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律.如果弹簧原长为10 cm,每1千克重物使弹簧伸长0.5 cm,怎样用含重物质量x(单位:kɡ)的式子表示受力后的弹簧长度 L(单位:cm)?
挂重2千克时弹簧长=10+0.5×2=11(cm)
挂重3千克时弹簧长=10+0.5×3=11.5(cm)
挂重x千克时弹簧长=(10+0.5×x)cm
L=10+0.5x
分析:
挂重1千克时弹簧长=10+0.5×1=10.5(cm)
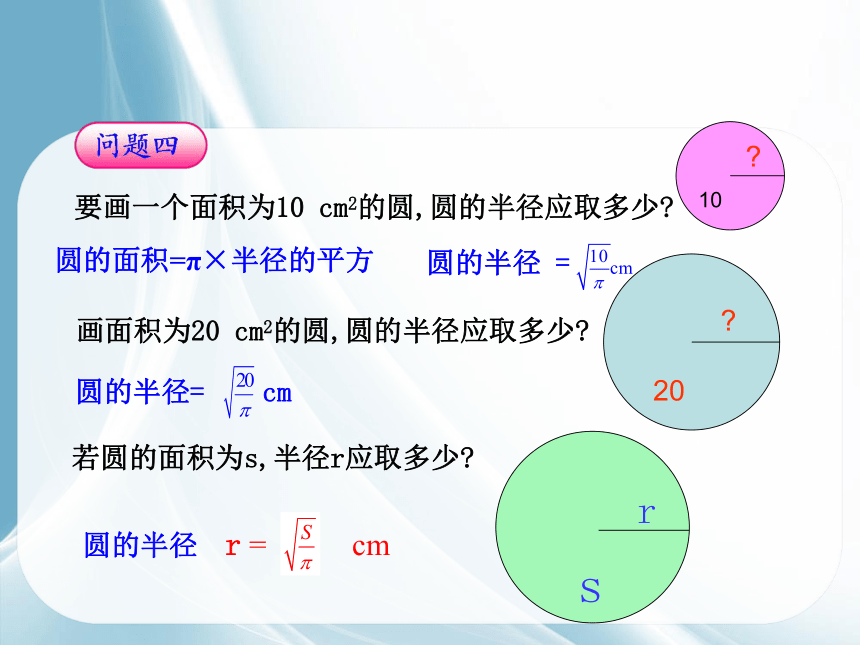
要画一个面积为10 cm2的圆,圆的半径应取多少?
圆的半径 =
圆的面积=π×半径的平方
画面积为20 cm2的圆,圆的半径应取多少?
圆的半径= cm
若圆的面积为s,半径r应取多少?
r = cm
圆的半径
?
10
20
?
r
s
用10 m长的绳子围成长方形,长方形的长为3 m时面积
为多少?
当长方形的长为3 m时,面积=3×[(10-2×3)÷2]=6 m2
想一想:改变长方形的长,观察长方形的面积怎样变化?
设长方形的长为 x m,面积为S m2,怎样用含x的式子
表示 S ?
S=x[(10-2x)÷2]
S=
x(10-2x)
=x(5-x)
2
1
(1)s=60t
(3)L=10+0.5x
(2)y=10x
在一个变化过程中,数值发生变化的量为变量.
变量:
在一个变化过程中,数值始终不变的量为常量.
常量:
s
(4)r
=
p
1
(5) S x(10 2x) x(5 x)
2
= - = -
共同特征:
1.都有两个变量.
2.其中的一个变量取定一个值,另一个变量的
值也唯一确定.
我们称另一个变量是一个变量的函数.
指出前面四个问题中的自变量与函数.
1.“票房收入问题”中,y=10x,对于x的每一个值,y都有
的值与之对应,所以 是自变量,y是x的函数.
2.“行程问题”中s=60t,对于t的每一个值,s都有_____
的值与之对应,所以 是自变量, 是 的函数.
归纳:如果有两个变量,对于x的每一个值,y都有
的值与之对应,称x是 ,y是x的 .
唯一
x
唯一
t
s
t
唯一
自变量
函数
1.某位教师为学生购买数学辅导书,书的单价是4元,则
总金额y(元)与学生数n(个)的关系式是 .
其中的变量是 .常量是 .
2.计划购买50元的乒乓球,所能购买的总数n(个)与单价 a(元)的关系式为 .其中的变量是 _ ,
常量是 .
3.圆的周长公式 ,这里的变量是 ,常量是 .
y=4n
n和y
4
n=
a和n
50
r和C
2π
4.三角形的底边为5,高h可以任意伸缩,三角形的面积S也随之发生了变化.
【解析】面积S随高h变化的关系式S = ,其中常量是 ,变量是 , 是自变量,
是 的函数.
h和S
h
S
h
5.写出下列问题中的关系式:
(1)用周长为20的铁丝所围的长方形的长x与面积S的关系.
(2)直角三角形中一个锐角A与另一个锐角B之间的关系.
(3)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
A=90°-B
y=30-0.5t
通过本课时的学习,需要我们:
1.了解具体问题中常量、变量的意义;
2.学会用含一个变量的代数式表示另一个变量;
3.结合实例,理解函数的概念以及自变量的意义;在理解
掌握函数概念的基础上,确定函数关系式.
第十九章 一次函数
19.1 函数
1.通过探索具体问题中的数量关系和变化规律来了解常
量、变量的意义;
2.学会用含一个变量的代数式表示另一个变量;
3.结合实例,理解函数的概念以及自变量的意义;在理解
掌握函数概念的基础上,确定函数关系式;
4.会根据函数解析式和实际意义确定自变量的取值范围.
汽车以60千米/时的速度匀速行驶,行驶里程为
s千米,行驶时间为t小时,填下面的表:
请说明你的道理.
路程 = 速度×时间
试用含t的式子表示s
s = 60t
60
120
180
240
300
电影票的售价为10元/张,第一场售出150张票,
第二场场售出205张票,第三场售出310张票,三场电影票的票房收入各多少元?
第一场票房收入 = 10×150 = 1500 (元)
第二场票房收入 = 10×205 = 2050 (元)
第三场票房收入 = 10×310 = 3100 (元)
若设一场电影售出x张票,票房收入为y元,怎样用含x的式子表示y?
y = 10x
请说明道理:
票房收入= 票价×售票张数
在一根弹簧的下端挂重物,改变并记录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律.如果弹簧原长为10 cm,每1千克重物使弹簧伸长0.5 cm,怎样用含重物质量x(单位:kɡ)的式子表示受力后的弹簧长度 L(单位:cm)?
挂重2千克时弹簧长=10+0.5×2=11(cm)
挂重3千克时弹簧长=10+0.5×3=11.5(cm)
挂重x千克时弹簧长=(10+0.5×x)cm
L=10+0.5x
分析:
挂重1千克时弹簧长=10+0.5×1=10.5(cm)
要画一个面积为10 cm2的圆,圆的半径应取多少?
圆的半径 =
圆的面积=π×半径的平方
画面积为20 cm2的圆,圆的半径应取多少?
圆的半径= cm
若圆的面积为s,半径r应取多少?
r = cm
圆的半径
?
10
20
?
r
s
用10 m长的绳子围成长方形,长方形的长为3 m时面积
为多少?
当长方形的长为3 m时,面积=3×[(10-2×3)÷2]=6 m2
想一想:改变长方形的长,观察长方形的面积怎样变化?
设长方形的长为 x m,面积为S m2,怎样用含x的式子
表示 S ?
S=x[(10-2x)÷2]
S=
x(10-2x)
=x(5-x)
2
1
(1)s=60t
(3)L=10+0.5x
(2)y=10x
在一个变化过程中,数值发生变化的量为变量.
变量:
在一个变化过程中,数值始终不变的量为常量.
常量:
s
(4)r
=
p
1
(5) S x(10 2x) x(5 x)
2
= - = -
共同特征:
1.都有两个变量.
2.其中的一个变量取定一个值,另一个变量的
值也唯一确定.
我们称另一个变量是一个变量的函数.
指出前面四个问题中的自变量与函数.
1.“票房收入问题”中,y=10x,对于x的每一个值,y都有
的值与之对应,所以 是自变量,y是x的函数.
2.“行程问题”中s=60t,对于t的每一个值,s都有_____
的值与之对应,所以 是自变量, 是 的函数.
归纳:如果有两个变量,对于x的每一个值,y都有
的值与之对应,称x是 ,y是x的 .
唯一
x
唯一
t
s
t
唯一
自变量
函数
1.某位教师为学生购买数学辅导书,书的单价是4元,则
总金额y(元)与学生数n(个)的关系式是 .
其中的变量是 .常量是 .
2.计划购买50元的乒乓球,所能购买的总数n(个)与单价 a(元)的关系式为 .其中的变量是 _ ,
常量是 .
3.圆的周长公式 ,这里的变量是 ,常量是 .
y=4n
n和y
4
n=
a和n
50
r和C
2π
4.三角形的底边为5,高h可以任意伸缩,三角形的面积S也随之发生了变化.
【解析】面积S随高h变化的关系式S = ,其中常量是 ,变量是 , 是自变量,
是 的函数.
h和S
h
S
h
5.写出下列问题中的关系式:
(1)用周长为20的铁丝所围的长方形的长x与面积S的关系.
(2)直角三角形中一个锐角A与另一个锐角B之间的关系.
(3)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
A=90°-B
y=30-0.5t
通过本课时的学习,需要我们:
1.了解具体问题中常量、变量的意义;
2.学会用含一个变量的代数式表示另一个变量;
3.结合实例,理解函数的概念以及自变量的意义;在理解
掌握函数概念的基础上,确定函数关系式.
