20.1.2 中位数和众数 课件(共24张PPT)
文档属性
| 名称 | 20.1.2 中位数和众数 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1001.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 09:26:04 | ||
图片预览






文档简介
20.1.2 中位数和众数
2.理解中位数和众数的意义和作用,了解平均数、中位数、众数在描述数据时的差异.
1.认识中位数和众数,并会求出一组数据中的众数和中位数.
3.会利用中位数、众数分析数据信息做出决策.
某公司员工的月薪如下:
月薪(元)
45000
18000
10000
5500
5000
3400
3000
1000
人数
1
1
1
3
6
1
11
1
问题1:请大家仔细观察表格中的数据,讨论该公司的月平均工资是多少?
问题2:平均月工资能否客观地反映员工的实际收入?
问题3:再仔细观察表中的数据,你们认为用哪个数据反映一般职员的实际收入比较合适?
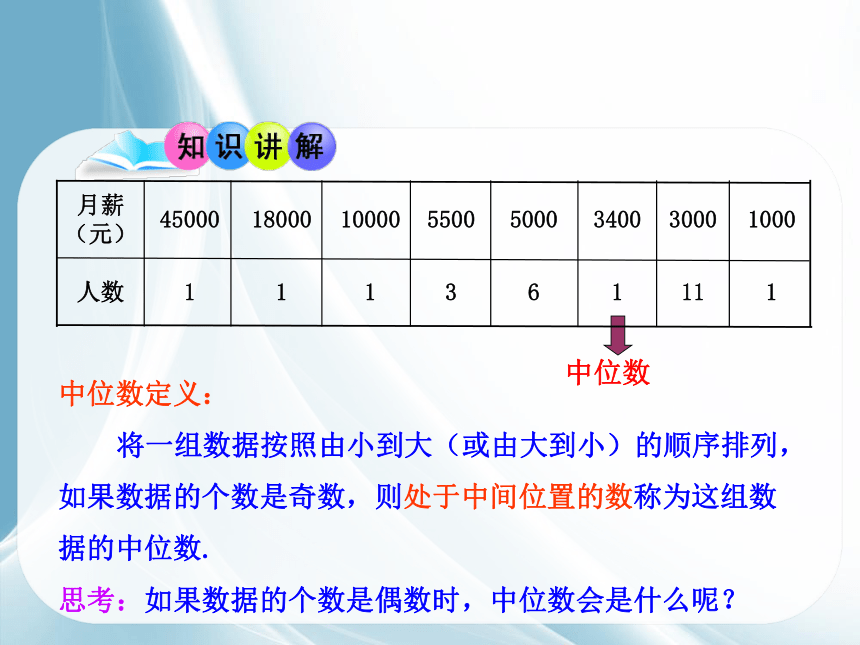
中位数
中位数定义:
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数称为这组数据的中位数.
思考:如果数据的个数是偶数时,中位数会是什么呢?
1
11
1
6
3
1
1
1
人数
1000
3000
3400
5000
5500
10000
18000
45000
月薪(元)
注意:1.求中位数要将一组数据按大小顺序进行排列,而不必计算,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序时,从小到大或从大到小都可以.
2.当数据个数为奇数时,中位数是这组数据中处于中间位置的一个数据;但当数据个数为偶数时,其中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等.
【例】 在一次男子马拉松长跑比赛中,抽得12名选手的成绩 (单位:分) 如下:
136 140 129 180 124 154
146 145 158 175 165 148.
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142分,他的成绩如何?
【解析】(1)147 (2)中等以下
1.某公司共有51名员工(包括经理1名),经理的工资高于其他员工的工资.今年经理的工资从去年的200000元增加到225000元,而其他员工的工资同去年一样,这样,这家公司所有员工今年工资的平均数和中位数与去年相比将会( )
A.平均数和中位数不变
B.平均数增加,中位数不变
C.平均数不变,中位数增加
D.平均数和中位数都增加
【解析】选B.平均数随着经理工资的增加而增加,由于其他
员工的工资不变,且低于经理的工资,所以中位数不变.
2.四次测试小丽每分钟做仰卧起坐的次数分别为:50、 45、48、47,遮住数据的中位数为 .
【解析】将这组数据按由小到大的顺序排列,最中间的两个数的平均数为 ,即为中位数.
答案:47.5
3. 2013年4月20日四川雅安市芦山县发生7.0级大地震后,湘江中学九年级(1)班的60名同学踊跃捐款.有15人每人捐30元、14人每人捐100元、10人每人捐70元、21人每人捐50元.在这次每人捐款的数值中,中位数是___.
【解析】将这组数据按由小到大的顺序排列,最中间的两个
数的平均数为 =50(元).
答案:50元
4.一组数据23、27、20、18、x、12,它的中位数
是21,则x的值是___.
【解析】由题意可得, 解得x=22.
答案:22
20 x
=21
2
+
,
定义:一组数据中出现次数最多的数据称为这组数据的众数.
注意:(1)众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.
(2)一组数据中的众数有时不只一个,如数据2、3、
-1、2、1、3中,2和3都出现了2次,它们都是这组数据的众数.
1.小丽在清点本班为四川雅安地震灾区的捐款时发现,全班同学捐款的钞票如下:100元的5张,50元的10张,10元的20张,5元的10张.在这些不同面额的钞票中,众数是( )元的钞票.
A.5 B.10 C.50 D.100
【解析】选B.捐款中10元的最多,即众数是10元的钞票。
2.为了解某班学生每天使用零花钱的情况,小红随机调查了15名同学,结果如下表:
则这15名同学每天使用零花钱的众数和中位数分别是( )
A.3,3 B.2,3 C.2,2 D.3,5
每天使用零花钱(单位:元)
1
2
3
5
6
人数
2
5
4
3
1
【解析】选B.出现次数最多的是2,即众数是2;
将这组数据按由小到大的顺序排列,最中间的
数是3,即中位数是3.
3. 某面包房,在一天内销售面包100个,各类面包销售量如下表:
面包种类
奶油
巧克力
豆沙
香稻
三色
椰茸
销售量
(个)
10
15
25
5
15
30
如果你是店主,你最关心的是______.
众数
1.某学习小组7位同学,为玉树地震灾区捐款,捐款金额分别为5元,10元,6元,6元,7元,8元,9元,则这组数据的中位数与众数分别为( )
A.6,6 B.7,6 C.7,8 D.6,8
【解析】选B.把这7个数从小到大排列为5, 6, 6, 7, 8, 9, 10.中间的一个数是7,有两个6,其他数都是一个,所以这组数据的中位数是7,众数是6.
2.中国2010年上海世博会充分体现“城市,让生活更美好”的主题.据统计5月1日至5月7日入园人数(单位:万人)分别为20.3,21.5,13.2,14.6,10.9,11.3,13.9.这组数据中的中位数和平均数分别为( )
A.14.6,15.1 B.14.65,15.0
C.13.9,15.1 D.13.9,15.0
【解析】选C.将这组数据按由小到大的顺序排列,最中间的
数为13.9,故中位数为13.9;这组数据的平均数为:
20.3+21.5+13.2+14.6+10.9+11.3+13.9
x = =15.1.
7
3. 为了参加市中学生篮球运动会,一支篮球队准备购买10双运动鞋,各种尺码统计如下表:
则这10双运动鞋尺码的众数和中位数分别为( )
A.25.5厘米,26厘米 B.26厘米,25.5厘米
C.25.5厘米,25.5厘米 D.26厘米,26厘米
【解析】选D.出现次数最多的是26厘米,故众数为26厘米;
中位数是最中间两个数的平均数 (厘米).
4.甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等,比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
(1)在图1中,“7分”所在扇形的圆心角等于_____.
(2)请你将图2的统计图补充完整.
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
【解析】(1)144°;
(2)如图:
(3)甲校的平均分为8.3分,中位数为7分;由于两校
平均分相等,乙校成绩的中位数大于甲校的中位数,所
以从平均分和中位数角度上判断,乙校的成绩较好.
(4)因为选8名学生参加市级口语团体赛,甲校得10分
的有8人,而乙校得10分的只有5人,所以应选甲校.
通过本课时的学习,需要我们:
1.会求出一组数据的众数和中位数.
2.理解中位数和众数的意义和作用,了解平均数、中位数、众数在描述数据时的差异.
3.会利用中位数、众数分析数据信息做出正确的决策.
4.中位数、众数都带单位.
2.理解中位数和众数的意义和作用,了解平均数、中位数、众数在描述数据时的差异.
1.认识中位数和众数,并会求出一组数据中的众数和中位数.
3.会利用中位数、众数分析数据信息做出决策.
某公司员工的月薪如下:
月薪(元)
45000
18000
10000
5500
5000
3400
3000
1000
人数
1
1
1
3
6
1
11
1
问题1:请大家仔细观察表格中的数据,讨论该公司的月平均工资是多少?
问题2:平均月工资能否客观地反映员工的实际收入?
问题3:再仔细观察表中的数据,你们认为用哪个数据反映一般职员的实际收入比较合适?
中位数
中位数定义:
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数称为这组数据的中位数.
思考:如果数据的个数是偶数时,中位数会是什么呢?
1
11
1
6
3
1
1
1
人数
1000
3000
3400
5000
5500
10000
18000
45000
月薪(元)
注意:1.求中位数要将一组数据按大小顺序进行排列,而不必计算,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序时,从小到大或从大到小都可以.
2.当数据个数为奇数时,中位数是这组数据中处于中间位置的一个数据;但当数据个数为偶数时,其中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等.
【例】 在一次男子马拉松长跑比赛中,抽得12名选手的成绩 (单位:分) 如下:
136 140 129 180 124 154
146 145 158 175 165 148.
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142分,他的成绩如何?
【解析】(1)147 (2)中等以下
1.某公司共有51名员工(包括经理1名),经理的工资高于其他员工的工资.今年经理的工资从去年的200000元增加到225000元,而其他员工的工资同去年一样,这样,这家公司所有员工今年工资的平均数和中位数与去年相比将会( )
A.平均数和中位数不变
B.平均数增加,中位数不变
C.平均数不变,中位数增加
D.平均数和中位数都增加
【解析】选B.平均数随着经理工资的增加而增加,由于其他
员工的工资不变,且低于经理的工资,所以中位数不变.
2.四次测试小丽每分钟做仰卧起坐的次数分别为:50、 45、48、47,遮住数据的中位数为 .
【解析】将这组数据按由小到大的顺序排列,最中间的两个数的平均数为 ,即为中位数.
答案:47.5
3. 2013年4月20日四川雅安市芦山县发生7.0级大地震后,湘江中学九年级(1)班的60名同学踊跃捐款.有15人每人捐30元、14人每人捐100元、10人每人捐70元、21人每人捐50元.在这次每人捐款的数值中,中位数是___.
【解析】将这组数据按由小到大的顺序排列,最中间的两个
数的平均数为 =50(元).
答案:50元
4.一组数据23、27、20、18、x、12,它的中位数
是21,则x的值是___.
【解析】由题意可得, 解得x=22.
答案:22
20 x
=21
2
+
,
定义:一组数据中出现次数最多的数据称为这组数据的众数.
注意:(1)众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.
(2)一组数据中的众数有时不只一个,如数据2、3、
-1、2、1、3中,2和3都出现了2次,它们都是这组数据的众数.
1.小丽在清点本班为四川雅安地震灾区的捐款时发现,全班同学捐款的钞票如下:100元的5张,50元的10张,10元的20张,5元的10张.在这些不同面额的钞票中,众数是( )元的钞票.
A.5 B.10 C.50 D.100
【解析】选B.捐款中10元的最多,即众数是10元的钞票。
2.为了解某班学生每天使用零花钱的情况,小红随机调查了15名同学,结果如下表:
则这15名同学每天使用零花钱的众数和中位数分别是( )
A.3,3 B.2,3 C.2,2 D.3,5
每天使用零花钱(单位:元)
1
2
3
5
6
人数
2
5
4
3
1
【解析】选B.出现次数最多的是2,即众数是2;
将这组数据按由小到大的顺序排列,最中间的
数是3,即中位数是3.
3. 某面包房,在一天内销售面包100个,各类面包销售量如下表:
面包种类
奶油
巧克力
豆沙
香稻
三色
椰茸
销售量
(个)
10
15
25
5
15
30
如果你是店主,你最关心的是______.
众数
1.某学习小组7位同学,为玉树地震灾区捐款,捐款金额分别为5元,10元,6元,6元,7元,8元,9元,则这组数据的中位数与众数分别为( )
A.6,6 B.7,6 C.7,8 D.6,8
【解析】选B.把这7个数从小到大排列为5, 6, 6, 7, 8, 9, 10.中间的一个数是7,有两个6,其他数都是一个,所以这组数据的中位数是7,众数是6.
2.中国2010年上海世博会充分体现“城市,让生活更美好”的主题.据统计5月1日至5月7日入园人数(单位:万人)分别为20.3,21.5,13.2,14.6,10.9,11.3,13.9.这组数据中的中位数和平均数分别为( )
A.14.6,15.1 B.14.65,15.0
C.13.9,15.1 D.13.9,15.0
【解析】选C.将这组数据按由小到大的顺序排列,最中间的
数为13.9,故中位数为13.9;这组数据的平均数为:
20.3+21.5+13.2+14.6+10.9+11.3+13.9
x = =15.1.
7
3. 为了参加市中学生篮球运动会,一支篮球队准备购买10双运动鞋,各种尺码统计如下表:
则这10双运动鞋尺码的众数和中位数分别为( )
A.25.5厘米,26厘米 B.26厘米,25.5厘米
C.25.5厘米,25.5厘米 D.26厘米,26厘米
【解析】选D.出现次数最多的是26厘米,故众数为26厘米;
中位数是最中间两个数的平均数 (厘米).
4.甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等,比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
(1)在图1中,“7分”所在扇形的圆心角等于_____.
(2)请你将图2的统计图补充完整.
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
【解析】(1)144°;
(2)如图:
(3)甲校的平均分为8.3分,中位数为7分;由于两校
平均分相等,乙校成绩的中位数大于甲校的中位数,所
以从平均分和中位数角度上判断,乙校的成绩较好.
(4)因为选8名学生参加市级口语团体赛,甲校得10分
的有8人,而乙校得10分的只有5人,所以应选甲校.
通过本课时的学习,需要我们:
1.会求出一组数据的众数和中位数.
2.理解中位数和众数的意义和作用,了解平均数、中位数、众数在描述数据时的差异.
3.会利用中位数、众数分析数据信息做出正确的决策.
4.中位数、众数都带单位.
