20.2 数据的波动程度 课件(共24张PPT)
文档属性
| 名称 | 20.2 数据的波动程度 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 09:28:39 | ||
图片预览








文档简介
20.2 数据的波动程度
2.理解方差概念的产生和形成的过程.
1.了解方差的定义和计算公式.
3.经历探索方差的应用过程,体会数据波动中的方差的求法.
为什么说新加坡是“四季温差不大”,而北京是“四季分明”呢?
甲,乙两名同学的测试成绩统计如下:
甲
85
90
90
90
95
乙
95
85
95
85
90
问题
80
85
90
95
100
成绩(分)
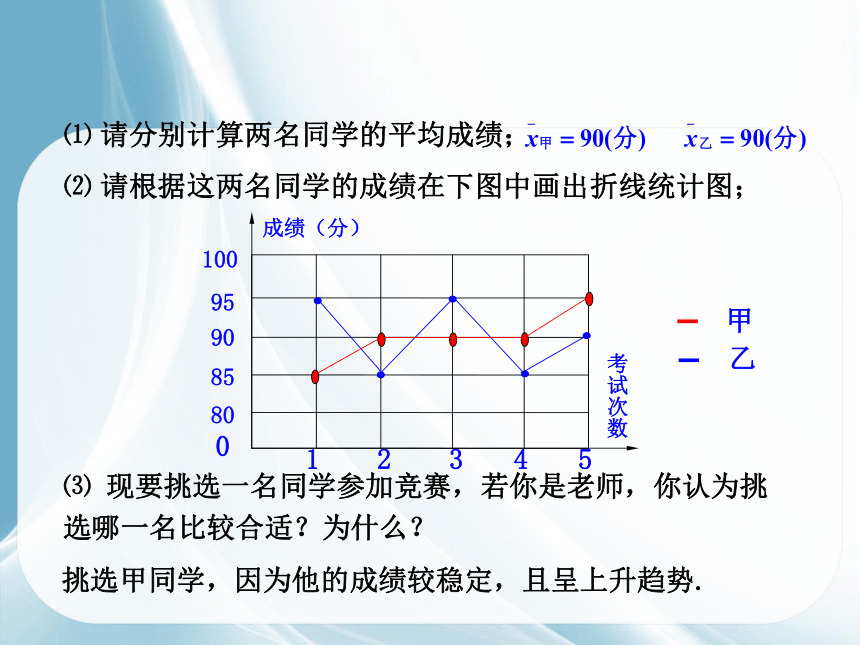
⑶ 现要挑选一名同学参加竞赛,若你是老师,你认为挑选哪一名比较合适?为什么?
⑴ 请分别计算两名同学的平均成绩;
⑵ 请根据这两名同学的成绩在下图中画出折线统计图;
0
1
2
3
4
5
考试次数
挑选甲同学,因为他的成绩较稳定,且呈上升趋势.
甲
乙
甲同学成绩与平均成绩的偏差的和:
乙同学成绩与平均成绩的偏差的和:
(85-90)+(90-90)+(90-90)+(90-90)+
(95-90)=
0
(95-90)+(85-90)+(95-90)+(85-90)+
(90-90)=
0
谁的稳定性好?应用什么数据来衡量?
甲同学成绩与平均成绩的偏差的平方和:
乙同学成绩与平均成绩的偏差的平方和:
(85-90)2+(90-90)2 +(90-90)2 +(90-90)2 +(95-
90)2 =
50
(95-90)2 +(85-90)2 +(95-90)2 +(85-90)2 +(90-90)2 =
100
谁的稳定性好?应用什么数据来衡量?
上述各偏差的平方和的大小还与什么有关?
——与考试次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性.
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x )2、(x2-x )2 、… 、(xn- x )2 ,那么我们用它们的平均数,即用
想一想
s2 = [(x1-x )2+(x2-x )2 +…+(xn-x )2 ]
1
n
为了刻画一组数据波动的大小,可以采用多种方
式.统计中通常采用下面的做法:设有n个数据x1,x2,…,
xn,各数据与它们的平均数的差的平方分别是 ,我们用它们的平均数,即用 来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作S2.
(x1-x)2,(x2-x)2, … ,(x-x)2
(x1-x)2,(x2-x)2, … ,(x-x)2
n
s 2= [ (x1-x)2,(x2-x)2, … ,(x-x)2]
n
n
1
讨论:(1)数据比较分散时,方差值怎样?
(2)数据比较集中时,方差值怎样?
(3)方差的大小与数据的波动性大小有怎样的关系?
结论:方差越大,数据的波动越大;
方差越小,数据的波动越小.
【例1】 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
甲团:163 164 164 165 165 166 166 167
乙团:163 165 165 166 166 167 168 168
哪个芭蕾舞团女演员的身高更整齐?
【解析】甲、乙两团演员的平均身高分别是
1、样本方差的作用是( )
A.表示总体的平均水平 B.表示样本的平均水平
C.准确表示总体的波动大小 D.表示样本的波动大小
3、在样本方差的计算公式
数字10 表示 ,数字20表示___________.
2、样本5、6、7、8、9的方差是 .
D
2
样本平均数
样本容量
ú
?
ù
ê
?
é
-
+
-
+
-
=
)
20
(
2
+
)
20
(
2
2
)
20
(
1
2
10
1
2
s
x
n
x
x
...
4、在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学
70
95
75
95
90
英语
80
85
90
85
85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数: 都是85 方差: ①数学 110; ②英语 10
建议:英语较稳定但要提高; 数学不够稳定有待努力进步!
品种
各实验田每公顷产量(单位:吨)
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
请为农科院选择玉米种子提出你的建议.
5、农科院对甲乙两种甜玉米各用10块实验田进行试验,得到两个品种每公顷产量的两组数据:
品种
各实验田每公顷产量(单位:吨)
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
甲、乙两种甜玉米的每公顷平均产量相差不是太大,但乙种
甜玉米的产量更稳定些,所以建议选择乙种玉米种子.
1.某射击队要从四名运动员中选拔一名运动员参加比赛,选拔赛中每名队员的平均成绩与方差s2如下表所示,如果要选择一个成绩高且发挥稳定的人参赛,则这个人应是( )
A .甲 B.乙 C.丙 D.丁
【解析】选B. ∴ 选乙或丙.
又∵ s2乙<s2丙,∴ 乙的成绩较稳定,所以应选乙参赛.
= = = =
x x 8, x x 9
甲
丁
乙
丙
,
2.果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树的产量把杨梅树划分成A,B,C,D,E五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下:
(1)补齐直方图,求a的值及相应扇形的圆心角度数;
(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果.
【解析】(1)画直方图略.
a=10,相应扇形的圆心角为:360°×10%=36°.
,由样本估计总体的思想,说明通过新技术管理的甲地块杨梅产量高于乙地块杨梅产量.
3.某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲 95 82 88 81 93 79 84 78
乙 83 92 80 95 90 80 85 75
(1)请你计算这两组数据的平均数、中位数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
1、掌握方差的定义及计算方法.
方差的定义:设有n个数据 ,方差是各数据与它们的平均数 的差的平方的平均数.用 表示.
方差的意义:方差是衡量一组数据波动大小的,量,一般地,如果一组数据的方差越大,那么该组数据的波动越大.
2、知道方差的意义.
通过本课时的学习,需要我们:
2.理解方差概念的产生和形成的过程.
1.了解方差的定义和计算公式.
3.经历探索方差的应用过程,体会数据波动中的方差的求法.
为什么说新加坡是“四季温差不大”,而北京是“四季分明”呢?
甲,乙两名同学的测试成绩统计如下:
甲
85
90
90
90
95
乙
95
85
95
85
90
问题
80
85
90
95
100
成绩(分)
⑶ 现要挑选一名同学参加竞赛,若你是老师,你认为挑选哪一名比较合适?为什么?
⑴ 请分别计算两名同学的平均成绩;
⑵ 请根据这两名同学的成绩在下图中画出折线统计图;
0
1
2
3
4
5
考试次数
挑选甲同学,因为他的成绩较稳定,且呈上升趋势.
甲
乙
甲同学成绩与平均成绩的偏差的和:
乙同学成绩与平均成绩的偏差的和:
(85-90)+(90-90)+(90-90)+(90-90)+
(95-90)=
0
(95-90)+(85-90)+(95-90)+(85-90)+
(90-90)=
0
谁的稳定性好?应用什么数据来衡量?
甲同学成绩与平均成绩的偏差的平方和:
乙同学成绩与平均成绩的偏差的平方和:
(85-90)2+(90-90)2 +(90-90)2 +(90-90)2 +(95-
90)2 =
50
(95-90)2 +(85-90)2 +(95-90)2 +(85-90)2 +(90-90)2 =
100
谁的稳定性好?应用什么数据来衡量?
上述各偏差的平方和的大小还与什么有关?
——与考试次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性.
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x )2、(x2-x )2 、… 、(xn- x )2 ,那么我们用它们的平均数,即用
想一想
s2 = [(x1-x )2+(x2-x )2 +…+(xn-x )2 ]
1
n
为了刻画一组数据波动的大小,可以采用多种方
式.统计中通常采用下面的做法:设有n个数据x1,x2,…,
xn,各数据与它们的平均数的差的平方分别是 ,我们用它们的平均数,即用 来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作S2.
(x1-x)2,(x2-x)2, … ,(x-x)2
(x1-x)2,(x2-x)2, … ,(x-x)2
n
s 2= [ (x1-x)2,(x2-x)2, … ,(x-x)2]
n
n
1
讨论:(1)数据比较分散时,方差值怎样?
(2)数据比较集中时,方差值怎样?
(3)方差的大小与数据的波动性大小有怎样的关系?
结论:方差越大,数据的波动越大;
方差越小,数据的波动越小.
【例1】 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
甲团:163 164 164 165 165 166 166 167
乙团:163 165 165 166 166 167 168 168
哪个芭蕾舞团女演员的身高更整齐?
【解析】甲、乙两团演员的平均身高分别是
1、样本方差的作用是( )
A.表示总体的平均水平 B.表示样本的平均水平
C.准确表示总体的波动大小 D.表示样本的波动大小
3、在样本方差的计算公式
数字10 表示 ,数字20表示___________.
2、样本5、6、7、8、9的方差是 .
D
2
样本平均数
样本容量
ú
?
ù
ê
?
é
-
+
-
+
-
=
)
20
(
2
+
)
20
(
2
2
)
20
(
1
2
10
1
2
s
x
n
x
x
...
4、在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学
70
95
75
95
90
英语
80
85
90
85
85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数: 都是85 方差: ①数学 110; ②英语 10
建议:英语较稳定但要提高; 数学不够稳定有待努力进步!
品种
各实验田每公顷产量(单位:吨)
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
请为农科院选择玉米种子提出你的建议.
5、农科院对甲乙两种甜玉米各用10块实验田进行试验,得到两个品种每公顷产量的两组数据:
品种
各实验田每公顷产量(单位:吨)
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
甲、乙两种甜玉米的每公顷平均产量相差不是太大,但乙种
甜玉米的产量更稳定些,所以建议选择乙种玉米种子.
1.某射击队要从四名运动员中选拔一名运动员参加比赛,选拔赛中每名队员的平均成绩与方差s2如下表所示,如果要选择一个成绩高且发挥稳定的人参赛,则这个人应是( )
A .甲 B.乙 C.丙 D.丁
【解析】选B. ∴ 选乙或丙.
又∵ s2乙<s2丙,∴ 乙的成绩较稳定,所以应选乙参赛.
= = = =
x x 8, x x 9
甲
丁
乙
丙
,
2.果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树的产量把杨梅树划分成A,B,C,D,E五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下:
(1)补齐直方图,求a的值及相应扇形的圆心角度数;
(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果.
【解析】(1)画直方图略.
a=10,相应扇形的圆心角为:360°×10%=36°.
,由样本估计总体的思想,说明通过新技术管理的甲地块杨梅产量高于乙地块杨梅产量.
3.某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲 95 82 88 81 93 79 84 78
乙 83 92 80 95 90 80 85 75
(1)请你计算这两组数据的平均数、中位数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
1、掌握方差的定义及计算方法.
方差的定义:设有n个数据 ,方差是各数据与它们的平均数 的差的平方的平均数.用 表示.
方差的意义:方差是衡量一组数据波动大小的,量,一般地,如果一组数据的方差越大,那么该组数据的波动越大.
2、知道方差的意义.
通过本课时的学习,需要我们:
