1.2.4绝对值 课件 (共18张PPT)
文档属性
| 名称 | 1.2.4绝对值 课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览






文档简介
1.2 有理数
1.2.4 绝对值
人教版 七年级上
第一章 有理数
1、求下列各数的相反数。
3.在数轴上表示相反数(0除外)的两个点位于原点的 ,且与原点的距离 。
两侧
相等
2、数轴上-3的点到原点的距离是_ _
3
复习导入
问题1:看图回答问题.
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处,它们的行驶路线相同吗?它们的行驶路程相同吗?
结论:它们的行驶路线不同,行驶路程相同.
探究新知
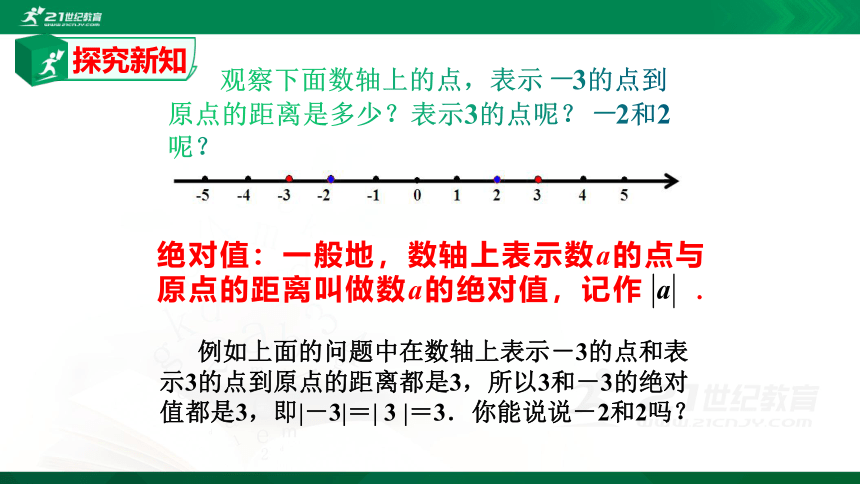
绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作 .
观察下面数轴上的点,表示-3的点到原点的距离是多少?表示3的点呢?-2和2呢?
例如上面的问题中在数轴上表示-3的点和表示3的点到原点的距离都是3,所以3和-3的绝对值都是3,即|-3|=| 3 |=3.你能说说-2和2吗?
探究新知
(1)式子∣-5.7∣表示的意思是 。
(2)—2的绝对值表示它到原点的距离是 个单位,记作 ;
即绝对值强调的是:
点到原点的距离
-5.7的绝对值
2
根据对概念的理解完成下面的问题:
探究新知
1.-2的绝对值是____,说明数轴上表示-2
的点到____的距离是____个长度单位.
2.-0.8的绝对值是____ .
3.口答:
问题2:回答下列问题
2
原点
2
0.8
6
8.2
0
3
探究新知
完成下面的题并思考问题:
∣24∣= ,∣+3.1∣= ,
∣ ∣= ,∣- ∣= ;
∣0∣= ;
问题:按行看你发现数绝对值都有什么规律?
24
3.1
6
0
-6
探究新知
由此可知绝对值的性质:
一个正数的绝对值是 ;
一个负数的绝对值是 ;
0的绝对值是 。
它本身
它的相反数
0
归纳总结
符号表示:
1)当a是正数(即a>0)时∣a∣= ;
2)当a是负数(即a<0)∣a∣= ;
3)当a=0时∣a∣= ;
a
-a
0
不论有理数a取何值,它的绝对值总是正数或0(也称非负数)。
即对任意有理数a,总有
探究新知
请回答下列问题
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
所以不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有
一个数的绝对值是指在数轴上表示这个数的点到原点的距离。
探究新知
思考下面问题:互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
归纳结论:互为相反数的两个数的绝对值相等.
零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
探究新知
1.判断并改错
(1)一个数的绝对值等于本身,则这个数一定是正数;
(2)一个数的绝对值等于它的相反数,则这个数一定
是负数;
(3)如果两个数的绝对值相等,那么这两个数一定相等;
(4)有理数的绝对值一定是非负数;
(5)两个有理数比大小,绝对值大的反而小.
非负数
非正数
相等或互为相反数
正确
两个负数比较大小,绝对值大的反而小
1、求下列各数的绝对值:
2、绝对值等于4的数是 ,
它们的关系是: 。
4和-4
互为相反数
各数的绝对值分别 为:
课堂练习
3、给出下列说法:
①互为相反数的两个数绝对值相等;
②绝对值等于本身的数只有正数;
③不相等的两个数绝对值不相等;
④绝对值相等的两数一定相等.
其中正确的有…………( )
A.0个B.1个 C.2个 D.3个
B
通过本节课学习同学们有哪些收获?
大家相互交流一下。
课堂小结
教科书习题1.2第5,6,7,8题.
作业布置
1.2.4 绝对值
人教版 七年级上
第一章 有理数
1、求下列各数的相反数。
3.在数轴上表示相反数(0除外)的两个点位于原点的 ,且与原点的距离 。
两侧
相等
2、数轴上-3的点到原点的距离是_ _
3
复习导入
问题1:看图回答问题.
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处,它们的行驶路线相同吗?它们的行驶路程相同吗?
结论:它们的行驶路线不同,行驶路程相同.
探究新知
绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作 .
观察下面数轴上的点,表示-3的点到原点的距离是多少?表示3的点呢?-2和2呢?
例如上面的问题中在数轴上表示-3的点和表示3的点到原点的距离都是3,所以3和-3的绝对值都是3,即|-3|=| 3 |=3.你能说说-2和2吗?
探究新知
(1)式子∣-5.7∣表示的意思是 。
(2)—2的绝对值表示它到原点的距离是 个单位,记作 ;
即绝对值强调的是:
点到原点的距离
-5.7的绝对值
2
根据对概念的理解完成下面的问题:
探究新知
1.-2的绝对值是____,说明数轴上表示-2
的点到____的距离是____个长度单位.
2.-0.8的绝对值是____ .
3.口答:
问题2:回答下列问题
2
原点
2
0.8
6
8.2
0
3
探究新知
完成下面的题并思考问题:
∣24∣= ,∣+3.1∣= ,
∣ ∣= ,∣- ∣= ;
∣0∣= ;
问题:按行看你发现数绝对值都有什么规律?
24
3.1
6
0
-6
探究新知
由此可知绝对值的性质:
一个正数的绝对值是 ;
一个负数的绝对值是 ;
0的绝对值是 。
它本身
它的相反数
0
归纳总结
符号表示:
1)当a是正数(即a>0)时∣a∣= ;
2)当a是负数(即a<0)∣a∣= ;
3)当a=0时∣a∣= ;
a
-a
0
不论有理数a取何值,它的绝对值总是正数或0(也称非负数)。
即对任意有理数a,总有
探究新知
请回答下列问题
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
所以不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有
一个数的绝对值是指在数轴上表示这个数的点到原点的距离。
探究新知
思考下面问题:互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
归纳结论:互为相反数的两个数的绝对值相等.
零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
探究新知
1.判断并改错
(1)一个数的绝对值等于本身,则这个数一定是正数;
(2)一个数的绝对值等于它的相反数,则这个数一定
是负数;
(3)如果两个数的绝对值相等,那么这两个数一定相等;
(4)有理数的绝对值一定是非负数;
(5)两个有理数比大小,绝对值大的反而小.
非负数
非正数
相等或互为相反数
正确
两个负数比较大小,绝对值大的反而小
1、求下列各数的绝对值:
2、绝对值等于4的数是 ,
它们的关系是: 。
4和-4
互为相反数
各数的绝对值分别 为:
课堂练习
3、给出下列说法:
①互为相反数的两个数绝对值相等;
②绝对值等于本身的数只有正数;
③不相等的两个数绝对值不相等;
④绝对值相等的两数一定相等.
其中正确的有…………( )
A.0个B.1个 C.2个 D.3个
B
通过本节课学习同学们有哪些收获?
大家相互交流一下。
课堂小结
教科书习题1.2第5,6,7,8题.
作业布置
