青岛版五四制 四年级数学下册5.3分数的基本性质 教案
文档属性
| 名称 | 青岛版五四制 四年级数学下册5.3分数的基本性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 11:13:51 | ||
图片预览


文档简介
《分数的基本性质》教学设计
教学内容:(青岛版)五四制小学数学四年级下册第五单元信息窗三
教学目标:
1.归纳、理解并掌握分数的基本性质,能初步运用分数的基本性质解决有关的数学问题。
2.经历观察、比较、猜测、验证、总结等数学活动,渗透变中有不变、数形结合和推理、极限等数学思想。
3.发展问题意识,养成会思善问的学习品质。
教学重难点:
借助素材抽象分数的基本性质,理解并掌握分数的基本性质。
评价设计:
1.通过“自主探索,构建新知”环节中“梳理归纳,思中顿悟”及“巩固拓展,提升认识”等活动来检测目标1的达成;
2.通过“猜测验证,初步感知”、“ 观察想象,深入体验”、“ 尝试表达、感悟”以及“沟通分数的基本性质与商不变规律之间的联系”等活动来检测目标2的达成;
3.通过“看了刚才这段视频,你能提出什么数学问题”、“你有什么疑问”等贯穿于课堂始终的环节检测目标3的达成。
课堂前测:
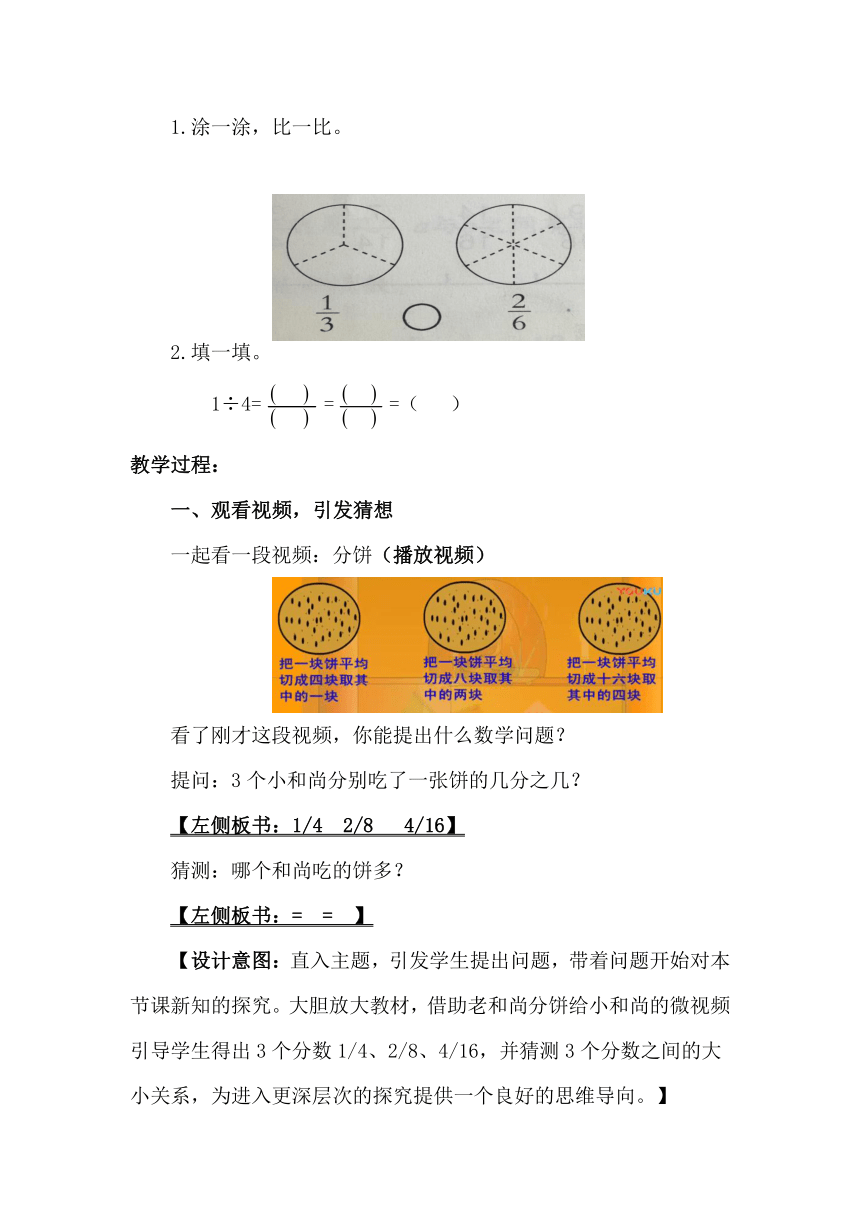
1.涂一涂,比一比。
2.填一填。
1÷4===( )
教学过程:
一、观看视频,引发猜想
一起看一段视频:分饼(播放视频)
看了刚才这段视频,你能提出什么数学问题?
提问:3个小和尚分别吃了一张饼的几分之几?
【左侧板书:1/4 2/8 4/16】
猜测:哪个和尚吃的饼多?
【左侧板书:= = 】
【设计意图:直入主题,引发学生提出问题,带着问题开始对本节课新知的探究。大胆放大教材,借助老和尚分饼给小和尚的微视频引导学生得出3个分数1/4、2/8、4/16,并猜测3个分数之间的大小关系,为进入更深层次的探究提供一个良好的思维导向。】
二、自主探索,构建新知
1.动手实践,做中感悟。
(1)猜测验证,初步感知。
1/4、2/8、4/16是不是相等的?【左板:= = ? ?】数学里面是一定要说理由的。(课件)请你想办法验证,这三个分数相等或者不相等。
(学具准备:A. 3个等圆片、3个不同大小的圆片、研究记录单;B.3个相同的长方形、3个不同大小的长方形、研究记录单;C.研究记录单。)
(课件出示学具)课前,老师已经把不同类型的验证材料分别发到了你们的桌子上。同桌合作,想一想怎样能利用这些材料来进行有效的验证。开始。
我们来交流一下,你有什么办法能说明3个分数相等或者不相等。注意说清楚你验证的过程以及结论。
<方法1:一个圆片平均分成4份,涂其中一份;另一个圆片平均分成8份,涂其中2份;第三个圆片平均分成16份,涂其中4份。3个圆片涂的部分一样大,我认为它们是相等的。>
对于这位同学的验证,你有疑问吗?
<预设:怎样确定三个圆片的阴影部分是一样大的?>
有谁验证的材料跟他是不同的?
<方法2:长方形……>
从这两组验证中,你发现了什么?
<预设:图形不同;验证方法相同;验证结论相同。>
圆片和长方形我都提供了两组,他们不约而同地选择了完全相同的一组,你们呢?对此,谁有问题要问?
画图确实是我们研究问题的一个好方法。大家看,(课件演示)一个长方形平均分成4份,涂色部分是它的——?把图中的每一份再平均分成两份,涂色部分是它的——?(把图中的每一份再平均分成两份)现在呢?
观察三个图形,什么变了?什么不变?
谁还有不同的验证方法?
<预设方法3:1/4=1÷4=0.25,2/8=2÷8=0.25,4/16=4÷16=0.25,三个算式结果是相等的,所以1/4=2/8=4/16>
我们用到的方法虽然不同,但是殊途同归,都有效验证了1/4
=2/8=4/16。 【擦掉板书?】
【设计意图:探究1/4与2/8、4/16是否相等,明确大小相等但分子、分母不同的分数确实存在,获得证明分数相等的不同方法,初步感受变中的不变。】
(2)观察想象,深入体验。
①通过刚才的操作我们可以肯定,分子、分母不同但大小相等的分数确实存在。(课件出示)那你能在表示1/3这幅图的基础上想办法变化出和1/3相等的分数吗?
(课件出示:每一份平均分成2份;3份)1/3=2/6=3/9
【板书:1/3=2/6=3/9】
②继续观察(课件出示数轴),通过这幅图你能找到一组相等的分数吗?
【板书:2/4=4/8=8/16】
想像一下,无限平分下去,能得到多少个与2/4相等的分数?(课件出示……)和1/4、1/3相等的分数呢?
由于平均分的份数越来越多,所以我们找到的分数,分子分母都比原来的大,能想一个分子分母小一点的吗?(课件出示1/2)
【2/4=4/8=8/16前板书:1/2】
对于这个答案,你有疑问吗?(课件消失小竖线)
【设计意图:层层递进,感受图中的变和不变,渗透极限思想,同时也为后面的研究积累丰富的素材。】
2.梳理归纳,思中顿悟
(1)尝试表达、感悟
①通过猜测验证、观察想象,我们找到了这样三组相等的分数。观察这三组分数,什么变了?什么不变?
【板书:分数的分子和分母 分数的大小不变】
追问:这有没有激起你心中的疑问呢?
对呀!究竟分子分母怎样变,才使得分数的大小不变呢?你可以选取其中某一组分数来进行观察研究,也可以三组分数一起对比观察,找一找这“变中不变”的奥妙所在。
小组交流
全班交流:让我们在分享中不断完善我们的发现好吗?
【板书:同时乘 相同的数】
②细心的同学可能发现了,刚才我们一直是从左往右观察,如果
换个角度,猜猜老师想问什么?
【板书:或除以】
(2)沟通分数的基本性质与商不变规律之间的联系
联系:轻声读一读。有没有感觉非常熟悉?你想到了什么?商不变规律。
(课件出示商不变的规律)
完善:刚才总结出来的结论,完整吗?可以怎么补充?
【板书:(0除外)】
揭题:分数的基本性质,这就是分数相等的奥妙所在。
用我们最自豪的姿态,大声把我们发现的规律说出来好吗?
在这句话中,你认为有哪些关键词,是我们要重点关注的?
【设计意图:放手分析三个典型例子,经历观察、推理、总结,从大量的表象抽象出规律,渗透归纳推理数学思想。通过类比,沟通与商不变规律的联系,促进学习的正迁移,着力对关键词的导学,加深对概念的理解。】
三、巩固拓展,提升认识
1.判断并说明理由。
2.填空
= = 16/40==
3.把2/3和10/24化成分母是12而大小不变的分数。
【设计意图:概念辨析与知识应用相结合,有效夯实本节课所学知识,体现训练的层次与梯度。】
四、反思评价,完善认知
通过这节课的学习你有什么收获?
我们来回顾一下走过的路。(配乐播放课件)
【设计意图:在对“有什么收获?”的回顾中,帮助学生梳理课堂学习的内容、方法,更有效地形成知识联系。】
板书设计:
分数的基本性质
1/4=2/8=4/16 分数的分子和分母同时乘
1/3=2/6=3/9 (或除以)相同的数(0除外),
1/2=2/4=4/8=8/16 分数的大小不变。
教学内容:(青岛版)五四制小学数学四年级下册第五单元信息窗三
教学目标:
1.归纳、理解并掌握分数的基本性质,能初步运用分数的基本性质解决有关的数学问题。
2.经历观察、比较、猜测、验证、总结等数学活动,渗透变中有不变、数形结合和推理、极限等数学思想。
3.发展问题意识,养成会思善问的学习品质。
教学重难点:
借助素材抽象分数的基本性质,理解并掌握分数的基本性质。
评价设计:
1.通过“自主探索,构建新知”环节中“梳理归纳,思中顿悟”及“巩固拓展,提升认识”等活动来检测目标1的达成;
2.通过“猜测验证,初步感知”、“ 观察想象,深入体验”、“ 尝试表达、感悟”以及“沟通分数的基本性质与商不变规律之间的联系”等活动来检测目标2的达成;
3.通过“看了刚才这段视频,你能提出什么数学问题”、“你有什么疑问”等贯穿于课堂始终的环节检测目标3的达成。
课堂前测:
1.涂一涂,比一比。
2.填一填。
1÷4===( )
教学过程:
一、观看视频,引发猜想
一起看一段视频:分饼(播放视频)
看了刚才这段视频,你能提出什么数学问题?
提问:3个小和尚分别吃了一张饼的几分之几?
【左侧板书:1/4 2/8 4/16】
猜测:哪个和尚吃的饼多?
【左侧板书:= = 】
【设计意图:直入主题,引发学生提出问题,带着问题开始对本节课新知的探究。大胆放大教材,借助老和尚分饼给小和尚的微视频引导学生得出3个分数1/4、2/8、4/16,并猜测3个分数之间的大小关系,为进入更深层次的探究提供一个良好的思维导向。】
二、自主探索,构建新知
1.动手实践,做中感悟。
(1)猜测验证,初步感知。
1/4、2/8、4/16是不是相等的?【左板:= = ? ?】数学里面是一定要说理由的。(课件)请你想办法验证,这三个分数相等或者不相等。
(学具准备:A. 3个等圆片、3个不同大小的圆片、研究记录单;B.3个相同的长方形、3个不同大小的长方形、研究记录单;C.研究记录单。)
(课件出示学具)课前,老师已经把不同类型的验证材料分别发到了你们的桌子上。同桌合作,想一想怎样能利用这些材料来进行有效的验证。开始。
我们来交流一下,你有什么办法能说明3个分数相等或者不相等。注意说清楚你验证的过程以及结论。
<方法1:一个圆片平均分成4份,涂其中一份;另一个圆片平均分成8份,涂其中2份;第三个圆片平均分成16份,涂其中4份。3个圆片涂的部分一样大,我认为它们是相等的。>
对于这位同学的验证,你有疑问吗?
<预设:怎样确定三个圆片的阴影部分是一样大的?>
有谁验证的材料跟他是不同的?
<方法2:长方形……>
从这两组验证中,你发现了什么?
<预设:图形不同;验证方法相同;验证结论相同。>
圆片和长方形我都提供了两组,他们不约而同地选择了完全相同的一组,你们呢?对此,谁有问题要问?
画图确实是我们研究问题的一个好方法。大家看,(课件演示)一个长方形平均分成4份,涂色部分是它的——?把图中的每一份再平均分成两份,涂色部分是它的——?(把图中的每一份再平均分成两份)现在呢?
观察三个图形,什么变了?什么不变?
谁还有不同的验证方法?
<预设方法3:1/4=1÷4=0.25,2/8=2÷8=0.25,4/16=4÷16=0.25,三个算式结果是相等的,所以1/4=2/8=4/16>
我们用到的方法虽然不同,但是殊途同归,都有效验证了1/4
=2/8=4/16。 【擦掉板书?】
【设计意图:探究1/4与2/8、4/16是否相等,明确大小相等但分子、分母不同的分数确实存在,获得证明分数相等的不同方法,初步感受变中的不变。】
(2)观察想象,深入体验。
①通过刚才的操作我们可以肯定,分子、分母不同但大小相等的分数确实存在。(课件出示)那你能在表示1/3这幅图的基础上想办法变化出和1/3相等的分数吗?
(课件出示:每一份平均分成2份;3份)1/3=2/6=3/9
【板书:1/3=2/6=3/9】
②继续观察(课件出示数轴),通过这幅图你能找到一组相等的分数吗?
【板书:2/4=4/8=8/16】
想像一下,无限平分下去,能得到多少个与2/4相等的分数?(课件出示……)和1/4、1/3相等的分数呢?
由于平均分的份数越来越多,所以我们找到的分数,分子分母都比原来的大,能想一个分子分母小一点的吗?(课件出示1/2)
【2/4=4/8=8/16前板书:1/2】
对于这个答案,你有疑问吗?(课件消失小竖线)
【设计意图:层层递进,感受图中的变和不变,渗透极限思想,同时也为后面的研究积累丰富的素材。】
2.梳理归纳,思中顿悟
(1)尝试表达、感悟
①通过猜测验证、观察想象,我们找到了这样三组相等的分数。观察这三组分数,什么变了?什么不变?
【板书:分数的分子和分母 分数的大小不变】
追问:这有没有激起你心中的疑问呢?
对呀!究竟分子分母怎样变,才使得分数的大小不变呢?你可以选取其中某一组分数来进行观察研究,也可以三组分数一起对比观察,找一找这“变中不变”的奥妙所在。
小组交流
全班交流:让我们在分享中不断完善我们的发现好吗?
【板书:同时乘 相同的数】
②细心的同学可能发现了,刚才我们一直是从左往右观察,如果
换个角度,猜猜老师想问什么?
【板书:或除以】
(2)沟通分数的基本性质与商不变规律之间的联系
联系:轻声读一读。有没有感觉非常熟悉?你想到了什么?商不变规律。
(课件出示商不变的规律)
完善:刚才总结出来的结论,完整吗?可以怎么补充?
【板书:(0除外)】
揭题:分数的基本性质,这就是分数相等的奥妙所在。
用我们最自豪的姿态,大声把我们发现的规律说出来好吗?
在这句话中,你认为有哪些关键词,是我们要重点关注的?
【设计意图:放手分析三个典型例子,经历观察、推理、总结,从大量的表象抽象出规律,渗透归纳推理数学思想。通过类比,沟通与商不变规律的联系,促进学习的正迁移,着力对关键词的导学,加深对概念的理解。】
三、巩固拓展,提升认识
1.判断并说明理由。
2.填空
= = 16/40==
3.把2/3和10/24化成分母是12而大小不变的分数。
【设计意图:概念辨析与知识应用相结合,有效夯实本节课所学知识,体现训练的层次与梯度。】
四、反思评价,完善认知
通过这节课的学习你有什么收获?
我们来回顾一下走过的路。(配乐播放课件)
【设计意图:在对“有什么收获?”的回顾中,帮助学生梳理课堂学习的内容、方法,更有效地形成知识联系。】
板书设计:
分数的基本性质
1/4=2/8=4/16 分数的分子和分母同时乘
1/3=2/6=3/9 (或除以)相同的数(0除外),
1/2=2/4=4/8=8/16 分数的大小不变。
