一元一次方程复习

(共18张PPT)
第四章
一元一次方程的复习（一）
1、什么是一元一次方程
（1）方程的两边都是整式（分母中不含未知数）
（2）只含有一个未知数
（3）未知数的指数是一次.
挑战记忆
练习：1.判断下列各式中哪些是一元一次方程？
（1） 5x=0 （2）1+3x （3）y =4+y
（4）x+y=5 （5） （6） 3m+2=1–m
×
√
×
×
×
√
2.同步学习95页 自我尝试1
1、若x=2是方程ax+3=2x解，则a=_____
2 .(2009 ·安顺)已知关于x的方程4x-3m=2的解是x=m，则m的值是__。
-2
2.方程的解：
使方程左右两边相等的未知数的值
练习：
方法点拨：把解代入方程
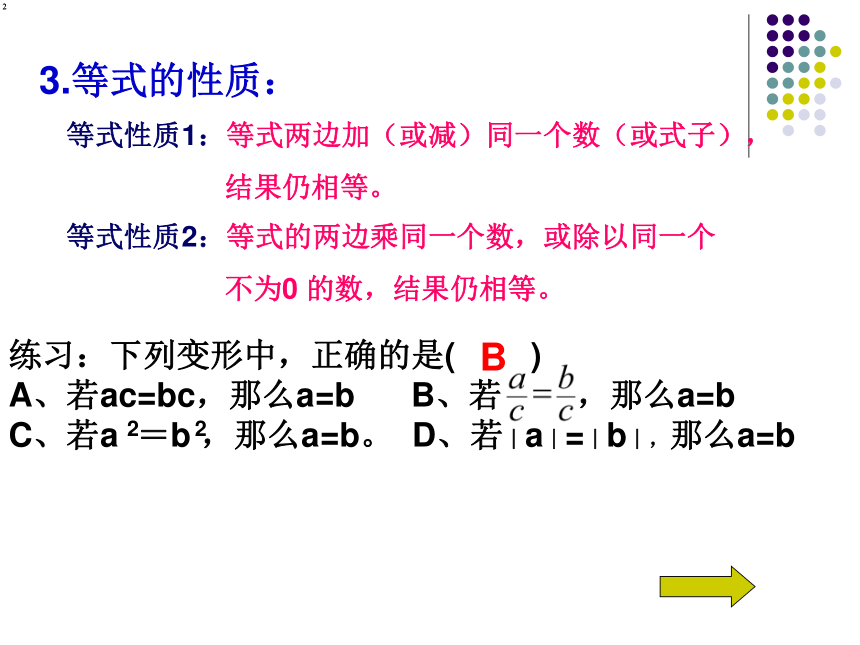
3.等式的性质：
等式性质1：等式两边加（或减）同一个数（或式子），
结果仍相等。
等式性质2：等式的两边乘同一个数，或除以同一个
不为0 的数，结果仍相等。
练习：下列变形中，正确的是( )
A、若ac=bc，那么a=b B、若 ，那么a=b
C、若a ＝b ，那么a=b。 D、若︱a︱=︱b︱，那么a=b
2
2
B
（1）去分母：
不要漏乘不含分母的项
（2）去括号：
去括号后的符号变化,并且不要漏乘括号中的每一项
例：去括号
A、+（2X- 5)= ___________ B、- (2X- 5)=__________
C、3（3X+1)=___________ D、-2(3X- 5)= _________
（3）移项：
移动的项要变号
例：方程3X+20=4X-25+5
移项正确的是：A、3X--4X=-5-25-20
B、 3X-4X=-25+5-20
4、解一元一次方程的一般步骤
3(3Y-1)-12=2(5Y-7)
2X- 5
- 2X+5
9X+3
- 6X+10
√
×
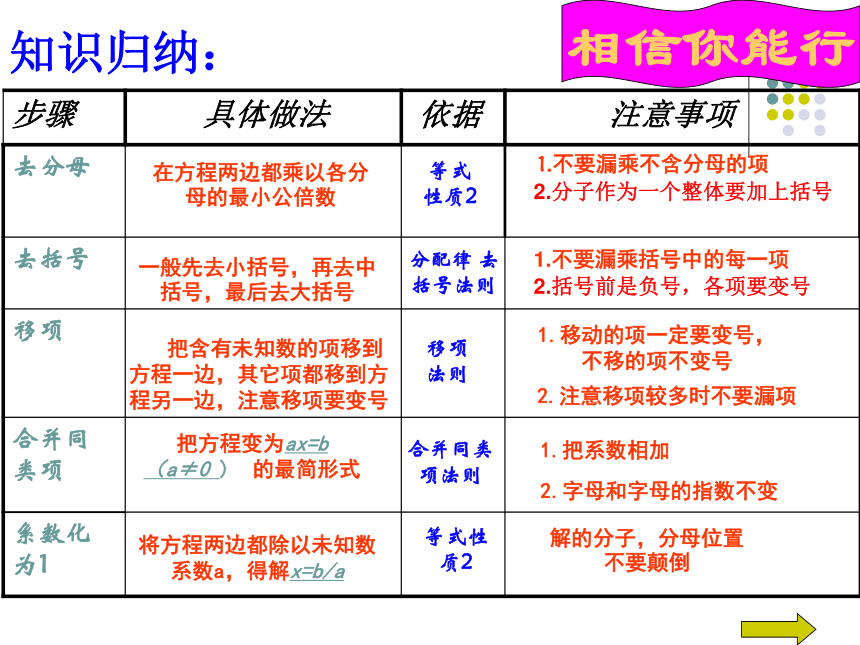
步骤 具体做法 依据 注意事项
去分母
去括号
移项
合并同类项
系数化为1
在方程两边都乘以各分母的最小公倍数
等式
性质2
1.不要漏乘不含分母的项
一般先去小括号，再去中括号，最后去大括号
分配律 去括号法则
1.不要漏乘括号中的每一项
把含有未知数的项移到方程一边，其它项都移到方程另一边，注意移项要变号
移项
法则
1.移动的项一定要变号，
不移的项不变号
2.注意移项较多时不要漏项
把方程变为ax=b
（a≠0 ) 的最简形式
合并同类项法则
2.字母和字母的指数不变
将方程两边都除以未知数系数a，得解x=b/a
等式性质2
解的分子，分母位置不要颠倒
1.把系数相加
相信你能行
2.分子作为一个整体要加上括号
知识归纳：
2.括号前是负号，各项要变号
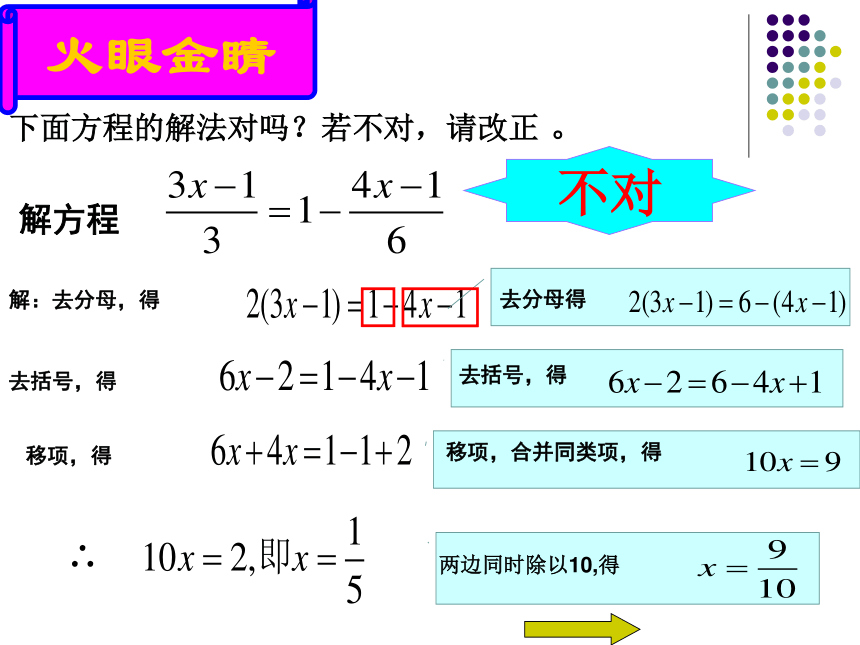
解方程
解：去分母，得
去括号，得
移项，得
∴
去分母得
去括号，得
移项，合并同类项，得
下面方程的解法对吗？若不对，请改正 。
不对
两边同时除以10,得
火眼金睛
例：解下列方程：
解：原方程可化为：
注意:如果分母不是整数的方程可以应用分数的基本性质转化成整数，这样有利于去分母。
去分母, 得5x –（1.5 - x）= 1
去括号，得 5x – 1.5 + x = 1
移项, 得 5x + x = 1 + 1.5
合并同类项,得 6x= 2.5
两边同除以6, 得x=
6.小明同学解方程 ，由于在去分母
时，将方程右边的项 -1 忘记乘3，结果错求得方程的解为x=2。你能求出原题中a的值吗？并求出原方程正确的解。
考查目标③ 解一元一次方程
考查目标4 （方程的简单应用）
（1）若 。
（2）若 是同类项，则2m-3n= 。
（3）代数式x+6与3(x+2)的值互为相反数，则x的值为 。
（4）若 与 互为倒数，则x= 。
-3
-4
-1.5
-3
列方程解应用题的一般步骤有：
⑴审题：理解题意，弄清已知量、未知量以及题目给 出或涉及的基本等量关系是什么；
⑵设未知数：直接或间接设元
⑶用含未知数的代数式表示各个相关量；
⑷据等量关系列方程；
⑸解方程；
⑹检验写答。
10 月 18 日 是小新妈妈的生日，于是一早小新爸爸让小新去买一些生日蜡烛。
(1)已知小新与妈妈的年龄和是55岁，妈妈的年龄又比小新的年龄的3倍小5岁，那么小新得买多少根蜡烛才刚刚好呢？
分析：妈妈的年龄+小新的年龄=55岁
妈妈的年龄=小新的年龄×3 - 5
解：设妈妈的年龄为x岁，那么小新的 年龄为（55- x）岁，根据题意得，
X= 3（55- x）- 5
解得 x=40
答：小新得买40根蜡烛才刚刚好。
妈妈过生日，小新准备去银行拿出自己的压岁钱给妈妈买一份礼物。
(2) 小新的压岁钱已存了1年，已知银行的年利率为1.4%，这次小新共拿出202.8元，你能知道小新存入的压岁钱是多少吗？
那么小新存入1年后可拿出(x+1.4%x)元，
解：设小新存入压岁钱为x元
x+1.4%x = 202.8
解得，x = 200
分析：本息和=本金+利息
答：小新存入压岁钱为200元。
来到商场，小新决定给妈妈买一件她最喜爱的毛衣.
(3)商场正在搞活动，为了吸引消费者，商场将进价为80元的毛衣按标价8折销售，仍可获20元的利润，你知道小新买毛衣用了多少钱吗？
分析：售价-进价=利润
标价× 打折数=售价
解：设毛衣的标价为x元，根据题意得，
80%x=80+20
解得，x=125
答：毛衣的标价为125元。
你能说出毛衣的标价吗？
回到家，小新心想糟糕：生日蜡烛，后又想妈妈平时最喜欢喝红酒了，就顺道买两瓶红酒吧！于是他兴冲冲地出门去了。
(4)到家后，爸爸问起红酒多少钱一瓶时，小新愣住了，买酒时忘问了，他只记得：蜡烛是0.2元/支，共用去八元钱，口袋里还剩下40.8元，你能帮助小新说出红酒每瓶的价格吗？
100元
8元
202.8元
还剩40.8 元
解：设红酒每瓶x元，根据题意得，
2x
100+8+2x+40.8=202.8
解得， x=27
答：红酒每瓶27元。
一会儿，爸爸做饭去了，到十一点了，妈妈下班了，小新于是立即骑车找妈妈去了。
(5)妈妈的工厂距离小新家3千米，已知小新骑车的速度是4千米/时，妈妈骑车的速度是6千米/时，他们在途中相遇需要多长时间呢？
析：小新与妈妈相遇的时间=他们相遇后回来的时间
解：设他们相遇需要x小时,根据题意的得，
4x+6x = 3
解得 x = 0.3
0.3 ×2 = 0.6
相遇后妈妈和小新立即又以4千米/时速度一起回家，请问他们到家时已经几点了？
小新家
工厂
3千米