北师大版数学八年级下册 2.1 不等关系 课件(14张)
文档属性
| 名称 | 北师大版数学八年级下册 2.1 不等关系 课件(14张) |  | |
| 格式 | pptx | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 23:14:39 | ||
图片预览








文档简介
第二章 一元一次不等式与一元一次不等式组
1 不等关系
不等式的定义
用不等式表示数量关系 .(重点、难点)
学习目标
新课导入
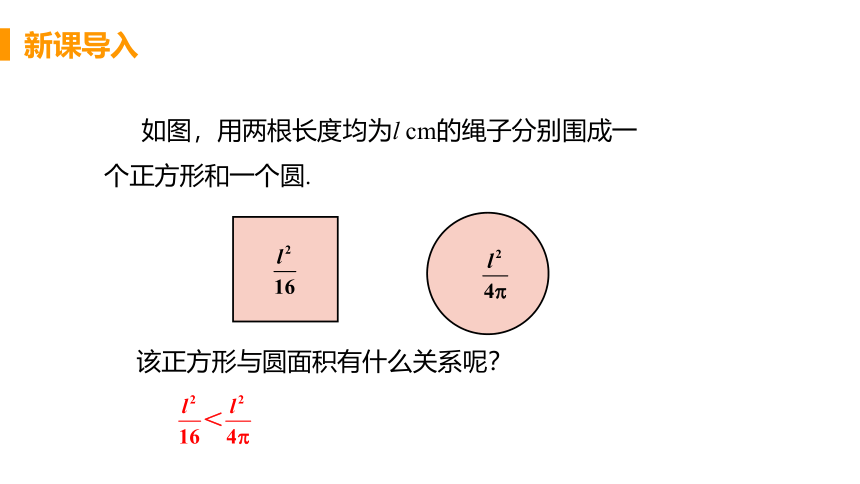
如图,用两根长度均为l cm的绳子分别围成一
个正方形和一个圆.
该正方形与圆面积有什么关系呢?
新课讲解
知识点1 不等式的定义
一般地,用符号“<”(或“≤”),“>”
(或“≥”)连接的式子叫做不等式.
新课讲解
不等式的分类(按条件分):
(1)绝对不等式:任何条件下都成立的不等式,如
a2+1>0;
(2)矛盾不等式:任何条件下都不成立的不等式,如
a2+1<0;
(3)条件不等式:在一定条件下才能成立的不等式
(主要研究的不等式).
新课讲解
4.圆锥的有关计算公式:
圆锥的高h,底面半径r,母线l的关系式:h2+r2=l2
(已知其中任意两个量,可以求出第三个量).
5. 易错警示:圆锥的母线长为圆锥侧面展开后所得 扇
形的半径,要注意与圆锥底面半径相区分.
新课讲解
例
典例分析
判断一个式子是否为不等式的关键是看式子中是
否含有“≠”“>”“<”“≥”“≤”;因此
②③⑤⑥⑧是不等式.
分析:
下列式子是不等式的>有( )
①2x=20;②3>2;③x≠4-3;④5a+6b;
A.2个 B.3个 C.4个 D.5个
D
新课讲解
例
典例分析
(1)a2表示非负数,∴a2≥0.
(2)|x|≥0,|y|≥0,∴|x|+|y|≥|x+y|.
(3)不小于就是大于或等于.
(4)当a是负数或0时,|a|=-a.
分析:
用不等号填空.
(1)a2____0;(2)|x|+|y|____|x+y|;
(3)若a不小于1,则a____1;
(4)当a____0时,|a|=-a.
≥
≥
≥
≤
新课讲解
练一练
1 用“<”或“>”号填空.
(1)-2____2; (2)-3____-2;
(3)12____6; (4)0____-8;
(5)-a____a (a>0); (6)-a____a(a<0).
2 下列数学表达式:
①-2<0;②4x+2y>0;③x=1;④x2-xy;
⑤x≠3;⑥x-1<y+2.其中不等式有( )
A.5个 B.4个 C.3个 D.2个
<
<
>
>
<
>
B
新课讲解
知识点2 用不等式表示数量关系
1. 列不等式就是用不等式表示代数式之间的不等关系.
2. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
新课讲解
例
典例分析
(1)中“正数”用“>0”表示;
(3)中“非正数”即负数或0,用“≤0”表示;
(4)中“不大于”即“小于或等于”,用“≤”表示.
分析:
列不等式:
(1)a与1的和是正数:________;
(2)y的2倍与1的和大于3:________;
(3)x的一半与x的2倍的和是非正数:__________;
(4)c与4的和不大于-2:________.
a+1>0
2y+1>3
c+4≤-2
新课讲解
列不等式首先要找出表示不等关系的关键词,然后用
表示数量关系的式子表示不等式的左边和右边;
常用不等关系的基本语言的意义:
(1)a是正数等价于a>0; (2)a是负数等价于a<0;
(3)a是非正数等价于a≤0; (4)a是非负数等价于a≥0;
(5)a大于b等价于a-b>0; (6)a小于b等价于a-b<0;
(7)a不大于b等价于a≤b; (8)a不小于b等价于a≥b;
(9)a,b同号等价于ab>0或 >0;
(10)a,b异号等价于ab<0或 <0.,
新课讲解
例
典例分析
总收入是甲种蔬菜的收入加上乙种蔬菜的收入,不
低于是大于或等于.
分析:
有10位菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若使总收入不低于15.6万元,试写出安排甲种蔬菜的种植人数x应满足的不等式.
安排x人种甲种蔬菜,那么有(10-x)人种乙种蔬菜,
则0.5×3x+0.8×2×(10-x)≥15.6.
解:
新课讲解
例
典例分析
0.3x+0.5y≤8表示x的0.3倍与y的0.5倍的和小于
或等于8.
分析:
设计实际背景表示不等式:0.3x+0.5y≤8.
(答案不唯一)
如:某商店每本练习本是0.5元,每支铅笔是
0.3元,小明带了8元钱,购买了x支铅笔和y本
练习本,则它们的数量关系为:0.3x+0.5y≤8.
解:
新课讲解
练一练
用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
解:(1)a≥0. (2)c>a,c>b.
(3)x+17<5x. (4)x2+y2≥2xy.
课堂小结
1.一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式.
2. 列不等式就是用不等式表示代数式之间的不等关系.
3. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
当堂小练
1.用不等式表示“x的2倍与5的差是负数”正确
的是( )
A.2x-5>0 B.2x-5<0
C.2x-5≠0 D.2x-5≤0
B
当堂小练
2.如图,A,B两点在数轴上表示的数分别为a,b,下列式子成立的是( )
A.ab>0 B.a+b<0
C.(b-1)(a+1)>0 D.(b-1)(a-1)>0
C
拓展与延伸
某市的最高气温是33 ℃,最低气温是24 ℃,则该市的
气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
D
布置作业
请完成对应习题
1 不等关系
不等式的定义
用不等式表示数量关系 .(重点、难点)
学习目标
新课导入
如图,用两根长度均为l cm的绳子分别围成一
个正方形和一个圆.
该正方形与圆面积有什么关系呢?
新课讲解
知识点1 不等式的定义
一般地,用符号“<”(或“≤”),“>”
(或“≥”)连接的式子叫做不等式.
新课讲解
不等式的分类(按条件分):
(1)绝对不等式:任何条件下都成立的不等式,如
a2+1>0;
(2)矛盾不等式:任何条件下都不成立的不等式,如
a2+1<0;
(3)条件不等式:在一定条件下才能成立的不等式
(主要研究的不等式).
新课讲解
4.圆锥的有关计算公式:
圆锥的高h,底面半径r,母线l的关系式:h2+r2=l2
(已知其中任意两个量,可以求出第三个量).
5. 易错警示:圆锥的母线长为圆锥侧面展开后所得 扇
形的半径,要注意与圆锥底面半径相区分.
新课讲解
例
典例分析
判断一个式子是否为不等式的关键是看式子中是
否含有“≠”“>”“<”“≥”“≤”;因此
②③⑤⑥⑧是不等式.
分析:
下列式子是不等式的>有( )
①2x=20;②3>2;③x≠4-3;④5a+6b;
A.2个 B.3个 C.4个 D.5个
D
新课讲解
例
典例分析
(1)a2表示非负数,∴a2≥0.
(2)|x|≥0,|y|≥0,∴|x|+|y|≥|x+y|.
(3)不小于就是大于或等于.
(4)当a是负数或0时,|a|=-a.
分析:
用不等号填空.
(1)a2____0;(2)|x|+|y|____|x+y|;
(3)若a不小于1,则a____1;
(4)当a____0时,|a|=-a.
≥
≥
≥
≤
新课讲解
练一练
1 用“<”或“>”号填空.
(1)-2____2; (2)-3____-2;
(3)12____6; (4)0____-8;
(5)-a____a (a>0); (6)-a____a(a<0).
2 下列数学表达式:
①-2<0;②4x+2y>0;③x=1;④x2-xy;
⑤x≠3;⑥x-1<y+2.其中不等式有( )
A.5个 B.4个 C.3个 D.2个
<
<
>
>
<
>
B
新课讲解
知识点2 用不等式表示数量关系
1. 列不等式就是用不等式表示代数式之间的不等关系.
2. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
新课讲解
例
典例分析
(1)中“正数”用“>0”表示;
(3)中“非正数”即负数或0,用“≤0”表示;
(4)中“不大于”即“小于或等于”,用“≤”表示.
分析:
列不等式:
(1)a与1的和是正数:________;
(2)y的2倍与1的和大于3:________;
(3)x的一半与x的2倍的和是非正数:__________;
(4)c与4的和不大于-2:________.
a+1>0
2y+1>3
c+4≤-2
新课讲解
列不等式首先要找出表示不等关系的关键词,然后用
表示数量关系的式子表示不等式的左边和右边;
常用不等关系的基本语言的意义:
(1)a是正数等价于a>0; (2)a是负数等价于a<0;
(3)a是非正数等价于a≤0; (4)a是非负数等价于a≥0;
(5)a大于b等价于a-b>0; (6)a小于b等价于a-b<0;
(7)a不大于b等价于a≤b; (8)a不小于b等价于a≥b;
(9)a,b同号等价于ab>0或 >0;
(10)a,b异号等价于ab<0或 <0.,
新课讲解
例
典例分析
总收入是甲种蔬菜的收入加上乙种蔬菜的收入,不
低于是大于或等于.
分析:
有10位菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若使总收入不低于15.6万元,试写出安排甲种蔬菜的种植人数x应满足的不等式.
安排x人种甲种蔬菜,那么有(10-x)人种乙种蔬菜,
则0.5×3x+0.8×2×(10-x)≥15.6.
解:
新课讲解
例
典例分析
0.3x+0.5y≤8表示x的0.3倍与y的0.5倍的和小于
或等于8.
分析:
设计实际背景表示不等式:0.3x+0.5y≤8.
(答案不唯一)
如:某商店每本练习本是0.5元,每支铅笔是
0.3元,小明带了8元钱,购买了x支铅笔和y本
练习本,则它们的数量关系为:0.3x+0.5y≤8.
解:
新课讲解
练一练
用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
解:(1)a≥0. (2)c>a,c>b.
(3)x+17<5x. (4)x2+y2≥2xy.
课堂小结
1.一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式.
2. 列不等式就是用不等式表示代数式之间的不等关系.
3. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
当堂小练
1.用不等式表示“x的2倍与5的差是负数”正确
的是( )
A.2x-5>0 B.2x-5<0
C.2x-5≠0 D.2x-5≤0
B
当堂小练
2.如图,A,B两点在数轴上表示的数分别为a,b,下列式子成立的是( )
A.ab>0 B.a+b<0
C.(b-1)(a+1)>0 D.(b-1)(a-1)>0
C
拓展与延伸
某市的最高气温是33 ℃,最低气温是24 ℃,则该市的
气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
D
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
