冀教版初中数学八年级上册 16.2 线段垂直平分线性质定理 教案
文档属性
| 名称 | 冀教版初中数学八年级上册 16.2 线段垂直平分线性质定理 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 58.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 12:08:51 | ||
图片预览

文档简介
线段的垂直平分线(第一课时)
教学目标
知识与技能:
理解线段垂直平分线的性质定理。
能灵活运用垂直平分线的性质定理解决实际问题。
通过经历线段垂直平分线的性质定理的证明过程,体验逻辑推理的数学方法。
通过认识上的升华,使学生发现数学与生活的密切联系
重点:线段垂直平分线的性质定理
难点:灵活运用线段垂直平分线的性质定理解决问题
教学设计:
复习导入
如图,下列哪些图形是轴对称图形?请把对称轴画出来。
设计意图:通过动手画图,让学生回忆旧知识,激发学生的参与热情。
你能用折纸的方法验证你对上题的画法吗?
设计意图:层层设问,不断给学生设置障碍,挑起他们的热情。
讲授新课
自主探究:
如图:直线l垂直平分线段AB,P1
、P2
、P3.....是L上的点,请猜想P1
、P2
、P3.....到点A到点B的距离之间的数量关系。
猜想:用不同的方法验证你的结论
学生:小组讨论(折叠、测量、逻辑推理)
动手操作:量一量PA、PB的长。
说明:学生在画图的时候,教师走到学生当中巡视,及时纠错、
表扬。
由学生归纳成命题,教师给予纠正,使之规范。
师总结:线段垂直平分线上的点到线段两端的距离相等。
验证结论:
师:分析定理的条件和结论。
点P在线段AB的垂直平分线上---------PA=PB
(条件)
(结论)
师:引导学生分析,证明,写出已知,求证
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在l上。
求证:PA=PB
(由学生独立完成证明过程)
师:巡视指导后,全班讲评。
证明:∵ l⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=PB.
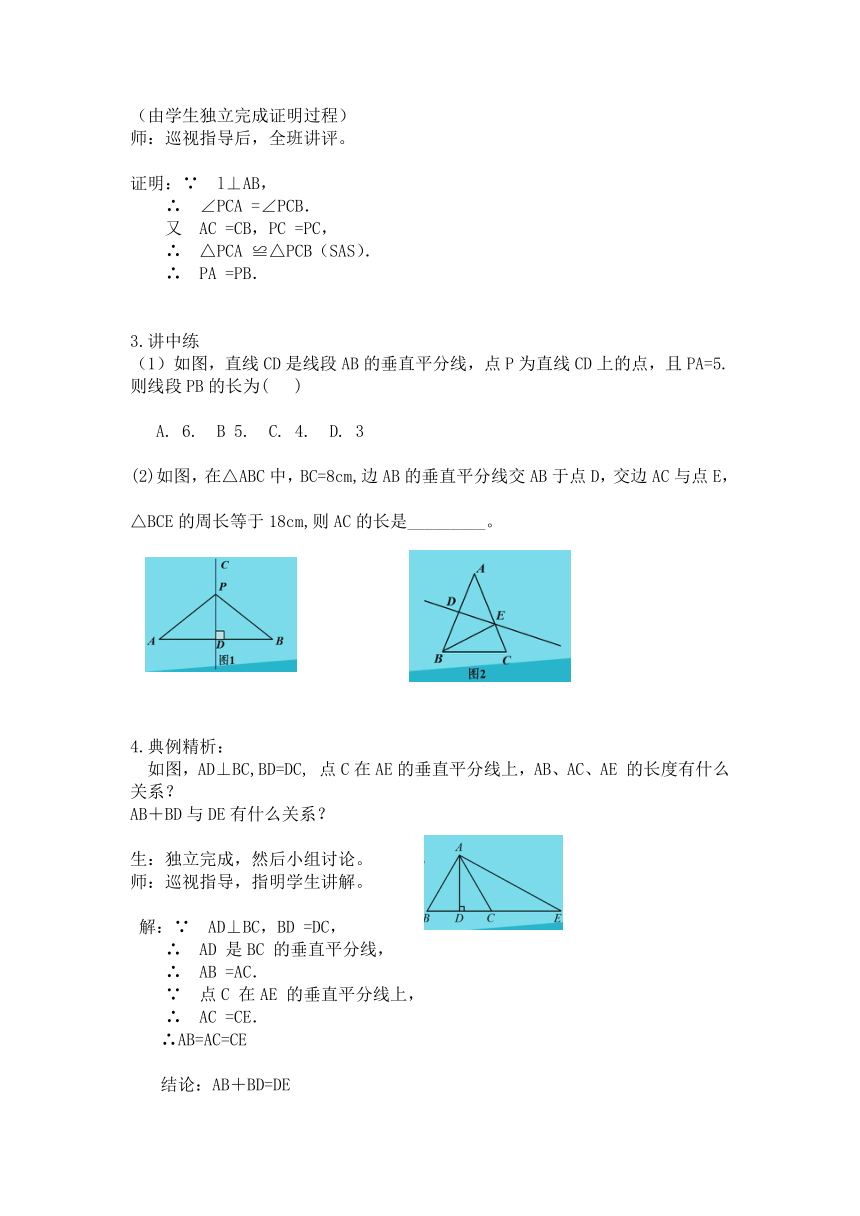
讲中练
如图,直线CD是线段AB的垂直平分线,点P为直线CD上的点,且PA=5.则线段PB的长为(
)
A.
6.
B
5.
C.
4.
D.
3
(2)如图,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC与点E,
△BCE的周长等于18cm,则AC的长是_________。
典例精析:
如图,AD⊥BC,BD=DC,
点C在AE的垂直平分线上,AB、AC、AE
的长度有什么关系?
AB+BD与DE有什么关系?
生:独立完成,然后小组讨论。
师:巡视指导,指明学生讲解。
解:∵ AD⊥BC,BD
=DC,
∴ AD
是BC
的垂直平分线,
∴ AB
=AC.
∵ 点C
在AE
的垂直平分线上,
∴ AC
=CE.
∴AB=AC=CE
结论:AB+BD=DE
三、线段垂直平分线性质定理的应用
1.问题。
已知:如图,点A,B是直线l外任意两点,在直线l上,试确定一点P,使得AP+BP最短.
生:小组探究。指明板演
师:教师巡视,并指导纠正。鼓励学习困难的学生。
解:作点A关于直线l的对称点A',
连接A'B
,交直线l于点P,则AP+BP最短.
“两点之间,线段最短”的应用。
典例精析
2.实际应用
如图,已知牧马人营地在M处,每天牧马人要先赶马群到河边饮水,再到草地上吃草,最后回到营地,试着设计出最短的牧马路线?
生:学生思考并讨论
师:
帮助学生分析,这道题很有难度。让学生体会“两点之间,
线段最短”在现实中的应用。
巩固提高
1.如图,AB是CD的垂直平分线,若AD=1.6cm,BC=2.3cm,则四边形ADBC的周长是
(
)
A.3.9cm
B.7.8cm
C.4cm
D.4.6cm
2.已知:如图,D.E分别是AB,AC的中点,CD⊥AB于点D,BE⊥AC于点E.
求证:AC=AB
五、课堂小结
通过本节课的学习,你有那些新的收获?
你学习到哪些新的知识?
你认为你本节课的表现如何?
你还有哪些困惑?
六、布置作业
习题:A组、B组
教学目标
知识与技能:
理解线段垂直平分线的性质定理。
能灵活运用垂直平分线的性质定理解决实际问题。
通过经历线段垂直平分线的性质定理的证明过程,体验逻辑推理的数学方法。
通过认识上的升华,使学生发现数学与生活的密切联系
重点:线段垂直平分线的性质定理
难点:灵活运用线段垂直平分线的性质定理解决问题
教学设计:
复习导入
如图,下列哪些图形是轴对称图形?请把对称轴画出来。
设计意图:通过动手画图,让学生回忆旧知识,激发学生的参与热情。
你能用折纸的方法验证你对上题的画法吗?
设计意图:层层设问,不断给学生设置障碍,挑起他们的热情。
讲授新课
自主探究:
如图:直线l垂直平分线段AB,P1
、P2
、P3.....是L上的点,请猜想P1
、P2
、P3.....到点A到点B的距离之间的数量关系。
猜想:用不同的方法验证你的结论
学生:小组讨论(折叠、测量、逻辑推理)
动手操作:量一量PA、PB的长。
说明:学生在画图的时候,教师走到学生当中巡视,及时纠错、
表扬。
由学生归纳成命题,教师给予纠正,使之规范。
师总结:线段垂直平分线上的点到线段两端的距离相等。
验证结论:
师:分析定理的条件和结论。
点P在线段AB的垂直平分线上---------PA=PB
(条件)
(结论)
师:引导学生分析,证明,写出已知,求证
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在l上。
求证:PA=PB
(由学生独立完成证明过程)
师:巡视指导后,全班讲评。
证明:∵ l⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=PB.
讲中练
如图,直线CD是线段AB的垂直平分线,点P为直线CD上的点,且PA=5.则线段PB的长为(
)
A.
6.
B
5.
C.
4.
D.
3
(2)如图,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC与点E,
△BCE的周长等于18cm,则AC的长是_________。
典例精析:
如图,AD⊥BC,BD=DC,
点C在AE的垂直平分线上,AB、AC、AE
的长度有什么关系?
AB+BD与DE有什么关系?
生:独立完成,然后小组讨论。
师:巡视指导,指明学生讲解。
解:∵ AD⊥BC,BD
=DC,
∴ AD
是BC
的垂直平分线,
∴ AB
=AC.
∵ 点C
在AE
的垂直平分线上,
∴ AC
=CE.
∴AB=AC=CE
结论:AB+BD=DE
三、线段垂直平分线性质定理的应用
1.问题。
已知:如图,点A,B是直线l外任意两点,在直线l上,试确定一点P,使得AP+BP最短.
生:小组探究。指明板演
师:教师巡视,并指导纠正。鼓励学习困难的学生。
解:作点A关于直线l的对称点A',
连接A'B
,交直线l于点P,则AP+BP最短.
“两点之间,线段最短”的应用。
典例精析
2.实际应用
如图,已知牧马人营地在M处,每天牧马人要先赶马群到河边饮水,再到草地上吃草,最后回到营地,试着设计出最短的牧马路线?
生:学生思考并讨论
师:
帮助学生分析,这道题很有难度。让学生体会“两点之间,
线段最短”在现实中的应用。
巩固提高
1.如图,AB是CD的垂直平分线,若AD=1.6cm,BC=2.3cm,则四边形ADBC的周长是
(
)
A.3.9cm
B.7.8cm
C.4cm
D.4.6cm
2.已知:如图,D.E分别是AB,AC的中点,CD⊥AB于点D,BE⊥AC于点E.
求证:AC=AB
五、课堂小结
通过本节课的学习,你有那些新的收获?
你学习到哪些新的知识?
你认为你本节课的表现如何?
你还有哪些困惑?
六、布置作业
习题:A组、B组
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
