冀教版初中数学八年级上册 17.1 等腰三角形 教案
文档属性
| 名称 | 冀教版初中数学八年级上册 17.1 等腰三角形 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 12:13:24 | ||
图片预览



文档简介
等腰三角形教学设计
教学目标
(一)知识与技能
1.了解等腰三角形和等边三角形相关概念
2.知道等腰三角形是轴对称图形,能利用轴对称图形的性质探索并证明等腰三角形和等边三角形的性质进行
3.能运用等腰三角形的性质进行推理和计算
(二)过程与方法
1.在等腰三角形性质的应用过程中提高学生的合情推理和演绎推理能力,培养学生观察猜想,合作探究的能力
2.体会方程思想在几何计算问题中的渗透与应用
(三)情感态度
通过学生的动手操作,合作探究激发学生解决问题的热情和团结协作的能力
教学重难点
教学重点
用等腰三角形性质定理去解决相关问题
教学难点
在等腰三角形性质的应用过程中提高学生学生的推理能力
学情分析
八年级学生观察操作猜想能力较强,但思维的灵活性不够,自主探究与合作能力也需要在课堂上逐步引导,前面学生已经学习了轴对称的性质,应引导学生用轴对称的性质去猜想等腰三角形的相关性质
教学方法
观察法,发现法,动手操作法,多媒体演示,合作探究法
教学过程
(一)创设情境,引入课题
在学生观察生活中的一些图片时,问:
1.这些图片中抽象出的平面几何图形(如房屋的钢梁架、红领巾、交通标志的外沿形状等),它们有什么共同特点?
2.你能根据这个共同特点给等腰三角形下定义吗?
有两边相等的三角形叫做等腰三角形.
介绍在等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
如图,在△ABC中,AB
=
AC.AB和
AC是腰,BC是底边,∠A是顶角,∠B和∠C是底角,
顶角是直角的等腰三角形叫做等腰直角三角形.
探索新知,渐进升华
1.动手操作,观察猜想
你能利用一张长方形的纸片和工具,借助折纸的方法剪出一个等腰三角形吗?动手做一做(要求学生课前完成)
观察所剪的三角形,思考下面的问题
(1)如图,你认为等腰△ABC是轴对称图形吗?
如果是,对称轴是哪条直线?
根据你的观察,说一说图中有哪些线段可能是相等的?有哪些角可能是相等的?底边BC上的高、中线及∠A的平分线有怎样的位置关系?
学生小组讨论并回答猜想结果
发现:
①∠B
=∠C
②∠BAD=∠CAD,AD为顶角的平分线
③∠ADB=∠ADC=90°AD为底边上的高
④BD=CD,AD为底边上的中线
教师利用几何画板演示等腰三角形对折过程,进一步验证学生的
猜想并提出
如何证明发现的命题
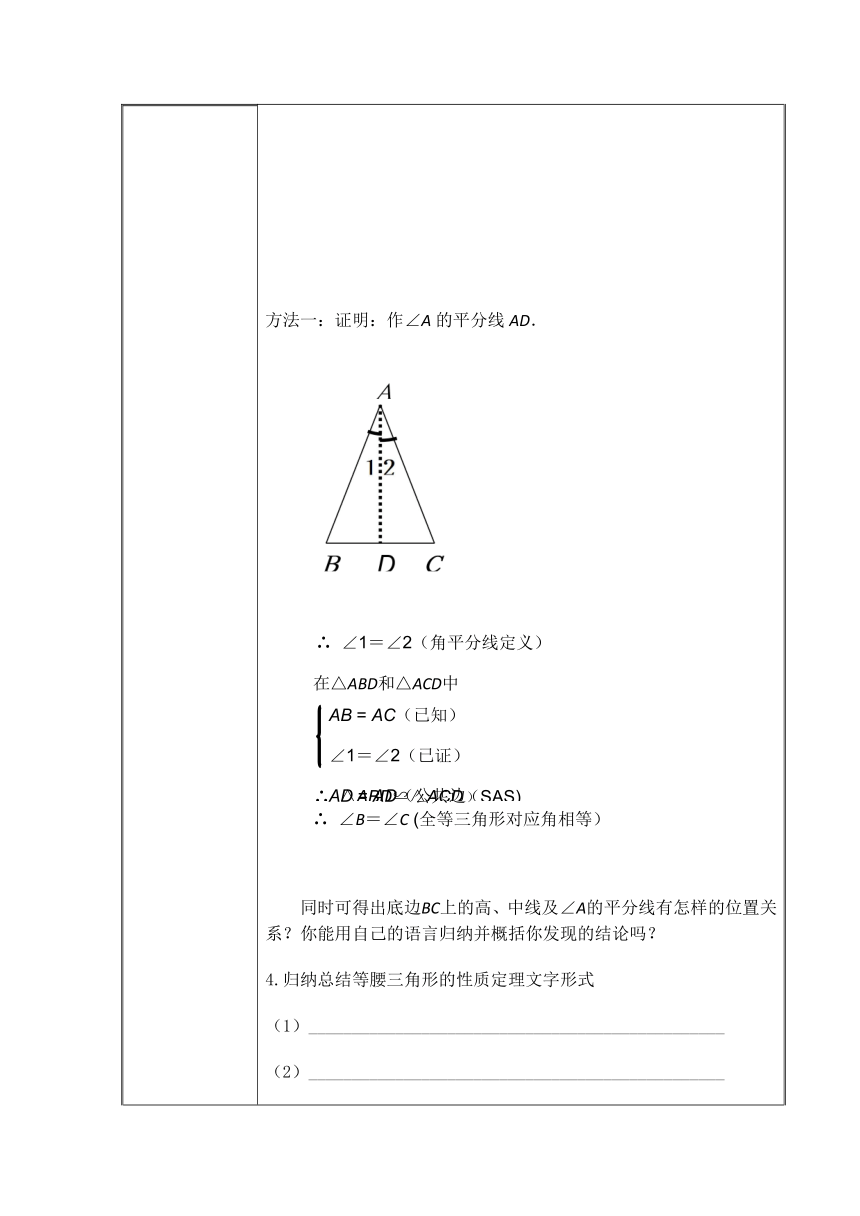
3.推理证明,验证猜想:(注意引导学生做不同的辅助线证明)
已知:如图,⊿ABC中,AB=AC.求证:∠B
=
∠C.
方法一:证明:作∠A的平分线AD.
同时可得出底边BC上的高、中线及∠A的平分线有怎样的位置关系?你能用自己的语言归纳并概括你发现的结论吗?
4.归纳总结等腰三角形的性质定理文字形式
(1)________________________________________________
(2)________________________________________________
(3)________________________________________________
等腰三角形性质定理的应用形式:
根据性质定理,已知:如图,在△ABC中,
⑴∵AB=AC
∴
∠____=∠____
⑵∵AB=AC
,AD⊥BC,∴∠____
=∠
____
,____
=____
⑶∵AB=AC
,BD=CD,∴____
⊥____
,∠____=
∠____
⑷∵AB=AC
,AD是顶角的平分线,∴____
⊥____
,∠____
=∠
____
(三)利用新知,尝试应用
1.快速抢答:
(1)已知:在△ABC中,AB
=
AC,并且其中一个角为80°,那么其他角的度数分别为__________________________.
(2)已知:在△ABC中,AB
=
AC,并且其中一个角为100°,那么其他角的度数分别为________________________.
(3)
如图△ABC是一个屋顶的平面示意图,已知屋椽AB=AC,立柱AD⊥BC,底角∠B=40°,梁长BC=10米,则顶架上∠CAD=_________,BD
=_______米.
2.根据等腰三角形的性质探究等边三角形的性质
三边都相等的三角形叫做等边三角形,等边三角形是等腰三角形的特例,
等边三角形的角又分别有怎样的关系呢?能证明你发现的命题吗?
已知:如图,在△ABC中,AB=BC=AC.
求证:
∠A=
∠B=∠C=60°.
总结归纳等边三角形的性质定理:
________________________________________________
巩固练习,拓展延伸
如图,在△ABC中,
AB=AC,BD,CE
分别为∠ABC,∠ACB
的平分线.
求证:BD=CE.
如图,在△ABC中,
AB=AC,点D在AC上,且BD=BC=AD,指出图中所有的等腰三角形并求∠A
的度数
(五)小结收获,当堂检测
小结:通过本节课的学习,你有什么收获
达标检测
等腰三角形的顶角为80°,则它的底角是____________
一个等腰三角形两边的长分别为4和9,那么这个三角形的周长是____________
如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C=________
4.若等腰三角形中有一个角等于50°,则这个等腰三角形顶角的度数为____________
5.已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形顶角的度数为___________
6.如图,PQ是△ABC的边BC上两点,且BP=PQ=QC=PA=AQ,则∠BAC=________
教学反思
《等腰三角形的性质》这节课重点是让学生通过动手翻折等腰三角形纸片得出“等腰三角形的两底角相等”及“三线合一”的性质。设计理念是让学生通过折纸、猜想、验证等腰三角形的性质,然后运用全等三角形的知识加以论证。使学生思维由形象直观过渡到抽象的逻辑演绎,层层展开,步步深入,从而实现教学目标。我首先用生活中的图片引入等腰三角形的基本图形,联系生活,创设问题情境,把问题作为教学的出发点,激发学生的学习兴趣。引出学生探究心理,迅速集中注意力,使其带着浓厚的兴趣开始积极探索思考。在本节课的问题设置中,由易到难,根据学生的认知特点,易于接受,但是本节课也有很多不足之处,比如课堂气氛不够活跃,后面的巩固练习层次不够全面,由于时间分配不太合理,导致后半部分时间紧张,尤其是当堂检测没来得及细致处理,另外对信息技术软件应用较少,今后要多学习与数学相关的信息技术软件,力求课堂形式多样,内容丰富
教学目标
(一)知识与技能
1.了解等腰三角形和等边三角形相关概念
2.知道等腰三角形是轴对称图形,能利用轴对称图形的性质探索并证明等腰三角形和等边三角形的性质进行
3.能运用等腰三角形的性质进行推理和计算
(二)过程与方法
1.在等腰三角形性质的应用过程中提高学生的合情推理和演绎推理能力,培养学生观察猜想,合作探究的能力
2.体会方程思想在几何计算问题中的渗透与应用
(三)情感态度
通过学生的动手操作,合作探究激发学生解决问题的热情和团结协作的能力
教学重难点
教学重点
用等腰三角形性质定理去解决相关问题
教学难点
在等腰三角形性质的应用过程中提高学生学生的推理能力
学情分析
八年级学生观察操作猜想能力较强,但思维的灵活性不够,自主探究与合作能力也需要在课堂上逐步引导,前面学生已经学习了轴对称的性质,应引导学生用轴对称的性质去猜想等腰三角形的相关性质
教学方法
观察法,发现法,动手操作法,多媒体演示,合作探究法
教学过程
(一)创设情境,引入课题
在学生观察生活中的一些图片时,问:
1.这些图片中抽象出的平面几何图形(如房屋的钢梁架、红领巾、交通标志的外沿形状等),它们有什么共同特点?
2.你能根据这个共同特点给等腰三角形下定义吗?
有两边相等的三角形叫做等腰三角形.
介绍在等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
如图,在△ABC中,AB
=
AC.AB和
AC是腰,BC是底边,∠A是顶角,∠B和∠C是底角,
顶角是直角的等腰三角形叫做等腰直角三角形.
探索新知,渐进升华
1.动手操作,观察猜想
你能利用一张长方形的纸片和工具,借助折纸的方法剪出一个等腰三角形吗?动手做一做(要求学生课前完成)
观察所剪的三角形,思考下面的问题
(1)如图,你认为等腰△ABC是轴对称图形吗?
如果是,对称轴是哪条直线?
根据你的观察,说一说图中有哪些线段可能是相等的?有哪些角可能是相等的?底边BC上的高、中线及∠A的平分线有怎样的位置关系?
学生小组讨论并回答猜想结果
发现:
①∠B
=∠C
②∠BAD=∠CAD,AD为顶角的平分线
③∠ADB=∠ADC=90°AD为底边上的高
④BD=CD,AD为底边上的中线
教师利用几何画板演示等腰三角形对折过程,进一步验证学生的
猜想并提出
如何证明发现的命题
3.推理证明,验证猜想:(注意引导学生做不同的辅助线证明)
已知:如图,⊿ABC中,AB=AC.求证:∠B
=
∠C.
方法一:证明:作∠A的平分线AD.
同时可得出底边BC上的高、中线及∠A的平分线有怎样的位置关系?你能用自己的语言归纳并概括你发现的结论吗?
4.归纳总结等腰三角形的性质定理文字形式
(1)________________________________________________
(2)________________________________________________
(3)________________________________________________
等腰三角形性质定理的应用形式:
根据性质定理,已知:如图,在△ABC中,
⑴∵AB=AC
∴
∠____=∠____
⑵∵AB=AC
,AD⊥BC,∴∠____
=∠
____
,____
=____
⑶∵AB=AC
,BD=CD,∴____
⊥____
,∠____=
∠____
⑷∵AB=AC
,AD是顶角的平分线,∴____
⊥____
,∠____
=∠
____
(三)利用新知,尝试应用
1.快速抢答:
(1)已知:在△ABC中,AB
=
AC,并且其中一个角为80°,那么其他角的度数分别为__________________________.
(2)已知:在△ABC中,AB
=
AC,并且其中一个角为100°,那么其他角的度数分别为________________________.
(3)
如图△ABC是一个屋顶的平面示意图,已知屋椽AB=AC,立柱AD⊥BC,底角∠B=40°,梁长BC=10米,则顶架上∠CAD=_________,BD
=_______米.
2.根据等腰三角形的性质探究等边三角形的性质
三边都相等的三角形叫做等边三角形,等边三角形是等腰三角形的特例,
等边三角形的角又分别有怎样的关系呢?能证明你发现的命题吗?
已知:如图,在△ABC中,AB=BC=AC.
求证:
∠A=
∠B=∠C=60°.
总结归纳等边三角形的性质定理:
________________________________________________
巩固练习,拓展延伸
如图,在△ABC中,
AB=AC,BD,CE
分别为∠ABC,∠ACB
的平分线.
求证:BD=CE.
如图,在△ABC中,
AB=AC,点D在AC上,且BD=BC=AD,指出图中所有的等腰三角形并求∠A
的度数
(五)小结收获,当堂检测
小结:通过本节课的学习,你有什么收获
达标检测
等腰三角形的顶角为80°,则它的底角是____________
一个等腰三角形两边的长分别为4和9,那么这个三角形的周长是____________
如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C=________
4.若等腰三角形中有一个角等于50°,则这个等腰三角形顶角的度数为____________
5.已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形顶角的度数为___________
6.如图,PQ是△ABC的边BC上两点,且BP=PQ=QC=PA=AQ,则∠BAC=________
教学反思
《等腰三角形的性质》这节课重点是让学生通过动手翻折等腰三角形纸片得出“等腰三角形的两底角相等”及“三线合一”的性质。设计理念是让学生通过折纸、猜想、验证等腰三角形的性质,然后运用全等三角形的知识加以论证。使学生思维由形象直观过渡到抽象的逻辑演绎,层层展开,步步深入,从而实现教学目标。我首先用生活中的图片引入等腰三角形的基本图形,联系生活,创设问题情境,把问题作为教学的出发点,激发学生的学习兴趣。引出学生探究心理,迅速集中注意力,使其带着浓厚的兴趣开始积极探索思考。在本节课的问题设置中,由易到难,根据学生的认知特点,易于接受,但是本节课也有很多不足之处,比如课堂气氛不够活跃,后面的巩固练习层次不够全面,由于时间分配不太合理,导致后半部分时间紧张,尤其是当堂检测没来得及细致处理,另外对信息技术软件应用较少,今后要多学习与数学相关的信息技术软件,力求课堂形式多样,内容丰富
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
