冀教版初中数学八年级上册 17.2 含30°角的直角三角形的性质 教案
文档属性
| 名称 | 冀教版初中数学八年级上册 17.2 含30°角的直角三角形的性质 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 113.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 12:10:27 | ||
图片预览


文档简介
含30°角的直角三角形的性质
—30
°角所对的直角边与斜边的关系的教学设计
教学目标
(一)教学知识点
1.探索──发现──猜想──证明直角三角形中有一个角为30°的性质。
2.有一个角为30°的直角三角形的性质的简单应用。
(二)能力训练要求
1.经历“探索──发现──猜想──证明”的过程,引导学生体会合情推理与演绎推理的相互依赖和相互补充的辩证关系。
2.培养学生用规范的数学语言进行表达的习惯和能力。
(三)情感态度与价值观
1.
鼓励学生积极参与数学活动,激发学生的好奇心和求知欲。
2.
体验数学活动中的探索与创新、感受数学的严谨性。
教学重点
含30°角的直角三角形的性质定理的发现与证明。
教学难点
1.含30°角的直角三角形性质定理的探索与证明。
2.引导学生全面、周到地思考问题。
教学方法
探索发现法
教具准备
两个全等的含30°角的三角尺,多媒体
教学过程
一、课前预习
活动(量一量):画出斜边AB=2cm,3cm,4cm,5cm,6cm且∠B=30°的5个直角三角形。分别测量每个直角三角形中斜边AB和AC的长度,发现AC和AB之间的数量关系。
设计意图:通过课前画图测量,学生首先从测量长度感知30°角所对的直角边等于斜边的一半,从而引出本节课探究的标题。
二、探究新知
1、活动一:利用手中的含30°角的直角三角形进行折叠,探索能否得到30°角所对的直角边和斜边的数量关系?
要求:先独立思考动手操作;再小组讨论交流有几种折叠方式,并思考这样做的依据。
设计意图:通过折叠活动,让学生发现结论,为理论证明提供思路。
2、活动二:同桌之间合作用两个全等的含30°角的三角板,能拼出等边三角形吗?并说明理由。
问题:你能借助这个图形,找到含30°角的直角
△ABC
的直角边BC
与斜边AB
之间有什么数量关系吗?
设计意图:让学生经历拼摆三角尺的活动,发现结论,同时引导学生意识到,通过实际操作探索出来的结论,还需要给予证明。
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
3、活动三:教师提出:
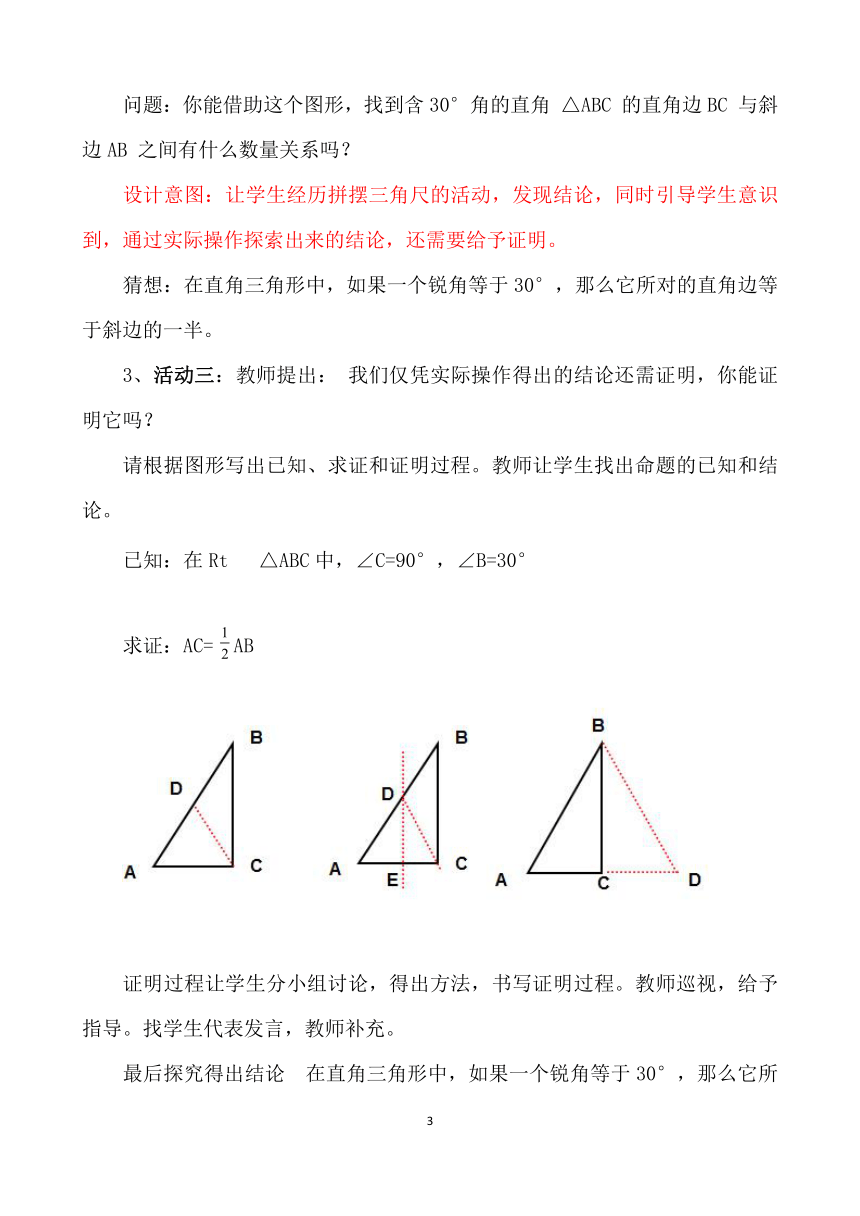
我们仅凭实际操作得出的结论还需证明,你能证明它吗?
请根据图形写出已知、求证和证明过程。教师让学生找出命题的已知和结论。
已知:在Rt△ABC中,∠C=90°,∠B=30°
求证:AC=
AB
证明过程让学生分小组讨论,得出方法,书写证明过程。教师巡视,给予指导。找学生代表发言,教师补充。
最后探究得出结论
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
∵在Rt△ABC中,∠C=90°,∠B=30°
∴AC=
AB
设计意图:引导学生从三角尺的摆拼过程中得到启发,延长AC至D,使CD=AC,连接BD.
让学生发散思维寻找不同的证明方法。
三、课堂练习
1、如图,在△ABC
中,∠C
=90°,∠B
=
30°,AB
=10,则AC
的长为_________
。
2、如图,在△ABC
中,∠C
=90°,
∠A=2∠B
,AC=3cm,则AB=__________。
3、如图,在△ABC
中,∠C
=90°,∠B
=
30°,AB+AC
=12,则AC
的长为_________。
设计意图:学生都能基本答对这三道基础练习题,从而练习本节课的学习知识点。
四、例题讲解
1、在△ABC
中,
∠ACB
=90°,CD是边AB上的高,
∠A
=30°,求证:BD=
AB
设计意图:教师板书证明过程,让学生掌握证明题中如何应用含30度角的直角三角形的性质。
2、在Rt
△ABC
中,已知
∠ACB
=90°,
∠B
=15°,AB边的垂直平分线交AB于点E,交BC与点D,BD=10cm,求AC的长。
先让学生自己书写,教师巡视,最后学生回答,教师总结。
设计意图:让学生自己先书写过程,培养学生的证明能力和学习能力。
五、课堂小结
在直角三角形中,30°所对的直角边等于斜边的一半。
∵
在Rt△ABC中,∠C=90°,∠B=30°
∴
AC=
AB
六、布置作业
1、课本149页A组第三题写到作业本上。
2、若一个等腰三角形的底角是15°,腰长为6cm,求这个等腰三角形腰上的高。
(让学生自己画图,找出含
30°角的直角三角形。)
教学反思
通过本节课的教学,让学生通过自主探索得出本节课的教学重点,学生表现得非常积极。但是在证明含30度角的直角三角形的性质的过程中,有一部分学生的证明思路比较狭窄,需要教师不断引导。另外,本节课时间分配上有些欠妥,在折纸活动中耗费时间比较长,导致学生练习较少,没能发挥练习题的重要性,下次授课应该更合理的安排。
5
—30
°角所对的直角边与斜边的关系的教学设计
教学目标
(一)教学知识点
1.探索──发现──猜想──证明直角三角形中有一个角为30°的性质。
2.有一个角为30°的直角三角形的性质的简单应用。
(二)能力训练要求
1.经历“探索──发现──猜想──证明”的过程,引导学生体会合情推理与演绎推理的相互依赖和相互补充的辩证关系。
2.培养学生用规范的数学语言进行表达的习惯和能力。
(三)情感态度与价值观
1.
鼓励学生积极参与数学活动,激发学生的好奇心和求知欲。
2.
体验数学活动中的探索与创新、感受数学的严谨性。
教学重点
含30°角的直角三角形的性质定理的发现与证明。
教学难点
1.含30°角的直角三角形性质定理的探索与证明。
2.引导学生全面、周到地思考问题。
教学方法
探索发现法
教具准备
两个全等的含30°角的三角尺,多媒体
教学过程
一、课前预习
活动(量一量):画出斜边AB=2cm,3cm,4cm,5cm,6cm且∠B=30°的5个直角三角形。分别测量每个直角三角形中斜边AB和AC的长度,发现AC和AB之间的数量关系。
设计意图:通过课前画图测量,学生首先从测量长度感知30°角所对的直角边等于斜边的一半,从而引出本节课探究的标题。
二、探究新知
1、活动一:利用手中的含30°角的直角三角形进行折叠,探索能否得到30°角所对的直角边和斜边的数量关系?
要求:先独立思考动手操作;再小组讨论交流有几种折叠方式,并思考这样做的依据。
设计意图:通过折叠活动,让学生发现结论,为理论证明提供思路。
2、活动二:同桌之间合作用两个全等的含30°角的三角板,能拼出等边三角形吗?并说明理由。
问题:你能借助这个图形,找到含30°角的直角
△ABC
的直角边BC
与斜边AB
之间有什么数量关系吗?
设计意图:让学生经历拼摆三角尺的活动,发现结论,同时引导学生意识到,通过实际操作探索出来的结论,还需要给予证明。
猜想:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
3、活动三:教师提出:
我们仅凭实际操作得出的结论还需证明,你能证明它吗?
请根据图形写出已知、求证和证明过程。教师让学生找出命题的已知和结论。
已知:在Rt△ABC中,∠C=90°,∠B=30°
求证:AC=
AB
证明过程让学生分小组讨论,得出方法,书写证明过程。教师巡视,给予指导。找学生代表发言,教师补充。
最后探究得出结论
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
∵在Rt△ABC中,∠C=90°,∠B=30°
∴AC=
AB
设计意图:引导学生从三角尺的摆拼过程中得到启发,延长AC至D,使CD=AC,连接BD.
让学生发散思维寻找不同的证明方法。
三、课堂练习
1、如图,在△ABC
中,∠C
=90°,∠B
=
30°,AB
=10,则AC
的长为_________
。
2、如图,在△ABC
中,∠C
=90°,
∠A=2∠B
,AC=3cm,则AB=__________。
3、如图,在△ABC
中,∠C
=90°,∠B
=
30°,AB+AC
=12,则AC
的长为_________。
设计意图:学生都能基本答对这三道基础练习题,从而练习本节课的学习知识点。
四、例题讲解
1、在△ABC
中,
∠ACB
=90°,CD是边AB上的高,
∠A
=30°,求证:BD=
AB
设计意图:教师板书证明过程,让学生掌握证明题中如何应用含30度角的直角三角形的性质。
2、在Rt
△ABC
中,已知
∠ACB
=90°,
∠B
=15°,AB边的垂直平分线交AB于点E,交BC与点D,BD=10cm,求AC的长。
先让学生自己书写,教师巡视,最后学生回答,教师总结。
设计意图:让学生自己先书写过程,培养学生的证明能力和学习能力。
五、课堂小结
在直角三角形中,30°所对的直角边等于斜边的一半。
∵
在Rt△ABC中,∠C=90°,∠B=30°
∴
AC=
AB
六、布置作业
1、课本149页A组第三题写到作业本上。
2、若一个等腰三角形的底角是15°,腰长为6cm,求这个等腰三角形腰上的高。
(让学生自己画图,找出含
30°角的直角三角形。)
教学反思
通过本节课的教学,让学生通过自主探索得出本节课的教学重点,学生表现得非常积极。但是在证明含30度角的直角三角形的性质的过程中,有一部分学生的证明思路比较狭窄,需要教师不断引导。另外,本节课时间分配上有些欠妥,在折纸活动中耗费时间比较长,导致学生练习较少,没能发挥练习题的重要性,下次授课应该更合理的安排。
5
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
