人教版八年级上册数学教案:14.1.4多项式乘多项式
文档属性
| 名称 | 人教版八年级上册数学教案:14.1.4多项式乘多项式 |

|
|
| 格式 | zip | ||
| 文件大小 | 76.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 00:00:00 | ||
图片预览

文档简介
课题
整式的乘法——多项式乘多项式
课型
新授课
总课时
3课时
第三课时
教学目标
1,探索并了解多项式与多项式相乘的法则
2,会运用法则进行计算.
教学过程
先行独立学习
?
预习课本100——101内容,并完成练习
迁移导入
前面我们学习了单项式乘以单项式,单项式乘以多项式,那么怎样进行多项式与多项式的乘法呢?
先学检测或展示
学生提前预习的课堂十分钟(老师先批阅,然后让学生有目标的听课,知道错误的原因)
课堂交互学习
环节一
多项式乘多项式的法则
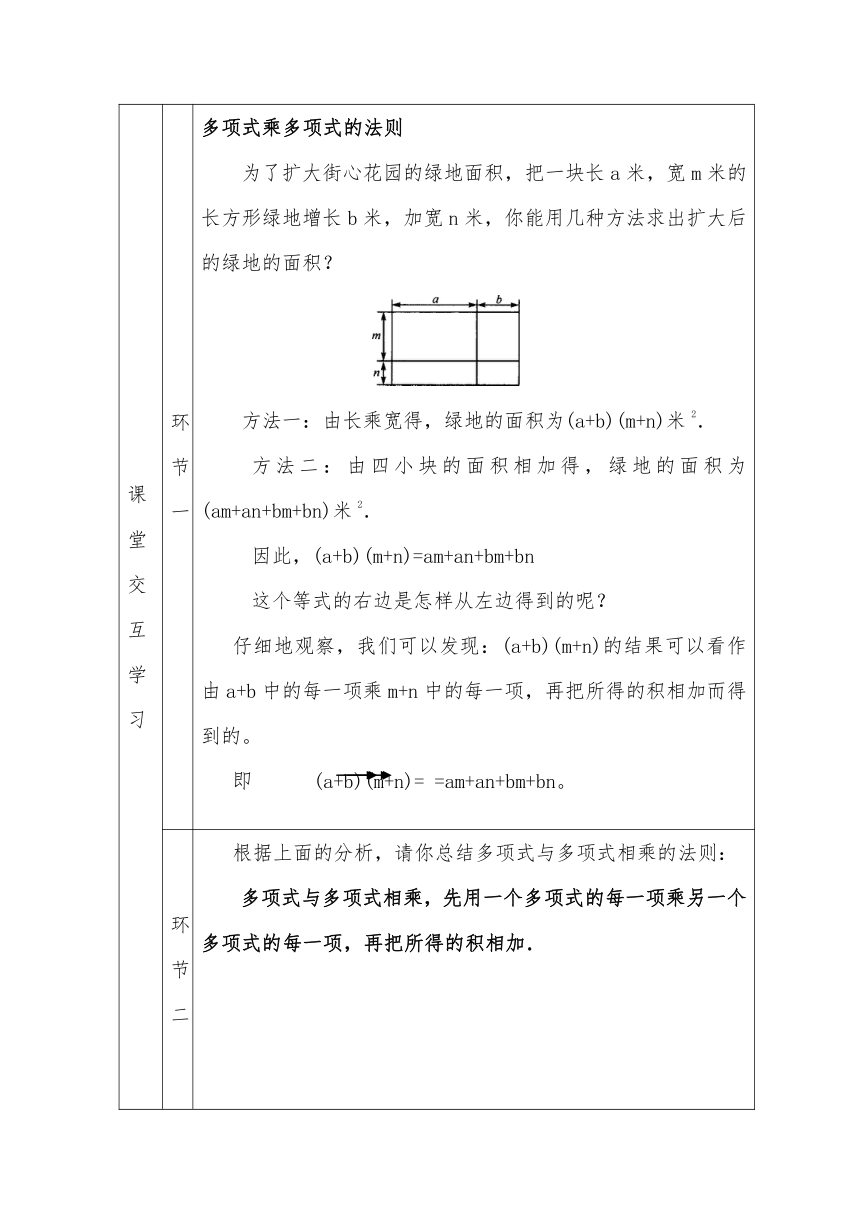
为了扩大街心花园的绿地面积,把一块长a米,宽m米的长方形绿地增长b米,加宽n米,你能用几种方法求出扩大后的绿地的面积?
方法一:由长乘宽得,绿地的面积为(a+b)(m+n)米2.
方法二:由四小块的面积相加得,绿地的面积为(am+an+bm+bn)米2.
因此,(a+b)(m+n)=am+an+bm+bn
这个等式的右边是怎样从左边得到的呢?
仔细地观察,我们可以发现:(a+b)(m+n)的结果可以看作由a+b中的每一项乘m+n中的每一项,再把所得的积相加而得到的。
即
(a+b)(m+n)=
=am+an+bm+bn。
环节二
根据上面的分析,请你总结多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
环节三
例1计算:(1)(3x+1)(x+2);
(2)(x-8)(x-y);
(3)(x+y)(x2-xy+y2)。
分析:这是什么运算?怎样进行这样的运算?
解:(1)(3x+1)(x+2)=3x·x+3x·2+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2
(2)(x-8)(x-y)=x·x-xy-8xy+8y2
=x2-9xy+8y2。
(3)(x+y)(x2-xy+y2)=x3-x2y+xy2+x2y-
xy2
+y3
=x3
+y3。
注意:去括号时要注意符号的变化。
整体达标检测
拓展巩固练习
1,观察上面四题的计算结果:二次项系数,一次项系数,常数项有什么关系让学生讨论。
(x+p)(x+q)=(
)x
+(
)x+(
)
2,已知(3x-2x+1)(x+b)中不含x2项,求b
的值。
教学反思
整式的乘法——多项式乘多项式
课型
新授课
总课时
3课时
第三课时
教学目标
1,探索并了解多项式与多项式相乘的法则
2,会运用法则进行计算.
教学过程
先行独立学习
?
预习课本100——101内容,并完成练习
迁移导入
前面我们学习了单项式乘以单项式,单项式乘以多项式,那么怎样进行多项式与多项式的乘法呢?
先学检测或展示
学生提前预习的课堂十分钟(老师先批阅,然后让学生有目标的听课,知道错误的原因)
课堂交互学习
环节一
多项式乘多项式的法则
为了扩大街心花园的绿地面积,把一块长a米,宽m米的长方形绿地增长b米,加宽n米,你能用几种方法求出扩大后的绿地的面积?
方法一:由长乘宽得,绿地的面积为(a+b)(m+n)米2.
方法二:由四小块的面积相加得,绿地的面积为(am+an+bm+bn)米2.
因此,(a+b)(m+n)=am+an+bm+bn
这个等式的右边是怎样从左边得到的呢?
仔细地观察,我们可以发现:(a+b)(m+n)的结果可以看作由a+b中的每一项乘m+n中的每一项,再把所得的积相加而得到的。
即
(a+b)(m+n)=
=am+an+bm+bn。
环节二
根据上面的分析,请你总结多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
环节三
例1计算:(1)(3x+1)(x+2);
(2)(x-8)(x-y);
(3)(x+y)(x2-xy+y2)。
分析:这是什么运算?怎样进行这样的运算?
解:(1)(3x+1)(x+2)=3x·x+3x·2+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2
(2)(x-8)(x-y)=x·x-xy-8xy+8y2
=x2-9xy+8y2。
(3)(x+y)(x2-xy+y2)=x3-x2y+xy2+x2y-
xy2
+y3
=x3
+y3。
注意:去括号时要注意符号的变化。
整体达标检测
拓展巩固练习
1,观察上面四题的计算结果:二次项系数,一次项系数,常数项有什么关系让学生讨论。
(x+p)(x+q)=(
)x
+(
)x+(
)
2,已知(3x-2x+1)(x+b)中不含x2项,求b
的值。
教学反思
