苏科版八年级上册第六章一次函数教案(拓展提高)
文档属性
| 名称 | 苏科版八年级上册第六章一次函数教案(拓展提高) |  | |
| 格式 | zip | ||
| 文件大小 | 95.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 13:01:24 | ||
图片预览




文档简介
教学内容
一次函数
教学目标
强化分类讨论思想,掌握常考题型
重点
分类讨论
难点
理解概念,并灵活运用
教学过程
一次函数:
函数是研究现实世界变化规律的一个重要模型,它是变量数学的标志。“函数”是从量的侧面去描述客观世界的运动变化、相互关系。
函数叫做一次函数,它的图像是一条直线,与一次函数相关的知识有:
画直线时,一般选点(0,b)和点();
函数中的系数k,b的正负性,决定图像的大致位置以及y随x的变化情况,|k|表示直线的倾斜程度,|k|越大,直线越陡,反之越平缓。
平移、旋转、翻折是直线在坐标系中运动的基本形式
设直线,直线
若∥,则且
若,则
例题精讲:
例1:如图1,在平面直角坐标系中,M是直线上的动点,过点M做MN⊥x轴,交直线于点N,当时,设点M的横坐标为m,则m的取值范围为
变式:有一种动画程序,屏幕上正方形区域ABCD表示黑色物体甲,如图2,其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线发射信号,当信号遇到甲区域时,甲由黑变白,则b的取值范围为
时,甲能由黑变白
图1
图2
例2:已知函数的图像如图3所示,则的图像可能是(
)
A.
B.
C.
D.
图3
变式:如图,平面直角坐标系中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时点Q从点A出发向点B运动,当点Q到达点B时,点P,Q同时停止运动,若点P和点Q的速度之比为1∶2,则下列说法正确的是(
)
A.
线段PQ始终经过点(2,3)
B.
线段PQ始终经过点(3,2)
C.
线段PQ始终经过点(2,2)
D.
线段PQ不可能始终经过某一点
例3:1号探测气球从海拔5m处出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处以0.5m/min匀速上升,两个气球都上升了50min,设气球上升时间为xmin(0≤x≤50)
根据题意填写下表:
上升时间/min1030……x1号探测气球所在位置的海拔/m15……2号探测气球所在位置的海拔/m30……
在某个时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由
当30≤x≤50时,两个气球所在位置的海拔最多差多少米?
例4:如图,在平面直角坐标系中,已知正比例函数与一次函数的图像交于点A
求点A的坐标
设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图像于点B,C,连接OC,若BC=OA,求△OBC的面积
例5:对于平面直角坐标系中任意两点,,我们把叫做,两点间的直角距离,记做
已知O为坐标原点,动点P(x,y)满足,请写出x与y之间满足关系式,并在直角坐标系中画出所有符合条件的点P所组成的图形
设是一定点,Q(x,y)是直线上的动点,我们把的最小值叫做到直线的直角距离,试求点M(2,1)到直线的直角距离
例6:如图,在平面直角坐标系中,直线分别交x轴、y轴于点A,B,将△AOB绕点O顺时针旋转90°后得到△A’OB’
求直线A’B’的解析式
若直线A’B’与直线相交于点C,求△A’OB的面积
综合练习
练习1:已知直线与x轴的交点在A(2,0),B(3,0)之间(包括A、B两点),则a的取值范围是
;在平面直角坐标系中,已知点A(2,3),B(4,7),直线与线段AB有交点,则k的取值范围为
练习2:无论a取什么实数,点P(a-1,2a-3)都在直线上,Q(m,n)是直线上的点,则
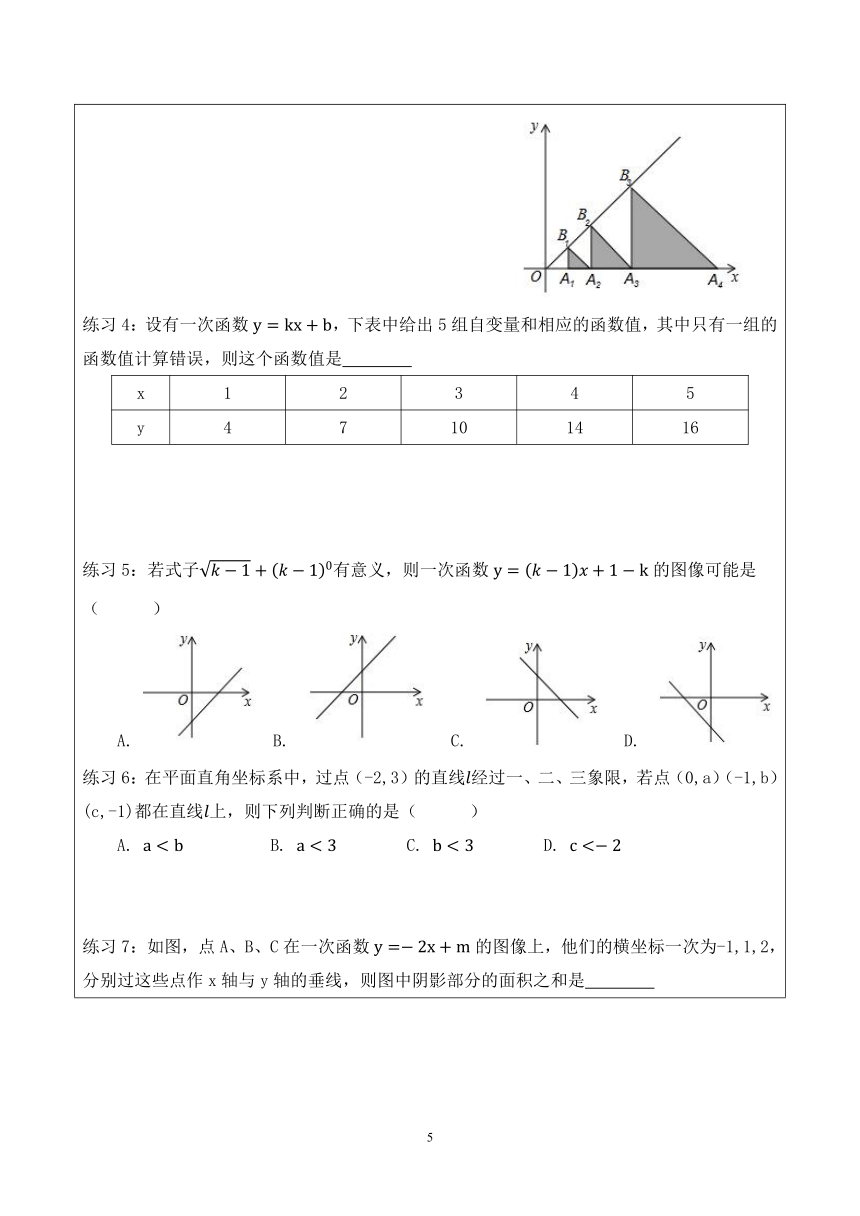
练习3:如图,△,△,△,……,△是等腰直角三角形,其中、、…,,在x轴上,点、、…,,在上,已知,则的长为
练习4:设有一次函数,下表中给出5组自变量和相应的函数值,其中只有一组的函数值计算错误,则这个函数值是
x12345y47101416
练习5:若式子有意义,则一次函数的图像可能是(
)
B.
C.
D.
练习6:在平面直角坐标系中,过点(-2,3)的直线经过一、二、三象限,若点(0,a)(-1,b)(c,-1)都在直线上,则下列判断正确的是(
)
A.
B.
C.
D.
练习7:如图,点A、B、C在一次函数的图像上,他们的横坐标一次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是
练习8:若,直线不经过第四象限,则直线图像一定不经过第
象限
练习9:如图,直线经过点A(-1,0)与点B(2,3),另一条直线经过点B,且与x轴相交与点P(m,0)
求直线的解析式
若△APB的面积为3,求m的值
练习10:如图,在平面直角坐标系中,直线过点A(5,m),且与y轴交于点B,把点A向左平移2个单位长度,再向上平移4个单位长度,得到点C,过点C且与直线平行的直线交y轴于点D
求直线CD的解析式
直线AB与CD交于点E,将直线CD沿EB方向平移至经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围
拓展练习:
练习1:设直线(n为自然数)与坐标轴围成的三角形面积为,则
练习2:一本书的出版成本包括固定成本和变动成本两部分,“稿费+排版费”是固定成本,而“印刷费+纸张费”与印刷的书的数量成正比
现有一种图书,每本定价8元,假定以定价卖出,当印2000册并全部卖出时,出版社不赚不赔;当印3000册全部卖出时,可得利润5000元,则此书的固定成本是
元,如果印4000本全部卖完,出版社可得利润
元
练习3:设一次函数的图像经过点P(1,2),它与x轴、y轴的正半轴分别交于A、B两点,坐标原点为O,若OA+OB=6,则此函数的解析式是
练习4:已知一次函数,当时,对应的y值为,则kb=
;
练习5:一次函数和的图像分别与y轴交于点P和点Q,这两点关于x轴对称,则m的取值是
练习6:在直角坐标系中,直线与两个坐标轴的正半轴行程的三角形的面积等于72,则不在直线上的点的坐标是(
)
A.
(3,12)
B.
(1,20)
C.
(-0,5,26)
D.
(-2.5.32)
练习7:在平面直角坐标系中,点P的坐标为(m+1,m-1)
试判断点P是否在一次函数的图像上,并说明理由
如图,一次函数的图像与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围
练习8:已知四条线,,和所围成的四边形面积是12,求m的值
练习9:某商业集团新进了40台空调机、60台电冰箱,计划调配给下属的甲乙两个连锁销售,其中70台给甲连锁店,30台给乙连锁店,两个连锁店销售这两种电器每台的利润(元)如下表:
空调机电冰箱甲连锁店200170乙连锁店160150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元)
求y关于x的函数关系式,并求出x的取值范围
为了促销,集团决定仅对甲连锁店的空调每台让利a元销售,其他的销售利润不变,并且让利后每条空调机的利润仍高于甲连锁店销售的每台电冰箱的利润,问:该集团应如何设计调配方案,使总利润达到最大?
练习10:平面直角坐标系中,正方形ABCD四个顶点的坐标分别为(-1,-1)(1,-1)(1,1)(-1,1)。设正方形ABCD在的图像以上部分的面积为S,试求S关于a的函数关系式,并写出S的最大值
一次函数
教学目标
强化分类讨论思想,掌握常考题型
重点
分类讨论
难点
理解概念,并灵活运用
教学过程
一次函数:
函数是研究现实世界变化规律的一个重要模型,它是变量数学的标志。“函数”是从量的侧面去描述客观世界的运动变化、相互关系。
函数叫做一次函数,它的图像是一条直线,与一次函数相关的知识有:
画直线时,一般选点(0,b)和点();
函数中的系数k,b的正负性,决定图像的大致位置以及y随x的变化情况,|k|表示直线的倾斜程度,|k|越大,直线越陡,反之越平缓。
平移、旋转、翻折是直线在坐标系中运动的基本形式
设直线,直线
若∥,则且
若,则
例题精讲:
例1:如图1,在平面直角坐标系中,M是直线上的动点,过点M做MN⊥x轴,交直线于点N,当时,设点M的横坐标为m,则m的取值范围为
变式:有一种动画程序,屏幕上正方形区域ABCD表示黑色物体甲,如图2,其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线发射信号,当信号遇到甲区域时,甲由黑变白,则b的取值范围为
时,甲能由黑变白
图1
图2
例2:已知函数的图像如图3所示,则的图像可能是(
)
A.
B.
C.
D.
图3
变式:如图,平面直角坐标系中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时点Q从点A出发向点B运动,当点Q到达点B时,点P,Q同时停止运动,若点P和点Q的速度之比为1∶2,则下列说法正确的是(
)
A.
线段PQ始终经过点(2,3)
B.
线段PQ始终经过点(3,2)
C.
线段PQ始终经过点(2,2)
D.
线段PQ不可能始终经过某一点
例3:1号探测气球从海拔5m处出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处以0.5m/min匀速上升,两个气球都上升了50min,设气球上升时间为xmin(0≤x≤50)
根据题意填写下表:
上升时间/min1030……x1号探测气球所在位置的海拔/m15……2号探测气球所在位置的海拔/m30……
在某个时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由
当30≤x≤50时,两个气球所在位置的海拔最多差多少米?
例4:如图,在平面直角坐标系中,已知正比例函数与一次函数的图像交于点A
求点A的坐标
设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图像于点B,C,连接OC,若BC=OA,求△OBC的面积
例5:对于平面直角坐标系中任意两点,,我们把叫做,两点间的直角距离,记做
已知O为坐标原点,动点P(x,y)满足,请写出x与y之间满足关系式,并在直角坐标系中画出所有符合条件的点P所组成的图形
设是一定点,Q(x,y)是直线上的动点,我们把的最小值叫做到直线的直角距离,试求点M(2,1)到直线的直角距离
例6:如图,在平面直角坐标系中,直线分别交x轴、y轴于点A,B,将△AOB绕点O顺时针旋转90°后得到△A’OB’
求直线A’B’的解析式
若直线A’B’与直线相交于点C,求△A’OB的面积
综合练习
练习1:已知直线与x轴的交点在A(2,0),B(3,0)之间(包括A、B两点),则a的取值范围是
;在平面直角坐标系中,已知点A(2,3),B(4,7),直线与线段AB有交点,则k的取值范围为
练习2:无论a取什么实数,点P(a-1,2a-3)都在直线上,Q(m,n)是直线上的点,则
练习3:如图,△,△,△,……,△是等腰直角三角形,其中、、…,,在x轴上,点、、…,,在上,已知,则的长为
练习4:设有一次函数,下表中给出5组自变量和相应的函数值,其中只有一组的函数值计算错误,则这个函数值是
x12345y47101416
练习5:若式子有意义,则一次函数的图像可能是(
)
B.
C.
D.
练习6:在平面直角坐标系中,过点(-2,3)的直线经过一、二、三象限,若点(0,a)(-1,b)(c,-1)都在直线上,则下列判断正确的是(
)
A.
B.
C.
D.
练习7:如图,点A、B、C在一次函数的图像上,他们的横坐标一次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是
练习8:若,直线不经过第四象限,则直线图像一定不经过第
象限
练习9:如图,直线经过点A(-1,0)与点B(2,3),另一条直线经过点B,且与x轴相交与点P(m,0)
求直线的解析式
若△APB的面积为3,求m的值
练习10:如图,在平面直角坐标系中,直线过点A(5,m),且与y轴交于点B,把点A向左平移2个单位长度,再向上平移4个单位长度,得到点C,过点C且与直线平行的直线交y轴于点D
求直线CD的解析式
直线AB与CD交于点E,将直线CD沿EB方向平移至经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围
拓展练习:
练习1:设直线(n为自然数)与坐标轴围成的三角形面积为,则
练习2:一本书的出版成本包括固定成本和变动成本两部分,“稿费+排版费”是固定成本,而“印刷费+纸张费”与印刷的书的数量成正比
现有一种图书,每本定价8元,假定以定价卖出,当印2000册并全部卖出时,出版社不赚不赔;当印3000册全部卖出时,可得利润5000元,则此书的固定成本是
元,如果印4000本全部卖完,出版社可得利润
元
练习3:设一次函数的图像经过点P(1,2),它与x轴、y轴的正半轴分别交于A、B两点,坐标原点为O,若OA+OB=6,则此函数的解析式是
练习4:已知一次函数,当时,对应的y值为,则kb=
;
练习5:一次函数和的图像分别与y轴交于点P和点Q,这两点关于x轴对称,则m的取值是
练习6:在直角坐标系中,直线与两个坐标轴的正半轴行程的三角形的面积等于72,则不在直线上的点的坐标是(
)
A.
(3,12)
B.
(1,20)
C.
(-0,5,26)
D.
(-2.5.32)
练习7:在平面直角坐标系中,点P的坐标为(m+1,m-1)
试判断点P是否在一次函数的图像上,并说明理由
如图,一次函数的图像与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围
练习8:已知四条线,,和所围成的四边形面积是12,求m的值
练习9:某商业集团新进了40台空调机、60台电冰箱,计划调配给下属的甲乙两个连锁销售,其中70台给甲连锁店,30台给乙连锁店,两个连锁店销售这两种电器每台的利润(元)如下表:
空调机电冰箱甲连锁店200170乙连锁店160150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元)
求y关于x的函数关系式,并求出x的取值范围
为了促销,集团决定仅对甲连锁店的空调每台让利a元销售,其他的销售利润不变,并且让利后每条空调机的利润仍高于甲连锁店销售的每台电冰箱的利润,问:该集团应如何设计调配方案,使总利润达到最大?
练习10:平面直角坐标系中,正方形ABCD四个顶点的坐标分别为(-1,-1)(1,-1)(1,1)(-1,1)。设正方形ABCD在的图像以上部分的面积为S,试求S关于a的函数关系式,并写出S的最大值
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
