第七章 锐角三角函数复习

第11课时 单元复习课
知识梳理
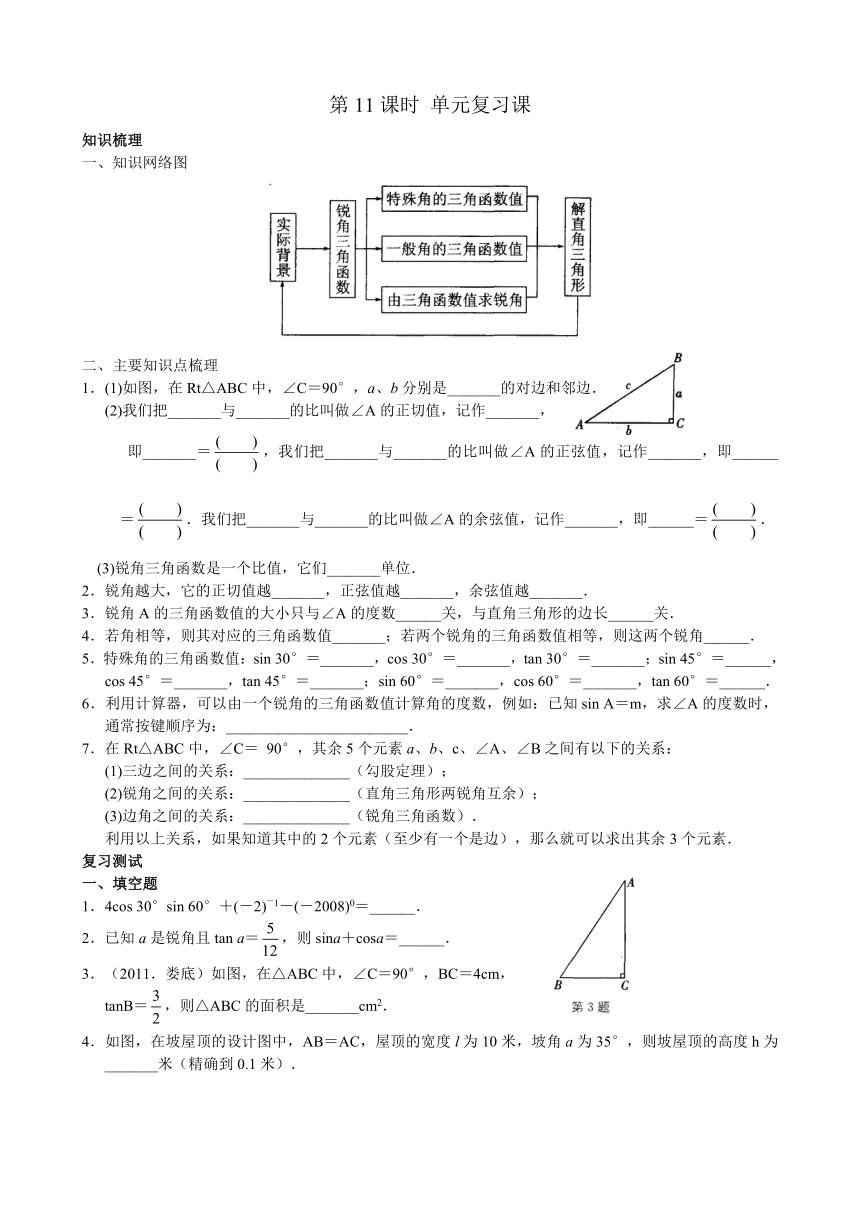
一、知识网络图
二、主要知识点梳理
1．(1)如图，在Rt△ABC中，∠C＝90°，a、b分别是_______的对边和邻边．
(2)我们把_______与_______的比叫做∠A的正切值，记作_______，
即_______＝，我们把_______与_______的比叫做∠A的正弦值，记作_______，即______＝．我们把_______与_______的比叫做∠A的余弦值，记作_______，即______＝．
(3)锐角三角函数是一个比值，它们_______单位．
2．锐角越大，它的正切值越_______，正弦值越_______，余弦值越_______．
3．锐角A的三角函数值的大小只与∠A的度数______关，与直角三角形的边长______关．
4．若角相等，则其对应的三角函数值_______；若两个锐角的三角函数值相等，则这两个锐角______．
5．特殊角的三角函数值：sin 30°＝_______，cos 30°＝_______，tan 30°＝_______；sin 45°＝______，cos 45°＝_______，tan 45°＝_______；sin 60°＝_______，cos 60°＝_______，tan 60°＝______．
6．利用计算器，可以由一个锐角的三角函数值计算角的度数，例如：已知sin A＝m，求∠A的度数时，通常按键顺序为：________________________．
7．在Rt△ABC中，∠C＝ 90°，其余5个元素a、b、c、∠A、∠B之间有以下的关系：
(1)三边之间的关系：______________（勾股定理）；
(2)锐角之间的关系：______________（直角三角形两锐角互余）；
(3)边角之间的关系：______________（锐角三角函数）．
利用以上关系，如果知道其中的2个元素（至少有一个是边），那么就可以求出其余3个元素．
复习测试
一、填空题
1．4cos 30°sin 60°＋(－2)－1－(－2008)0＝______．
2．已知a是锐角且tan a＝，则sina＋cosa＝______．
3．（2011．娄底）如图，在△ABC中，∠C＝90°，BC＝4cm，
tanB＝，则△ABC的面积是_______cm2．
4．如图，在坡屋顶的设计图中，AB＝AC，屋顶的宽度l为10米，坡角a为35°，则坡屋顶的高度h为_______米（精确到0.1米）．
5．(2010．宿迁)如图，在Rt△ABC中，∠C＝90°，AM是BC边上的中线，sin∠CAM＝，则tan B的值为______．
6．(2011．哈尔滨)已知正方形ABCD的边长为2，P是直线CD上一点，若DP＝1，则tan∠BPC的值是______．
二、选择题
7．(2011．荆州)在△ABC中，∠A＝120°，AB＝4，AC＝2，则sinB的值是 ( )
A． B． C． D．
8．（2010．山西）在Rt△ABC中，∠C＝90°，若将各边的长度都扩大为原来的2倍，则∠A的正弦值 ( )
A．扩大2倍 B．缩小为原来的 C．扩大4倍 D．不变
9．在Rt△ABC中，∠C＝90°，tanA＝，则sin B的值为 ( )
A． B． C． D．
10．已知圆锥的底面半径为5 cm，侧面积为65π cm2，设圆锥的母线与高的夹角为θ（如图所示），则sinθ的值为 ( )
A． B． C． D．
11．（2011．镇江）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D．若AC＝，BC＝2，则sin∠ACD的值为 ( )
A． B． C． D．
三、解答题
12．根据下面的条件，求出Rt△ABC(∠C＝90°)中未知的边和角．
(1) BC＝8，∠B＝60°； 　　 (2) AC＝，AB＝2．
13．如图，在Rt△ABC中，∠C＝90°，∠A＝15°．
(1)作AB边的垂直平分线DE，分别交AC、AB于点D、E，连接BD(不写作法，保留作图痕迹)．
(2)在(1)的基础上，求tanA的值．
14．2011年6月份，某地遭暴雨袭击，水位猛涨．某市抗洪抢险救援队伍在B处接到报告：有受灾群众被困于一座遭水淹的楼顶A处，情况危急！救援队伍在B处测得A在B北偏东60°的方向上（如图所示），队伍决定分成两组：第一组马上下水游向A处救人，同时第二组从陆地往正东方向奔跑120米到达C处，再从C处下水游向A处救人．已知A在C北偏东30°的方向上，救援人员在水中行进的速度均为1米／秒，在陆地上奔跑的速度为4米／秒，试问哪组救援队伍先到达A处？请说明理由（≈1.732）．
15．（2011．南京）如图，某数学课外活动小组测量电视塔AB的高度，他们借助一个高度为30 m的建筑物CD进行测量，在点C处测得塔顶B的仰角为45°，在点E处测得B的仰角为37°(B、D、E三点在一条直线上)．求电视塔的高度h(sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)．
16．（2011．黄冈）如图，防洪大堤的横断面是梯形，背水坡AB的坡度i＝1：，且AB＝20 m．身高为1.7 m(即AM≈1.7 m)的小明站在大堤A点，测得高压电线杆端点D的仰角为30°．已知地面CB宽30 m，求高压电线杆CD的高度（结果保留三个有效数字，≈1.732）．
17．如图，河边有一条笔直的公路l，公路的两侧是平坦的草地．在数学活动课上，老师让同学们测量河对岸B点到公路l之间的距离．请你设计一个测量方案，要求：
(1)列出你测量时所使用的测量工具．
(2)画出测量的示意图，写出测量的步骤．
(3)用字母表示测得的数据，求出点B到公路l之间的距离．
18．如图，一辆汽车在一个十字路口遇到红灯刹车停下，汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA＝30°和∠DCB＝60°．如果斑马线的宽度AB是3米，驾驶员与车头的距离是0.8米，那么这时汽车车头与斑马线的距离x是多少米？
19．如图，电工李师傅借助梯子安装天花板上距地面2.90 m的顶灯．已知梯子由两个相同的矩形面组成，每个矩形面的长都被六条踏板七等分，使用时梯脚的固定跨度为1 m．矩形面与地面所成的角a为78°．李师傅的身高为1.78 m，当他攀升到头顶距天花板0.05～0.20 m时，安装起来比较方便，他现在竖直站立在梯子的第三级踏板上，请你通过计算判断他安装起来是否比较方便(sin 78°≈0.98，cos 78°≈0.21，tan 78°≈4.70)．
参考答案
1． 2． 3．12 4．3.5 5． 6．2或
7．D 8．D 9．D 10．B 11．A
12．(1)∠A＝30°，AB＝16，AC＝8 (2)∠A＝∠B＝45°，BC＝
13．(1)略 (2) 2－
14．第二组
15．电视塔的高度约为120 m
16．≈39.0 (m)
17．(1)测角器、卷尺 (2)测量示意图如图所示 测量步骤略 (3)设点B到CD的距离为x米，
18．x＝0.7
19．他安装起来比较方便