人教版八年级下册数学 17.1勾股定理 同步测试(Word版 含解析)
文档属性
| 名称 | 人教版八年级下册数学 17.1勾股定理 同步测试(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 08:50:44 | ||
图片预览



文档简介
17.1勾股定理 同步测试
一.选择题
1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为25 B.三角形的周长为25
C.三角形的面积为12 D.斜边长为5
2.已知直角三角形的三边长为三个连续整数,那么,这个三角形的面积是( )
A.6 B.8 C.10 D.12
3.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
4.如图,在4×4的方格纸中,有一个格点三角形ABC,关于它的描述正确的是( )
A.三边长都是有理数 B.是等腰三角形
C.是直角三角形 D.有一条边长为5
5.在Rt△ABC中,∠C=90°,已知a:b=3:4,c=10,其中a,b,c分别为∠A,∠B,∠C的对边,则a的长为( )
A.3 B.6 C.8 D.12
6.在Rt△ABC中,∠C=90°,已知c2=2b2,则该三角形中两直角边的关系是( )
A.a>b
B.a<b
C.a=b
D.以上都有可能,不能确定
7.以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则S1,S2,S3之间的关系是( )
A.S1+S2>S3 B.S1+S2<S3
C.S1+S2=S3 D.S12+S22=S32
8.如图,在边长为1的正方形网格中,从点A出发,连接AB,AC,AD,AE,AF,其中B,C,D,E,F都是网格上的点,在以上五条线段中,长度是无理数的线段有( )
A.5条 B.4条 C.3条 D.2条
9.如图是一株美丽的勾股树,其中所有四边形都是正方形,所有的三角形都是直角三角形若正方形A、B、C、D的面积分别为3、5、2、3,则最大正方形E的面积是( )
A.47 B.13 C.11 D.8
10.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD=AC,点D在AB上,AF⊥CD交于点E,交CB于点F,则CF的长是( )
A.2.5 B.2 C.1.8 D.1.5
二.填空题
11.如图,在△ABC中,已知AB=2,AC=4,BC=6.则△ABC的面积为 .
12.如图,在△ABC中,点D边BC上一点,∠DAC=∠B=45°,AB=6,BC=,则△ABD的面积是 .
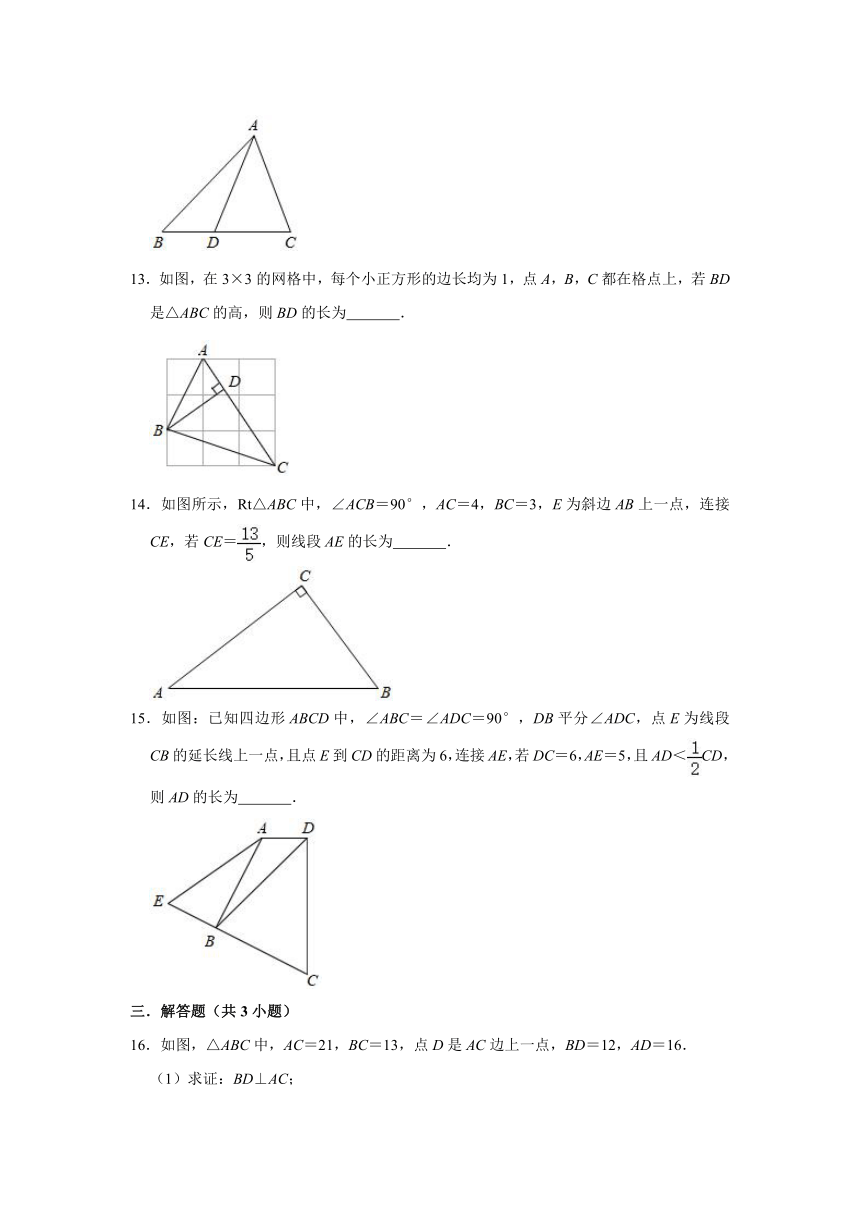
13.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为 .
14.如图所示,Rt△ABC中,∠ACB=90°,AC=4,BC=3,E为斜边AB上一点,连接CE,若CE=,则线段AE的长为 .
15.如图:已知四边形ABCD中,∠ABC=∠ADC=90°,DB平分∠ADC,点E为线段CB的延长线上一点,且点E到CD的距离为6,连接AE,若DC=6,AE=5,且AD<CD,则AD的长为 .
三.解答题(共3小题)
16.如图,△ABC中,AC=21,BC=13,点D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若点E是AB边上的动点,连接DE,求线段DE的最小值.
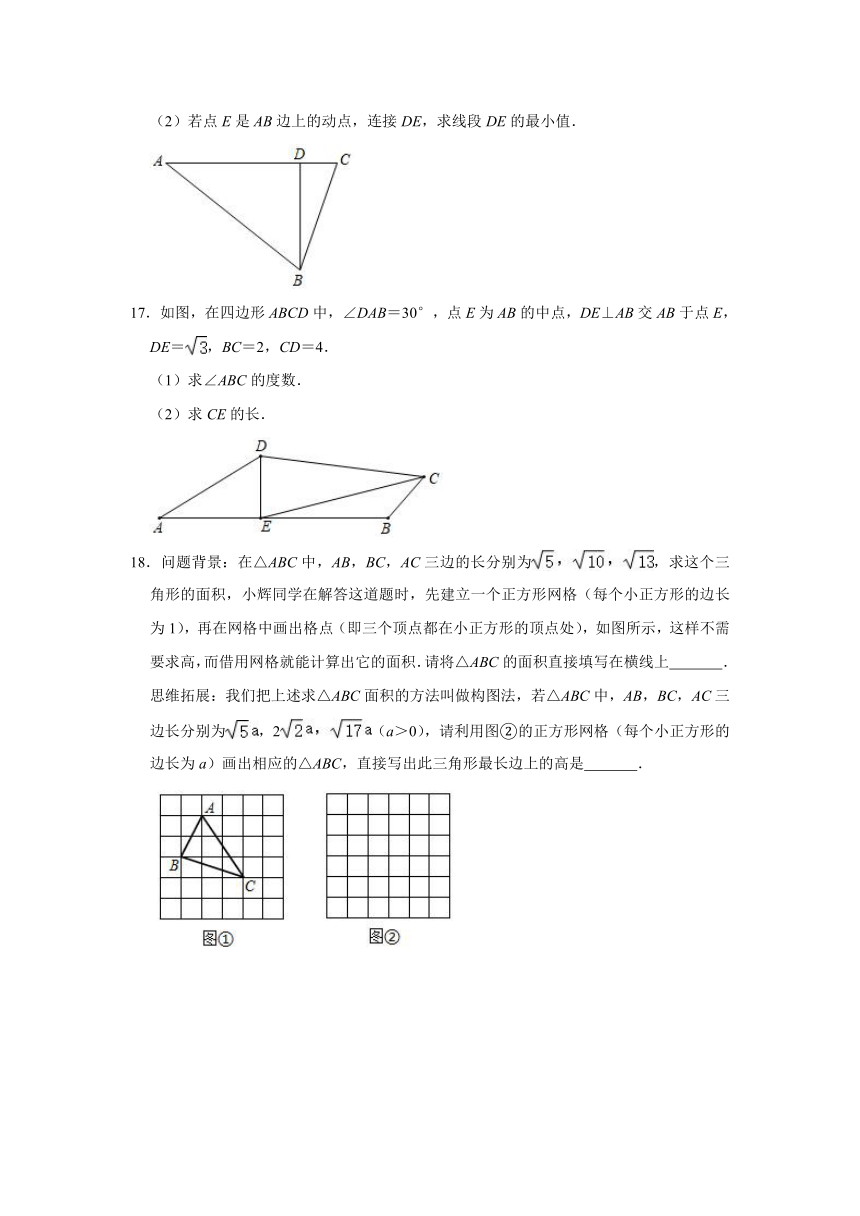
17.如图,在四边形ABCD中,∠DAB=30°,点E为AB的中点,DE⊥AB交AB于点E,DE=,BC=2,CD=4.
(1)求∠ABC的度数.
(2)求CE的长.
18.问题背景:在△ABC中,AB,BC,AC三边的长分别为,求这个三角形的面积,小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图所示,这样不需要求高,而借用网格就能计算出它的面积.请将△ABC的面积直接填写在横线上 .
思维拓展:我们把上述求△ABC面积的方法叫做构图法,若△ABC中,AB,BC,AC三边长分别为,2(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,直接写出此三角形最长边上的高是 .
参考答案
一.选择题
1.解:根据勾股定理可知,直角三角形两直角边长分别为3和4,
则它的斜边长是=5,
周长是3+4+5=12,
三角形的面积=×3×4=6,
故说法正确的是D选项.
故选:D.
2.解:设这三边长分别为x,x+1,x+2,
根据勾股定理得:(x+2)2=(x+1)2+x2
解得:x=﹣1(不合题意舍去),或x=3,
∴x+1=4,x+2=5,
则三边长是3,4,5,
∴三角形的面积=××4=6;
故选:A.
3.解:如图所示,
∵∠A=90°,
∴b2+c2=a2.
故选:B.
4.解:由勾股定理得:AC==5,AB==,BC==,
结合问题的选项可知答案D是正确的,
故选:D.
5.解:由a:b=3:4,设a=3k,b=4k,
在Rt△ABC中,a=3k,b=4k,c=10,
根据勾股定理得:a2+b2=c2,即9k2+16k2=100,
解得:k=2或k=﹣2(舍去),
则a=3k=6.
故选:B.
6.解:根据勾股定理得:c2=a2+b2,∵c2=2b2,∴a2=b2,
∵线段都是正数,∴a=b.
故选:C.
7.解:设直角三角形三边分别为a,b,c,则a2+b2=c2
以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则分别是,,,
∴它们之间的关系为S1+S2=S3
故选:C.
8.解:根据勾股定理计算得:
在直角△ABM中,AB===,
同理可得:AC=;AD=;AE=;AF=
所以长度是无理数的线段有AB,AC,AD,AE,AF,故选A.
9.解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:
x2=3+5=8;
y2=2+3=5;
z2=x2+y2=13.
故最大正方形E的面积是z2=13.
故选:B.
10.解:连接DF,如图所示:
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵AD=AC=3,AF⊥CD,
∴CE=DE,BD=AB﹣AD=2,
∴CF=DF,
在△ADF和△ACF中,,
∴△ADF≌△ACF(SSS),
∴∠ADF=∠ACF=90°,
∴∠BDF=90°,
设CF=DF=x,则BF=4﹣x,
在Rt△BDF中,由勾股定理得:DF2+BD2=BF2,
即x2+22=(4﹣x)2,
解得:x=1.5;
∴CF=1.5;
故选:D.
二.填空题
11.解:如图,过A作AD⊥BC于D,
设BD=x,则CD=6﹣x,
依题意有(2)2﹣x2=(4)2﹣(6﹣x)2,
解得x=2,
在Rt△ADB中,AD===4,
则△ABC的面积为×6×4=12.
故答案为:12.
12.解:如图,过点A作EA⊥AB交BC的延长线于E,过点C作CF⊥AE于点F,过点A作AG⊥BC于G,
∵∠B=45°,
∴∠E=90°﹣45°=45°,
∴AE=AB=6,
由勾股定理得BE==6,
∴AG=3,CE=BE﹣BC=2,
∵EF⊥AE,∠E=45°,
∴△CFE为等腰直角三角形,
∴CF=FE=CE=2,
∴AF=AE﹣EF=4,
在Rt△ACF中,
AC==2,
∵∠DAC=∠B=45°,∠ACB=∠ACB,
∴△ACB∽△DCA,
∴=,
∴=,
∴DC=,
∴BD=BC﹣DC=,
∴△ABD的面积=×BD×AG=××3=.
故答案为:.
13.解:由勾股定理得:AC=,
∵S△ABC=3×3﹣,
∴,
∴,
∴BD=,
故答案为:.
14.解:∵∠ACB=90°,AC=4,BC=3,
∴AB==5,
过C作CD⊥AB于D,
∴∠CDA=∠CDB=90°,CD===,
∴AD==,
∵CE=,
∴DE==1,
∴AE=AD﹣DE=或AE=AD+DE=,
故答案为:或.
15.解:如图,连接AC,过点E作EH⊥CD于H,作ET⊥DA,交DA的延长线于T,过点C作CR⊥TE,交TE的延长线于R,
∵∠DTE=∠EHD=∠HDT=90°,
∴四边形EHDT是矩形,
∴EH=DT=6,
∵CD=6,
∴DT=CD,
∵∠R=∠T=∠CDT=90°,
∴四边形CDTR是矩形,
∵DC=DT,
∴四边形CDTR是正方形,
延长TD到K,使得DK=RE,连接CK.
∵RC=DC,RE=DK,∠ERC=∠CDK=90°,
∴△CRE≌△CDK(SAS),
∴CE=CK,∠ECR=∠DCK,
∴∠RCD=∠ECK=90°,
∵BD平分∠ADC,
∴∠BDA=∠BDC=45°,
∵∠ABC=∠ADC=90°,
∴∠ABC+∠ADC=180°,
∴A,B,C,D四点共圆,
∴∠ACB=∠ADB=45°,
∴∠ACE=∠ACK=45°,
∵CA=CA,
∴△CAE≌△CAK(SAS),
∴AE=AK=AD+DK=AD+ER=5
设AD=x,则ER=5﹣x,ET=6﹣(5﹣x)=1+x,AT=6﹣x,
在Rt△AET中,则有52=(6﹣x)2+(1+x)2,
解得x=2或3(舍弃),
∴AD=2.
故答案为2.
三.解答题(共3小题)
16.解:(1)∵AC=21,AD=16,
∴CD=AC﹣AD=5,
∵BD2+CD2=122+52=169=BC2,
∴∠BDC=90°,
∴BD⊥AC.
(2)当DE⊥AB时,DE最短,
∵AB==20,
∵?AD?DB=?AB?DE,
∴DE==9.6,
∴线段DE使得最小值为9.6.
17.解:(1)连接BD,作CF⊥AB于F,如图所示:
则∠BFC=90°,
∵点E为AB的中点,DE⊥AB,
∴BD=AD,AE=BE,
∵∠DAB=30°,
∴∠DBE=∠DAB=30°,BD=AD=2DE=2,AE=BE=DE=3,
∵BC2+BD2=22+(2)2=16=CD2,
∴△BCD是直角三角形,∠CBD=90°,
∴∠ABC=∠ABD+∠CBD=30°+90°=120°;
(2)由(1)可得:∠CBF=180°﹣30°﹣90°=60°,
∴∠BCF=30°,∠BFC=90°,
∴∠BCF=30°,
∴BF=BC=1,CF=BF=,
∴EF=BE+BF=4,
在Rt△CEF中,由勾股定理得:CE==.
18.解:问题背景:S△ABC=3×3﹣×1×2﹣×1×3﹣×2×3=.
思维拓展:如图作BH⊥AC于H.
∵S△ABC=?AC?BH=2a×4a﹣×2a×2a﹣×a×2a﹣×a×4a=3a2,
∴×a×BH=3a2,
∴BH=a.
一.选择题
1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为25 B.三角形的周长为25
C.三角形的面积为12 D.斜边长为5
2.已知直角三角形的三边长为三个连续整数,那么,这个三角形的面积是( )
A.6 B.8 C.10 D.12
3.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
4.如图,在4×4的方格纸中,有一个格点三角形ABC,关于它的描述正确的是( )
A.三边长都是有理数 B.是等腰三角形
C.是直角三角形 D.有一条边长为5
5.在Rt△ABC中,∠C=90°,已知a:b=3:4,c=10,其中a,b,c分别为∠A,∠B,∠C的对边,则a的长为( )
A.3 B.6 C.8 D.12
6.在Rt△ABC中,∠C=90°,已知c2=2b2,则该三角形中两直角边的关系是( )
A.a>b
B.a<b
C.a=b
D.以上都有可能,不能确定
7.以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则S1,S2,S3之间的关系是( )
A.S1+S2>S3 B.S1+S2<S3
C.S1+S2=S3 D.S12+S22=S32
8.如图,在边长为1的正方形网格中,从点A出发,连接AB,AC,AD,AE,AF,其中B,C,D,E,F都是网格上的点,在以上五条线段中,长度是无理数的线段有( )
A.5条 B.4条 C.3条 D.2条
9.如图是一株美丽的勾股树,其中所有四边形都是正方形,所有的三角形都是直角三角形若正方形A、B、C、D的面积分别为3、5、2、3,则最大正方形E的面积是( )
A.47 B.13 C.11 D.8
10.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD=AC,点D在AB上,AF⊥CD交于点E,交CB于点F,则CF的长是( )
A.2.5 B.2 C.1.8 D.1.5
二.填空题
11.如图,在△ABC中,已知AB=2,AC=4,BC=6.则△ABC的面积为 .
12.如图,在△ABC中,点D边BC上一点,∠DAC=∠B=45°,AB=6,BC=,则△ABD的面积是 .
13.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为 .
14.如图所示,Rt△ABC中,∠ACB=90°,AC=4,BC=3,E为斜边AB上一点,连接CE,若CE=,则线段AE的长为 .
15.如图:已知四边形ABCD中,∠ABC=∠ADC=90°,DB平分∠ADC,点E为线段CB的延长线上一点,且点E到CD的距离为6,连接AE,若DC=6,AE=5,且AD<CD,则AD的长为 .
三.解答题(共3小题)
16.如图,△ABC中,AC=21,BC=13,点D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若点E是AB边上的动点,连接DE,求线段DE的最小值.
17.如图,在四边形ABCD中,∠DAB=30°,点E为AB的中点,DE⊥AB交AB于点E,DE=,BC=2,CD=4.
(1)求∠ABC的度数.
(2)求CE的长.
18.问题背景:在△ABC中,AB,BC,AC三边的长分别为,求这个三角形的面积,小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图所示,这样不需要求高,而借用网格就能计算出它的面积.请将△ABC的面积直接填写在横线上 .
思维拓展:我们把上述求△ABC面积的方法叫做构图法,若△ABC中,AB,BC,AC三边长分别为,2(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,直接写出此三角形最长边上的高是 .
参考答案
一.选择题
1.解:根据勾股定理可知,直角三角形两直角边长分别为3和4,
则它的斜边长是=5,
周长是3+4+5=12,
三角形的面积=×3×4=6,
故说法正确的是D选项.
故选:D.
2.解:设这三边长分别为x,x+1,x+2,
根据勾股定理得:(x+2)2=(x+1)2+x2
解得:x=﹣1(不合题意舍去),或x=3,
∴x+1=4,x+2=5,
则三边长是3,4,5,
∴三角形的面积=××4=6;
故选:A.
3.解:如图所示,
∵∠A=90°,
∴b2+c2=a2.
故选:B.
4.解:由勾股定理得:AC==5,AB==,BC==,
结合问题的选项可知答案D是正确的,
故选:D.
5.解:由a:b=3:4,设a=3k,b=4k,
在Rt△ABC中,a=3k,b=4k,c=10,
根据勾股定理得:a2+b2=c2,即9k2+16k2=100,
解得:k=2或k=﹣2(舍去),
则a=3k=6.
故选:B.
6.解:根据勾股定理得:c2=a2+b2,∵c2=2b2,∴a2=b2,
∵线段都是正数,∴a=b.
故选:C.
7.解:设直角三角形三边分别为a,b,c,则a2+b2=c2
以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则分别是,,,
∴它们之间的关系为S1+S2=S3
故选:C.
8.解:根据勾股定理计算得:
在直角△ABM中,AB===,
同理可得:AC=;AD=;AE=;AF=
所以长度是无理数的线段有AB,AC,AD,AE,AF,故选A.
9.解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:
x2=3+5=8;
y2=2+3=5;
z2=x2+y2=13.
故最大正方形E的面积是z2=13.
故选:B.
10.解:连接DF,如图所示:
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵AD=AC=3,AF⊥CD,
∴CE=DE,BD=AB﹣AD=2,
∴CF=DF,
在△ADF和△ACF中,,
∴△ADF≌△ACF(SSS),
∴∠ADF=∠ACF=90°,
∴∠BDF=90°,
设CF=DF=x,则BF=4﹣x,
在Rt△BDF中,由勾股定理得:DF2+BD2=BF2,
即x2+22=(4﹣x)2,
解得:x=1.5;
∴CF=1.5;
故选:D.
二.填空题
11.解:如图,过A作AD⊥BC于D,
设BD=x,则CD=6﹣x,
依题意有(2)2﹣x2=(4)2﹣(6﹣x)2,
解得x=2,
在Rt△ADB中,AD===4,
则△ABC的面积为×6×4=12.
故答案为:12.
12.解:如图,过点A作EA⊥AB交BC的延长线于E,过点C作CF⊥AE于点F,过点A作AG⊥BC于G,
∵∠B=45°,
∴∠E=90°﹣45°=45°,
∴AE=AB=6,
由勾股定理得BE==6,
∴AG=3,CE=BE﹣BC=2,
∵EF⊥AE,∠E=45°,
∴△CFE为等腰直角三角形,
∴CF=FE=CE=2,
∴AF=AE﹣EF=4,
在Rt△ACF中,
AC==2,
∵∠DAC=∠B=45°,∠ACB=∠ACB,
∴△ACB∽△DCA,
∴=,
∴=,
∴DC=,
∴BD=BC﹣DC=,
∴△ABD的面积=×BD×AG=××3=.
故答案为:.
13.解:由勾股定理得:AC=,
∵S△ABC=3×3﹣,
∴,
∴,
∴BD=,
故答案为:.
14.解:∵∠ACB=90°,AC=4,BC=3,
∴AB==5,
过C作CD⊥AB于D,
∴∠CDA=∠CDB=90°,CD===,
∴AD==,
∵CE=,
∴DE==1,
∴AE=AD﹣DE=或AE=AD+DE=,
故答案为:或.
15.解:如图,连接AC,过点E作EH⊥CD于H,作ET⊥DA,交DA的延长线于T,过点C作CR⊥TE,交TE的延长线于R,
∵∠DTE=∠EHD=∠HDT=90°,
∴四边形EHDT是矩形,
∴EH=DT=6,
∵CD=6,
∴DT=CD,
∵∠R=∠T=∠CDT=90°,
∴四边形CDTR是矩形,
∵DC=DT,
∴四边形CDTR是正方形,
延长TD到K,使得DK=RE,连接CK.
∵RC=DC,RE=DK,∠ERC=∠CDK=90°,
∴△CRE≌△CDK(SAS),
∴CE=CK,∠ECR=∠DCK,
∴∠RCD=∠ECK=90°,
∵BD平分∠ADC,
∴∠BDA=∠BDC=45°,
∵∠ABC=∠ADC=90°,
∴∠ABC+∠ADC=180°,
∴A,B,C,D四点共圆,
∴∠ACB=∠ADB=45°,
∴∠ACE=∠ACK=45°,
∵CA=CA,
∴△CAE≌△CAK(SAS),
∴AE=AK=AD+DK=AD+ER=5
设AD=x,则ER=5﹣x,ET=6﹣(5﹣x)=1+x,AT=6﹣x,
在Rt△AET中,则有52=(6﹣x)2+(1+x)2,
解得x=2或3(舍弃),
∴AD=2.
故答案为2.
三.解答题(共3小题)
16.解:(1)∵AC=21,AD=16,
∴CD=AC﹣AD=5,
∵BD2+CD2=122+52=169=BC2,
∴∠BDC=90°,
∴BD⊥AC.
(2)当DE⊥AB时,DE最短,
∵AB==20,
∵?AD?DB=?AB?DE,
∴DE==9.6,
∴线段DE使得最小值为9.6.
17.解:(1)连接BD,作CF⊥AB于F,如图所示:
则∠BFC=90°,
∵点E为AB的中点,DE⊥AB,
∴BD=AD,AE=BE,
∵∠DAB=30°,
∴∠DBE=∠DAB=30°,BD=AD=2DE=2,AE=BE=DE=3,
∵BC2+BD2=22+(2)2=16=CD2,
∴△BCD是直角三角形,∠CBD=90°,
∴∠ABC=∠ABD+∠CBD=30°+90°=120°;
(2)由(1)可得:∠CBF=180°﹣30°﹣90°=60°,
∴∠BCF=30°,∠BFC=90°,
∴∠BCF=30°,
∴BF=BC=1,CF=BF=,
∴EF=BE+BF=4,
在Rt△CEF中,由勾股定理得:CE==.
18.解:问题背景:S△ABC=3×3﹣×1×2﹣×1×3﹣×2×3=.
思维拓展:如图作BH⊥AC于H.
∵S△ABC=?AC?BH=2a×4a﹣×2a×2a﹣×a×2a﹣×a×4a=3a2,
∴×a×BH=3a2,
∴BH=a.
