11第二十二章 一元二次方程
文档属性
| 名称 | 11第二十二章 一元二次方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 449.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 一元二次方程
一、新课导入
-3
8
-1
二、典型问题
三、归纳小结
四、阶梯训练
D
B
-3
23
1
五、考题链接
(一)学习目标
1.会根据具体问题列出一元二次方程,体会方程
的模型思想
2.理解一元二次方程的概念和一元二次方程根
的意义,会把
元二次方程化为一般形式,能判
断一元二次方程的二次项系数、次项系数和常数项
(二)课前预习
【检测1】一个数x比另一个数大3,且这两个数
之积为88,求这个数x,列方程为
检测2】方程(2x-1)-3x(x-2)=0整理为一
般形式
,二次项系数是
一次项系数是
常数项是
★一元二次方程的辨别
例1判断下列方程哪些是一元二次方程
(1)42=81;(2)2(x2-1)=3y2;
(3)5x2-1=4x;(4)
0:
N+
x
(5)3x(x-1)=5(x+2)
(6)关于x的方程mx2-3x+2=0
分析:利用一元二次方程的定义:①方程两边都
是整式;②只含有一个未知数(元);③未知数的最膏
次数是2进行判断
变式
1)x2-1=3m2是关于x的元二次方程吗
(2)3x(5x-1)=5x(3x+2)是一元二次方程吗
为什么
(3)当k满足什么条件时,关于x的方程(k-2)2+
x-3=0是元二次方程
变式1(1)是;
(2)不是,因为化简后不含二次项;
(3)k≠2时,是元二次方程
★一元二次方程的一般形式
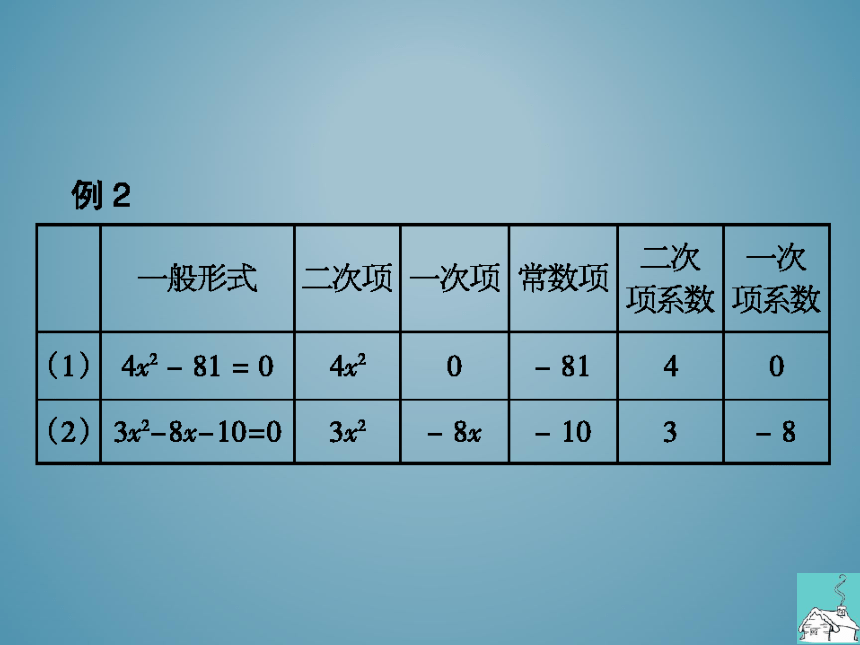
例2将下列元二次方程化为一般形式,并分
别指出它们的一次项、次项和常数项及它们的系数
(1)4x2=81;(2)3x(x-1)=5(x+2)
分析:经过整理,将方程化为一般形式ax2+bx+
c=0(a≠0)后再对应确定即可,注意系数的符号
例2
一般形式一次项一次项常数项
二次一次
项系数项系数
(1)42-81=0420
814
0
(2)3x2-8x-10=03
&x
将方程3x(x-m)=5(x+m)整理成关于x的
元二次方程的般形式,并分别指出它们的二次项、
次项和常数项及它们的系数
变式2一般形式为3x2-(3m+5)x-5m=0,二次
项是3x2,次项是-(3m+5)x,常数项是-5m,二次项
系数为3,一次项系数为-3m-5
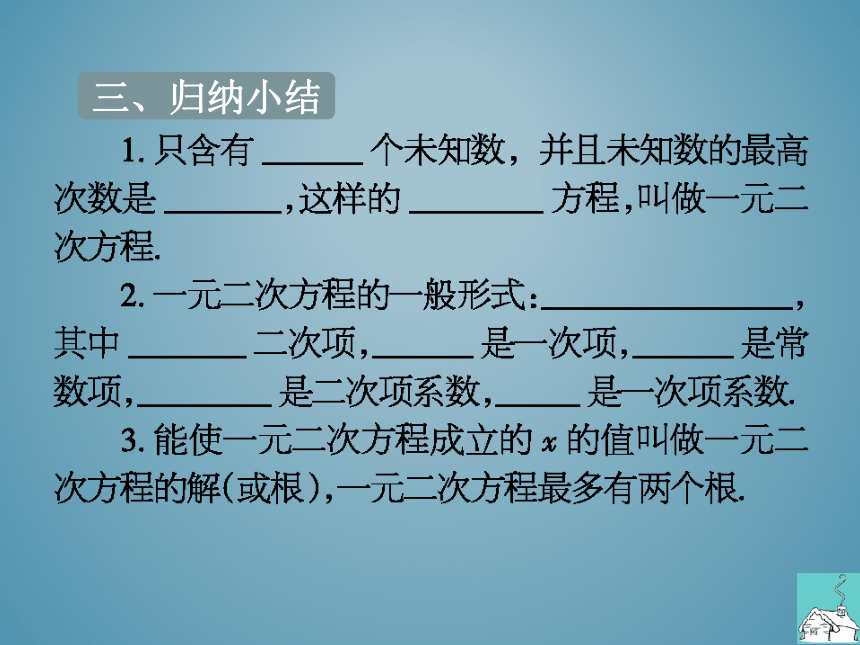
1.只含有
个未知数,并且未知数的最高
次数是
这样的
方程,叫做一元二
次方程
2.一元二次方程的般形式:
其中
二次项
是一次项
是常
数项,
是二次项系数,是次项系数
3.能使一元二次方程成立的x的值叫做一元二
次方程的解(或根),一元二次方程最多有两个根.
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 一元二次方程
一、新课导入
-3
8
-1
二、典型问题
三、归纳小结
四、阶梯训练
D
B
-3
23
1
五、考题链接
(一)学习目标
1.会根据具体问题列出一元二次方程,体会方程
的模型思想
2.理解一元二次方程的概念和一元二次方程根
的意义,会把
元二次方程化为一般形式,能判
断一元二次方程的二次项系数、次项系数和常数项
(二)课前预习
【检测1】一个数x比另一个数大3,且这两个数
之积为88,求这个数x,列方程为
检测2】方程(2x-1)-3x(x-2)=0整理为一
般形式
,二次项系数是
一次项系数是
常数项是
★一元二次方程的辨别
例1判断下列方程哪些是一元二次方程
(1)42=81;(2)2(x2-1)=3y2;
(3)5x2-1=4x;(4)
0:
N+
x
(5)3x(x-1)=5(x+2)
(6)关于x的方程mx2-3x+2=0
分析:利用一元二次方程的定义:①方程两边都
是整式;②只含有一个未知数(元);③未知数的最膏
次数是2进行判断
变式
1)x2-1=3m2是关于x的元二次方程吗
(2)3x(5x-1)=5x(3x+2)是一元二次方程吗
为什么
(3)当k满足什么条件时,关于x的方程(k-2)2+
x-3=0是元二次方程
变式1(1)是;
(2)不是,因为化简后不含二次项;
(3)k≠2时,是元二次方程
★一元二次方程的一般形式
例2将下列元二次方程化为一般形式,并分
别指出它们的一次项、次项和常数项及它们的系数
(1)4x2=81;(2)3x(x-1)=5(x+2)
分析:经过整理,将方程化为一般形式ax2+bx+
c=0(a≠0)后再对应确定即可,注意系数的符号
例2
一般形式一次项一次项常数项
二次一次
项系数项系数
(1)42-81=0420
814
0
(2)3x2-8x-10=03
&x
将方程3x(x-m)=5(x+m)整理成关于x的
元二次方程的般形式,并分别指出它们的二次项、
次项和常数项及它们的系数
变式2一般形式为3x2-(3m+5)x-5m=0,二次
项是3x2,次项是-(3m+5)x,常数项是-5m,二次项
系数为3,一次项系数为-3m-5
1.只含有
个未知数,并且未知数的最高
次数是
这样的
方程,叫做一元二
次方程
2.一元二次方程的般形式:
其中
二次项
是一次项
是常
数项,
是二次项系数,是次项系数
3.能使一元二次方程成立的x的值叫做一元二
次方程的解(或根),一元二次方程最多有两个根.
同课章节目录
