12第二十二章 配方法
图片预览




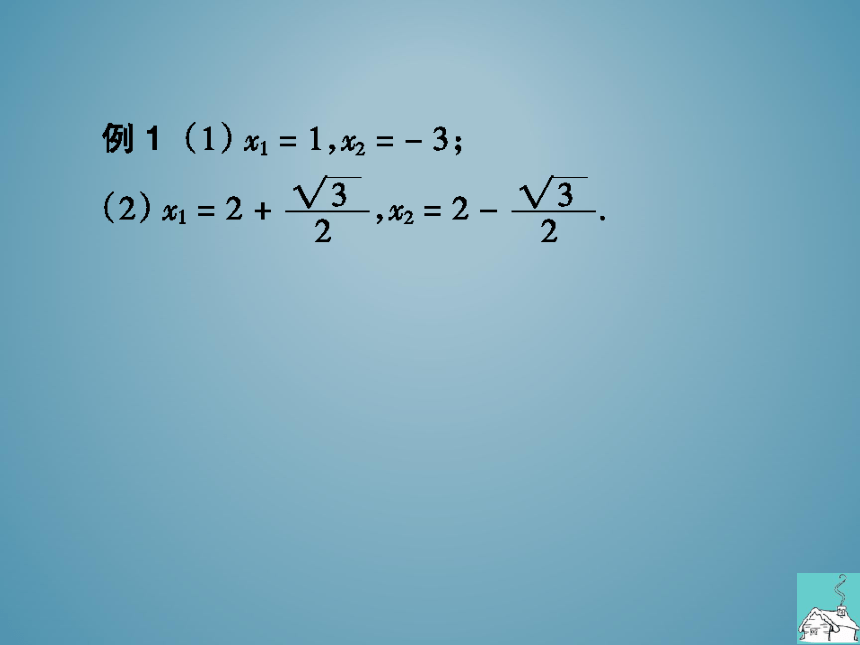


文档简介
(共17张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 配方法
一、新课导入
A
16
4
49
7
二、典型问题
三、归纳小结
四、阶梯训练
B
C
9
3
16
4
D
五、考题链接
(一)学习目标
1.会解形如x2=p(p≥0)或(mx+n)2=p(p≥0)
形式的方程
2.掌握用配方法解一元二次方程的一般步骤,会
用配方法解一元二次方程.
3.初步理解根据具体问题中的数量关系列出
元二次方程并求解,能依据实际情境检验结果的合
理性
(二)课前预习
检测1】一元二次方程x2-4=0的解是()
A.x1=2,x2=-2
B.x=-2
【检测2】把下列各多项式配方:
(1)x2+8x+=(x+_)2;
(2)x2-14x+
)2.
★用直接开平方法解方程
例1解下列方程:
(1)(x+1)2-4=0;(2)12(2-x)2-9=0
分析:两个方程都先转化为(mx+n)2=p(p≥0
的形式,再直接开平方解方程
变式1
解方程:x2+6x+9
16
★用配方法解方程
例2解下列方程:
(1)x2-2x-2=0;(2)2x2+1=3x
分析:(1)二次项系数是1,方程两边加上一次项
系数一半的平方后进行配方;(2)二次项系数不等于1,
方程两边同除以二次项系数,将其化为1,然后再配方
例2(1)x1=1+√3,x2=1-V3;
(2)x1=1,=2
藏变式2
当x取何值时,代数式x(x-8)的值与4-2x+2x2
的值相等
变式2当x=-3+V5或x=-3-V5时,代数
式x(x-8)与4-2x+2x2的值相等
1.通过配成完全平方形式来解一元二次方程的
方法,叫做
,其关键是方程两边同时加上
2.配方法是解一元二次方程的重要方法,它隐含
着创造条件实现化归的思想,是中学数学中一个重要
的解题方法
A组:基础练习
1.用配方法解方程x2-2x-5=0时,原方程应
变形为
A.(x+1)2=6
B.(x-1)2=6
C.(x+2)2=9
D.(x-2)2=9
2.解方程(x+1)2=9的解为
().
A.x=2
B.x=-4
C
D
2
3.填空
x+6x+
x
(2)x2-8x+(
x+x十
()=(x+_)2
4解下列方程:
1)x2+8x-2=0
(2)x2-5x-6=0
(3)2x2-x=6
4.(1)x1=3V2-4,x=-3V2-4;
(2)x1=-1,x=6;(3)x
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 配方法
一、新课导入
A
16
4
49
7
二、典型问题
三、归纳小结
四、阶梯训练
B
C
9
3
16
4
D
五、考题链接
(一)学习目标
1.会解形如x2=p(p≥0)或(mx+n)2=p(p≥0)
形式的方程
2.掌握用配方法解一元二次方程的一般步骤,会
用配方法解一元二次方程.
3.初步理解根据具体问题中的数量关系列出
元二次方程并求解,能依据实际情境检验结果的合
理性
(二)课前预习
检测1】一元二次方程x2-4=0的解是()
A.x1=2,x2=-2
B.x=-2
【检测2】把下列各多项式配方:
(1)x2+8x+=(x+_)2;
(2)x2-14x+
)2.
★用直接开平方法解方程
例1解下列方程:
(1)(x+1)2-4=0;(2)12(2-x)2-9=0
分析:两个方程都先转化为(mx+n)2=p(p≥0
的形式,再直接开平方解方程
变式1
解方程:x2+6x+9
16
★用配方法解方程
例2解下列方程:
(1)x2-2x-2=0;(2)2x2+1=3x
分析:(1)二次项系数是1,方程两边加上一次项
系数一半的平方后进行配方;(2)二次项系数不等于1,
方程两边同除以二次项系数,将其化为1,然后再配方
例2(1)x1=1+√3,x2=1-V3;
(2)x1=1,=2
藏变式2
当x取何值时,代数式x(x-8)的值与4-2x+2x2
的值相等
变式2当x=-3+V5或x=-3-V5时,代数
式x(x-8)与4-2x+2x2的值相等
1.通过配成完全平方形式来解一元二次方程的
方法,叫做
,其关键是方程两边同时加上
2.配方法是解一元二次方程的重要方法,它隐含
着创造条件实现化归的思想,是中学数学中一个重要
的解题方法
A组:基础练习
1.用配方法解方程x2-2x-5=0时,原方程应
变形为
A.(x+1)2=6
B.(x-1)2=6
C.(x+2)2=9
D.(x-2)2=9
2.解方程(x+1)2=9的解为
().
A.x=2
B.x=-4
C
D
2
3.填空
x+6x+
x
(2)x2-8x+(
x+x十
()=(x+_)2
4解下列方程:
1)x2+8x-2=0
(2)x2-5x-6=0
(3)2x2-x=6
4.(1)x1=3V2-4,x=-3V2-4;
(2)x1=-1,x=6;(3)x
同课章节目录
