14第二十二章 因式分解法
文档属性
| 名称 | 14第二十二章 因式分解法 |  | |
| 格式 | zip | ||
| 文件大小 | 354.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:46:07 | ||
图片预览





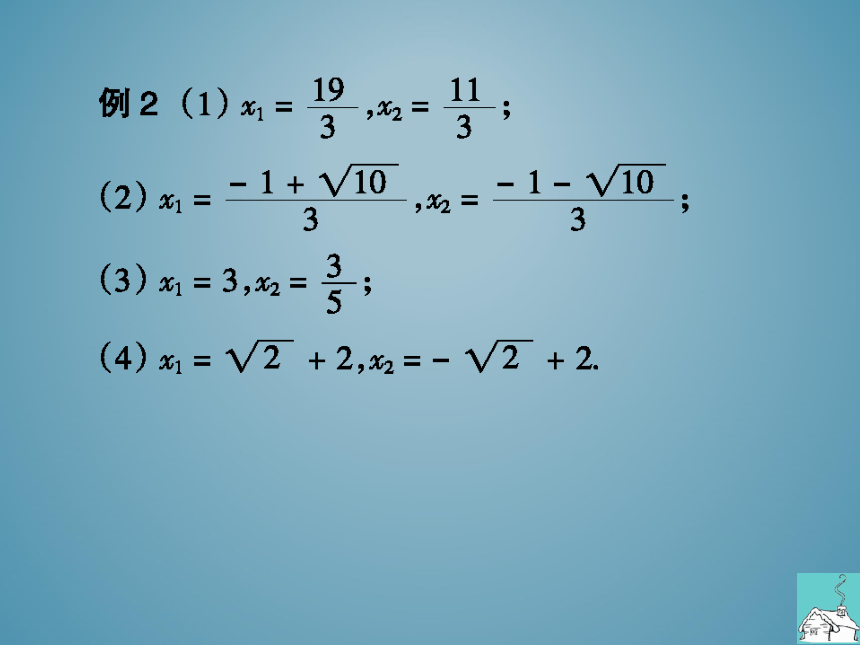

文档简介
(共16张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第4课时 因式分解法
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
C
D
D
五、考题链接
A
A
(一)学习目标
会用因式分解法解元二次方程,能够根据一元
二次方程的特点选择恰当的方法解方程
(二)课前预习
【检测1】关于x的元二次方程(x+3)(x-1)=0
的根是
检测2】一元二次方程x2-16=0的根是
★用因式分解法解一元二次方程
例1解下列方程:
(1)3x2+2x=0;
(2)16(2x-1)2=25(x-2)2
分析:(1)可化为x(3x+2)=0;(2)先移项,再用
平方差公式分解因式,进而求解
例1(1)x=0,x2=
2:(2)x1=13
14
变式1(1)x1=-2,a=3;(2)x1=0,x2=-6
变式通
解下列方程
(1)(x-1)(x+2)=2(x+2);
(2)x2-6x+9=(2x+3)2
★用适当的方法解一元二次方程
例2用适当的方法解下列方程:
(1)9(x-5)2=16
(2)3x2+2x-3=0
(3)(x-3)2+4x(x-3)=0
(4)x2-4x+2=0.
分析:(1)直接开平方求解即可;(2)适合用公式
法;(3)有公因式,适合用因式分解法;(4)容易配方,
用配方法解比较筒便
例2(1)x=19,2=1;
(2)x1=
1+V10
1-V10
(3)x1=3,x2
3
(4)x1=V2+2,‰=-V2+2
变式2
我们经学习了一元二次方程的三种解法:因式
分解法、配方法和公式法.请从以下一元二次方程中
任选一个,并选择你认为适当的方法解这个方程
(1)x2-3x+1=0
(2)(x-1)2=3;
(3)x2-3x=0.
变式2(1)x=3+5,=3-V5
2
(2)x1=1+V3,x2=1-V3;
(3)x1=0,x2=3
用因式分解法解元二次方程,要使方程一边
为两个
因式相乘,另一边为
再分
别使各一次因式等于_,从而实现降次
适用于所有一元二次方程,
用于某些元二次方程.总之,解一元二
次方程的基本思路是:将二次方程化为一次方程,即
降次
A组基础练习
1.一元二次方程x2+3x=0的解是
x
B.x1=0,x2=3
C.x1=0,x2=-3
D.‰2=3
2.方程(x-5)(x-6)=x-5的解是().
A.x=5
B.x1=5,x2=6
D.x1=5
3.方程x2-4x=0的解是_
4.若关于x的一元二次方程mx2-(2m-3)x+
2m-3=0有两个相等的实数根,则m的值为
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第4课时 因式分解法
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
C
D
D
五、考题链接
A
A
(一)学习目标
会用因式分解法解元二次方程,能够根据一元
二次方程的特点选择恰当的方法解方程
(二)课前预习
【检测1】关于x的元二次方程(x+3)(x-1)=0
的根是
检测2】一元二次方程x2-16=0的根是
★用因式分解法解一元二次方程
例1解下列方程:
(1)3x2+2x=0;
(2)16(2x-1)2=25(x-2)2
分析:(1)可化为x(3x+2)=0;(2)先移项,再用
平方差公式分解因式,进而求解
例1(1)x=0,x2=
2:(2)x1=13
14
变式1(1)x1=-2,a=3;(2)x1=0,x2=-6
变式通
解下列方程
(1)(x-1)(x+2)=2(x+2);
(2)x2-6x+9=(2x+3)2
★用适当的方法解一元二次方程
例2用适当的方法解下列方程:
(1)9(x-5)2=16
(2)3x2+2x-3=0
(3)(x-3)2+4x(x-3)=0
(4)x2-4x+2=0.
分析:(1)直接开平方求解即可;(2)适合用公式
法;(3)有公因式,适合用因式分解法;(4)容易配方,
用配方法解比较筒便
例2(1)x=19,2=1;
(2)x1=
1+V10
1-V10
(3)x1=3,x2
3
(4)x1=V2+2,‰=-V2+2
变式2
我们经学习了一元二次方程的三种解法:因式
分解法、配方法和公式法.请从以下一元二次方程中
任选一个,并选择你认为适当的方法解这个方程
(1)x2-3x+1=0
(2)(x-1)2=3;
(3)x2-3x=0.
变式2(1)x=3+5,=3-V5
2
(2)x1=1+V3,x2=1-V3;
(3)x1=0,x2=3
用因式分解法解元二次方程,要使方程一边
为两个
因式相乘,另一边为
再分
别使各一次因式等于_,从而实现降次
适用于所有一元二次方程,
用于某些元二次方程.总之,解一元二
次方程的基本思路是:将二次方程化为一次方程,即
降次
A组基础练习
1.一元二次方程x2+3x=0的解是
x
B.x1=0,x2=3
C.x1=0,x2=-3
D.‰2=3
2.方程(x-5)(x-6)=x-5的解是().
A.x=5
B.x1=5,x2=6
D.x1=5
3.方程x2-4x=0的解是_
4.若关于x的一元二次方程mx2-(2m-3)x+
2m-3=0有两个相等的实数根,则m的值为
同课章节目录
