18第二十二章 实际问题与一元二次方程(2)
文档属性
| 名称 | 18第二十二章 实际问题与一元二次方程(2) |  | |
| 格式 | zip | ||
| 文件大小 | 724.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:46:07 | ||
图片预览








文档简介
(共26张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第8课时 实际问题与一元二次方程(2)
一、新课导入
D
二、典型问题
三、归纳小结
四、阶梯训练
B
A
A
五、考题链接
(一)学习目标
1.熟练利用面积建立一元二次方程的数学模型,
并运用它解决实际问题.
2.能够结合实际情况正确处理一元二次方程根
的取舍问题
3.熟练掌握列方程解应用题的步骤和关键
(二)课前预习
【检测1】从正方形铁片上截去2cm宽的一个
长方形,余下部分的面积是48cm2,则原来的正方形
铁片的面积是
A.8 cm
B. 16 cm2
C8 cm
D. 64 cm2
检测2】一个知形的长比宽多4cm,面积是96cm2,
若设矩形的宽为xcm,则可得方程
★平面图形的面积问题
例1某市为打造“绿色家园,宜居城市”,在一块
长80m宽60m的矩形场地中开胖出一个矩形花园,
使四周留下的道路宽度一样,并且矩形花园的面积是
原矩形场地的一半.求道路宽为多少
分析:分别表示出矩形花园的长、宽、面积和原矩
形场地的面积,然后根据“矩形花园的面积是原矩形
场地的一半”这一等量关系列出方程,解答即可
例1设道路宽是xm,根据题意,得
2(80-2x)(60-2x)=80×60
整理,得x2-70x+600=0.
1,b=-70,c=600,
b2-4ac=(-70)2-4×1×600=2500>0
70±V2500
,三
=35±25,
即x1=60(不合题意,舍去),x2=10
答:道路的宽度是10m
变式1
如图1所示,某村计划建造矩形蔬菜温室,要求
长与宽的比为2:1,在温室内,沿前侧内墙保留3m
宽的空地,其他三侧内墙各保留1m宽的通道,当矩
形温室的长与宽为多少时,蔬菜种植区域的面积为
288m2
前
蔬菜种植区
地
图1
变式1设长为2xm,宽为xm,则蔬菜种植区域长为
(2x-4)m,宽为(x-2)m
根据题意,得(2x-4)(x-2)=288
整理,得2x2-8x-280=0.
解得x1=14,x2=-10(不合题意,舍去)
答;温室长为28m,宽为14m
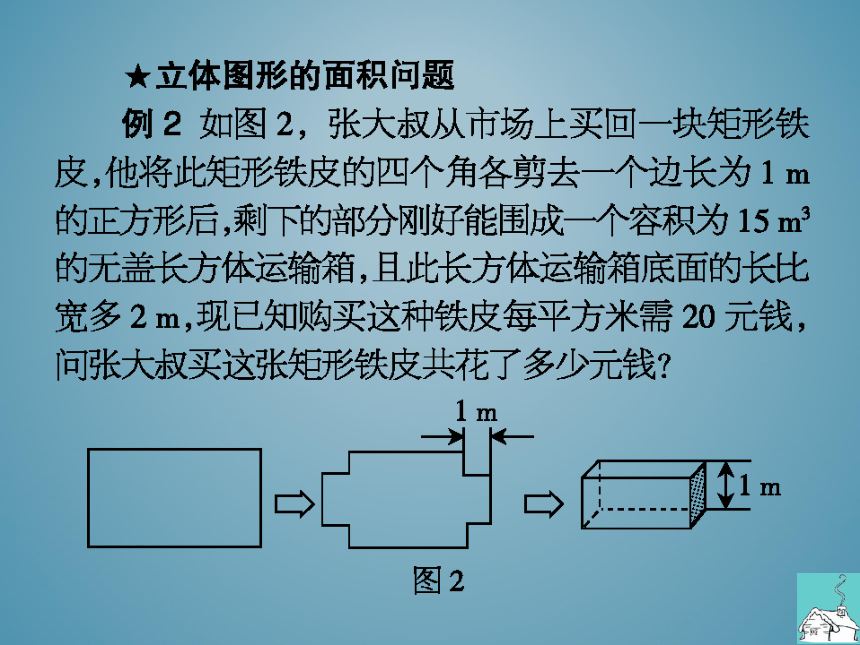
★立体图形的面积问题
例2如图2,张大叔从市场上买回一块矩形铁
皮,他将此矩形铁皮的四个角各剪去一个边长为1m
的正方形后,剩下的部分刚好能围成一个容积为15m3
的无盖长方体运输箱,且此长方体运输箱底面的长比
宽多2m,现已知购买这种铁皮每平方米需20元钱,
问张大叔买这张矩形铁皮共花了多少元钱
图2
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第8课时 实际问题与一元二次方程(2)
一、新课导入
D
二、典型问题
三、归纳小结
四、阶梯训练
B
A
A
五、考题链接
(一)学习目标
1.熟练利用面积建立一元二次方程的数学模型,
并运用它解决实际问题.
2.能够结合实际情况正确处理一元二次方程根
的取舍问题
3.熟练掌握列方程解应用题的步骤和关键
(二)课前预习
【检测1】从正方形铁片上截去2cm宽的一个
长方形,余下部分的面积是48cm2,则原来的正方形
铁片的面积是
A.8 cm
B. 16 cm2
C8 cm
D. 64 cm2
检测2】一个知形的长比宽多4cm,面积是96cm2,
若设矩形的宽为xcm,则可得方程
★平面图形的面积问题
例1某市为打造“绿色家园,宜居城市”,在一块
长80m宽60m的矩形场地中开胖出一个矩形花园,
使四周留下的道路宽度一样,并且矩形花园的面积是
原矩形场地的一半.求道路宽为多少
分析:分别表示出矩形花园的长、宽、面积和原矩
形场地的面积,然后根据“矩形花园的面积是原矩形
场地的一半”这一等量关系列出方程,解答即可
例1设道路宽是xm,根据题意,得
2(80-2x)(60-2x)=80×60
整理,得x2-70x+600=0.
1,b=-70,c=600,
b2-4ac=(-70)2-4×1×600=2500>0
70±V2500
,三
=35±25,
即x1=60(不合题意,舍去),x2=10
答:道路的宽度是10m
变式1
如图1所示,某村计划建造矩形蔬菜温室,要求
长与宽的比为2:1,在温室内,沿前侧内墙保留3m
宽的空地,其他三侧内墙各保留1m宽的通道,当矩
形温室的长与宽为多少时,蔬菜种植区域的面积为
288m2
前
蔬菜种植区
地
图1
变式1设长为2xm,宽为xm,则蔬菜种植区域长为
(2x-4)m,宽为(x-2)m
根据题意,得(2x-4)(x-2)=288
整理,得2x2-8x-280=0.
解得x1=14,x2=-10(不合题意,舍去)
答;温室长为28m,宽为14m
★立体图形的面积问题
例2如图2,张大叔从市场上买回一块矩形铁
皮,他将此矩形铁皮的四个角各剪去一个边长为1m
的正方形后,剩下的部分刚好能围成一个容积为15m3
的无盖长方体运输箱,且此长方体运输箱底面的长比
宽多2m,现已知购买这种铁皮每平方米需20元钱,
问张大叔买这张矩形铁皮共花了多少元钱
图2
同课章节目录
